MATH347: Linear algebra for applicationsMay 2, 2024

Solve the following problems (5 course points each). Present a brief motivation of your method of solution. Problems 9 and 10 are optional; attempt them if you wish to improve your midterm examination score.

1. Form the matrix product corresponding to the following linear combinations

   ${\displaystyle {𝒃}_1=x_1{𝒂}_1+x_2{𝒂}_2+\cdots +x_n{𝒂}_n,}$ ${\displaystyle {𝒃}_2=y_1{𝒂}_1+y_2{𝒂}_2+\cdots +y_n{𝒂}_n,}$ ${\displaystyle {𝒃}_3=z_1{𝒂}_1+z_2{𝒂}_2+\cdots +z_n{𝒂}_n.}$

   Specify all matrix dimensions and column vectors.

   Solution. Consider ${𝒂}_1\in {ℝ}^m$. Consistency of vector addition then implies ${𝒂}_2,\dots ,{𝒂}_n,{𝒃}_1,{𝒃}_2,{𝒃}_3\in {ℝ}^m$. Form

   ${\displaystyle 𝑩=\left[\begin{array}{lll}{𝒃}_1& {𝒃}_2& {𝒃}_3\end{array}\right]=𝑨𝑪\in {ℝ}^{m\times p},p=3.}$

   The vectors entering into the linear combinations are

   ${\displaystyle 𝑨=\left[\begin{array}{llll}{𝒂}_1& {𝒂}_2& \dots & {𝒂}_n\end{array}\right]\in {ℝ}^{m\times n}.}$

   The scaling coefficients of the three linear combinations are

   ${\displaystyle 𝑪=\left[\begin{array}{lll}{𝒄}_1& {𝒄}_2& {𝒄}_3\end{array}\right]=\left[\begin{array}{lll}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ ⋮& ⋮& ⋮\\ x_n& y_n& z_n\end{array}\right]\in {ℝ}^{n\times p},p=3.}$

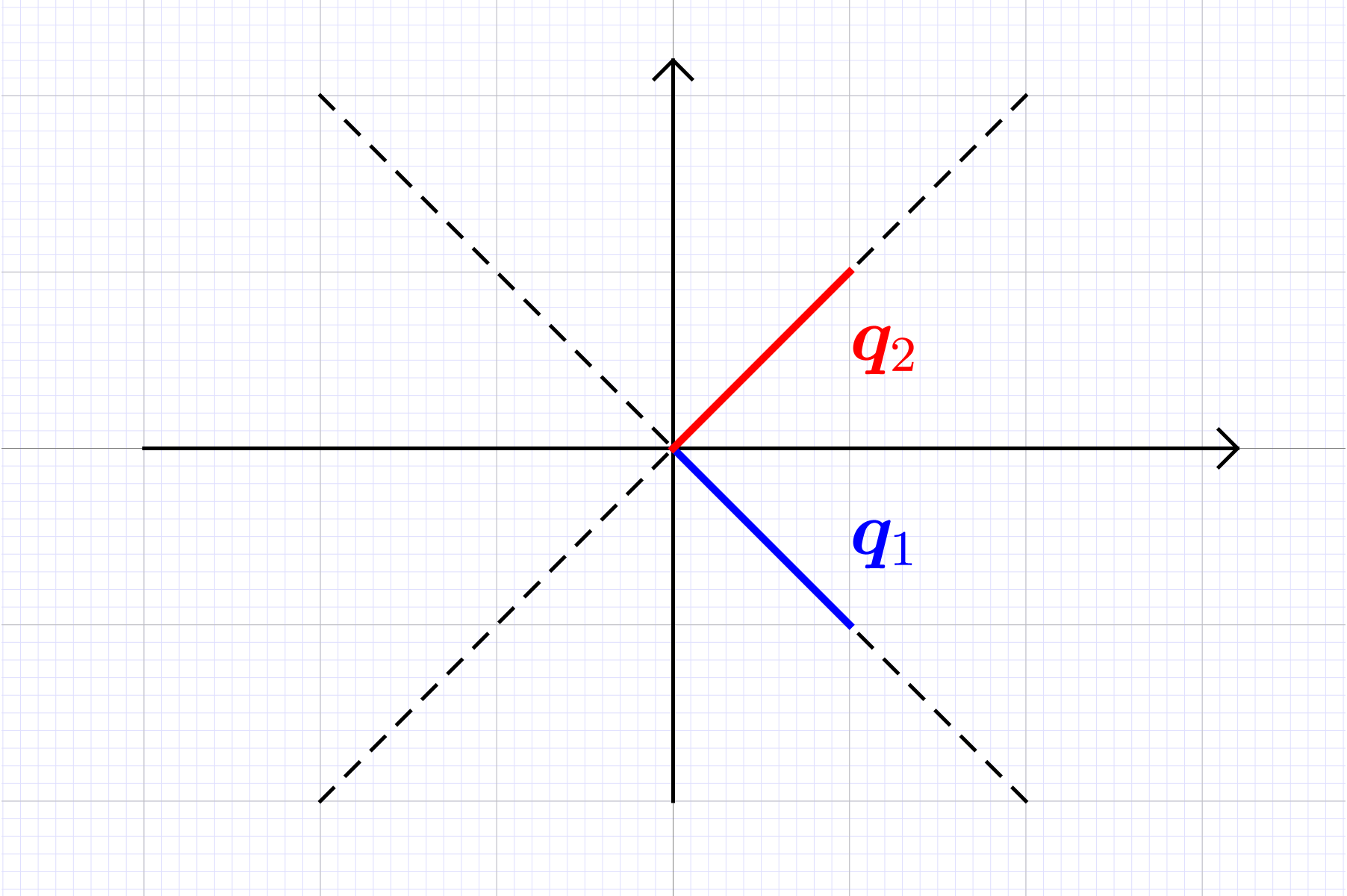
2. For $𝑨\in {ℝ}^{m\times m}$ let $𝒃=𝑨𝒙$ and $𝒚\ne 𝟎$ be a solution of the linear system ${𝑨}^T𝒚=𝟎$. Compute the angle between $𝒃$ and $𝒚$.

   Solution. From $𝒃=𝑨𝒙$ deduce $𝒃\in C\left(𝑨\right)$. From ${𝑨}^T𝒚=𝟎$, deduce that $𝒚\in N\left({𝑨}^T\right)$. The FTLA states $C\left(𝑨\right)\perp N\left({𝑨}^T\right)$, hence $𝒃\perp 𝒚$, and the angle between the two vectors is $\theta =\pi /2$ (orthogonal).

3. With $𝑸\in {ℝ}^{m\times m}$ known to be orthogonal, carry out the following block matrix multiplication. Identify dimensions of all blocks, and the blocks and the dimensions of the resulting $𝑪$ matrix

   ${\displaystyle 𝑪=\left[\begin{array}{ll}𝑸& 𝑰\\ 𝟎& 𝑸\end{array}\right]\left[\begin{array}{ll}𝑨& 𝑰\\ 𝟎& 𝑨\end{array}\right]{\left[\begin{array}{ll}𝑸& 𝑰\\ 𝟎& 𝑸\end{array}\right]}^T.}$

   Solution. Consistency of multiplication requires $𝑰,𝟎\in {ℝ}^{m\times m}$, thereby leading to $𝑪\in {ℝ}^{2m\times 2m}$. Apply “row-over-columns” for matrix blocks, noting that ${𝑰}^T=𝑰$, ${𝟎}^T=𝟎$, $𝑸{𝑸}^T=𝑰$

   ${\displaystyle 𝑪=\left[\begin{array}{ll}𝑸& 𝑰\\ 𝟎& 𝑸\end{array}\right]\left[\begin{array}{ll}𝑨& 𝑰\\ 𝟎& 𝑨\end{array}\right]\left[\begin{array}{ll}{𝑸}^T& 𝟎\\ 𝑰& {𝑸}^T\end{array}\right]=\left[\begin{array}{ll}𝑸& 𝑰\\ 𝟎& 𝑸\end{array}\right]\left[\begin{array}{ll}𝑨{𝑸}^T+𝑰& {𝑸}^T\\ 𝑨& 𝑨{𝑸}^T\end{array}\right]=\left[\begin{array}{ll}𝑸𝑨{𝑸}^T+𝑸+𝑨& 𝑰+𝑨{𝑸}^T\\ 𝑸𝑨& 𝑸𝑨{𝑸}^T\end{array}\right].}$

4. Compute $𝒄={𝑨}^T𝒃$ and the projection of $𝒃$ onto $C\left(𝑨\right)$ for

   ${\displaystyle 𝑨=\left[\begin{array}{ll}2& 3\\ -1& 1\\ -1& 2\\ -4& 0\end{array}\right],𝒃=\left[\begin{array}{l}1\\ -1\\ -1\\ 1\end{array}\right].}$

   Solution. Apply “row-over-columns” rule to obtain

   ${\displaystyle 𝒄={\left[\begin{array}{ll}2& 3\\ -1& 1\\ -1& 2\\ -4& 0\end{array}\right]}^T\left[\begin{array}{l}1\\ -1\\ -1\\ 1\end{array}\right]=\left[\begin{array}{llll}2& -1& -1& -4\\ 3& 1& 2& 0\end{array}\right]\left[\begin{array}{l}1\\ -1\\ -1\\ 1\end{array}\right]=\left[\begin{array}{l}0\\ 0\end{array}\right].}$

   The above implies $𝒃\in N\left({𝑨}^T\right)$, and by the FTLA the projection of $𝒃$ onto $C\left(𝑨\right)$ is the zero vector.

5. Find the $LU$ decomposition of

   ${\displaystyle 𝑨=\left[\begin{array}{lll}1& 1& 1\\ 2& 5& 5\\ 4& 9& 15\end{array}\right].}$

   Solution. Carry out reduction to upper triangular form, noting multipliers used in the process

   ${\displaystyle {𝑳}_1𝑨=\left[\begin{array}{lll}1& 0& 0\\ -2& 1& 0\\ -4& 0& 1\end{array}\right]\left[\begin{array}{lll}1& 1& 1\\ 2& 5& 5\\ 4& 9& 15\end{array}\right]=\left[\begin{array}{lll}1& 1& 1\\ 0& 3& 3\\ 0& 5& 11\end{array}\right].}$ ${\displaystyle {𝑳}_2{𝑳}_1𝑨=\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\\ 0& -5/3& 1\end{array}\right]\left[\begin{array}{lll}1& 1& 1\\ 0& 3& 3\\ 0& 5& 11\end{array}\right]=\left[\begin{array}{lll}1& 1& 1\\ 0& 3& 3\\ 0& 0& 6\end{array}\right]=𝑼.}$

   Find $𝑨={𝑳}_1^{-1}{𝑳}_2^{-1}𝑼=𝑳𝑼$. Compute

   ${\displaystyle 𝑳={𝑳}_1^{-1}{𝑳}_2^{-1}=\left[\begin{array}{lll}1& 0& 0\\ 2& 1& 0\\ 4& 0& 1\end{array}\right]\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\\ 0& 5/3& 1\end{array}\right]=\left[\begin{array}{lll}1& 0& 0\\ 2& 1& 0\\ 4& 5/3& 1\end{array}\right].}$

   Verify

   ${\displaystyle 𝑳𝑼=\left[\begin{array}{lll}1& 0& 0\\ 2& 1& 0\\ 4& 5/3& 1\end{array}\right]\left[\begin{array}{lll}1& 1& 1\\ 0& 3& 3\\ 0& 0& 6\end{array}\right]=\left[\begin{array}{lll}1& 1& 1\\ 2& 5& 5\\ 4& 9& 15\end{array}\right].?}$

6. State the eigenvalues and eigenvectors of $𝑪=𝑩𝑨,𝑨,𝑩\in {ℝ}^{2\times 2}$, with $𝑪$ the matrix describing: (a) rotation by $\theta =\pi /2$ ($𝑨$ matrix) followed by reflection across the $x_1$ axis ($𝑩$ matrix).

   Solution. Let $𝒚=𝑨𝒒$, $𝒛=𝑩𝒚=𝑪𝒒$. From sketch below, note that ${𝒒}_1={\left[\begin{array}{ll}1& -1\end{array}\right]}^T$ rotated by $\pi /2$ becomes ${𝒚}_1=$${\left[\begin{array}{ll}1& 1\end{array}\right]}^T$, which when reflected acorss the horizontal axis is again ${𝒒}_1={\left[\begin{array}{ll}1& -1\end{array}\right]}^T$, thus an eigenvector with associated eigenvalue ${\lambda }_1=1$. Similarly, vector ${𝒒}_2={\left[\begin{array}{ll}1& 1\end{array}\right]}^T$ rotated by $\pi /2$ becomes ${𝒚}_2=$${\left[\begin{array}{ll}-1& 1\end{array}\right]}^T$, which when reflected acorss the horizontal axis is ${\left[\begin{array}{ll}-1& -1\end{array}\right]}^T=-{𝒒}_2$, thus an eigenvector with eigenvalue ${\lambda }_2=-1$.

   Figure 1.

7. Compute the eigendecomposition of

   ${\displaystyle 𝑨=\left[\begin{array}{ll}1& 1\\ 1& 1\end{array}\right].}$

   Solution. The characteristic polynomial is

   ${\displaystyle p\left(\lambda \right)=\det (\lambda 𝑰-𝑨)=\left|\begin{array}{ll}\lambda -1& -1\\ -1& \lambda -1\end{array}\right|=\lambda (\lambda -2),}$

   with resulting eigenvalues ${\lambda }_1=0$, ${\lambda }_2=2_{}$. For ${\lambda }_1=0$ perform row reduction to find eigenvector ${𝒙}_1$

   ${\displaystyle 𝑨-{\lambda }_1𝑰=\left[\begin{array}{ll}1& 1\\ 1& 1\end{array}\right]\sim \left[\begin{array}{ll}1& 1\\ 0& 0\end{array}\right]\Rightarrow {𝒙}_1=\left[\begin{array}{l}1\\ -1\end{array}\right],{𝒒}_1={𝒙}_1/||{𝒙}_1||=\frac{1}{\sqrt{2}}\left[\begin{array}{l}1\\ -1\end{array}\right].}$

   Similarly, for ${\lambda }_2=2$

   ${\displaystyle 𝑨-{\lambda }_2𝑰=\left[\begin{array}{ll}-1& 1\\ 1& -1\end{array}\right]\sim \left[\begin{array}{ll}-1& 1\\ 0& 0\end{array}\right]\Rightarrow {𝒙}_2=\left[\begin{array}{l}1\\ 1\end{array}\right],{𝒒}_2={𝒙}_2/||{𝒙}_2||=\frac{1}{\sqrt{2}}\left[\begin{array}{l}1\\ 1\end{array}\right].}$

   Since $𝑨={𝑨}^T$, the eigendecomposition exists and is orthogonal

   ${\displaystyle 𝑨=𝑸𝚲{𝑸}^T=\frac{1}{\sqrt{2}}\left[\begin{array}{ll}1& 1\\ -1& 1\end{array}\right]\left[\begin{array}{ll}0& 0\\ 0& 2\end{array}\right]\frac{1}{\sqrt{2}}\left[\begin{array}{ll}1& -1\\ 1& 1\end{array}\right].}$

8. Find the SVD of

   ${\displaystyle 𝑨=\left[\begin{array}{ll}4& 0\\ 4& 0\end{array}\right].}$

   Solution. Recall SVD $𝑨=𝑼𝚺{𝑽}^T$, with $𝑨,𝚺\in {ℝ}^{m\times n}$, $𝑼\in {ℝ}^{m\times m}$ orthogonal, $𝑽\in {ℝ}^{n\times n}$ orthogonal. For this problem $m=n=2$. Further recall $𝑼=\left[\begin{array}{llllll}{𝒖}_1& \dots & {𝒖}_r& {𝒖}_{r+1}& \dots & {𝒖}_m\end{array}\right],$$𝑽=\left[\begin{array}{llllll}{𝒗}_1& \dots & {𝒗}_r& {𝒗}_{r+1}& \dots & {𝒗}_n\end{array}\right]$. The matrix $𝑨$ has rank $r=1$, and ${𝒖}_1$ can be taken as

   ${\displaystyle {𝒖}_1=\frac{1}{\sqrt{2}}\left[\begin{array}{l}1\\ 1\end{array}\right].}$

   Since $𝑼$ is orthogonal take

   ${\displaystyle {𝒖}_2=\frac{1}{\sqrt{2}}\left[\begin{array}{l}1\\ -1\end{array}\right],}$

   to obtain

   ${\displaystyle 𝑼=\frac{1}{\sqrt{2}}\left[\begin{array}{ll}1& 1\\ 1& -1\end{array}\right].}$

   Take $𝑽=𝑰$ to obtain

   ${\displaystyle 𝑨𝑽=𝑨=𝑼𝚺\Rightarrow \left[\begin{array}{ll}4& 0\\ 4& 0\end{array}\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{ll}1& 1\\ 1& -1\end{array}\right]\left[\begin{array}{ll}{\sigma }_1& 0\\ 0& 0\end{array}\right]=\left[\begin{array}{ll}{\sigma }_1/\sqrt{2}& 0\\ {\sigma }_1/\sqrt{2}& 0\end{array}\right].}$

   Deduce that ${\sigma }_1=4\sqrt{2}$, completing the SVD.

9. Form the matrices $𝑨,𝑩\in {ℝ}^{2\times 2}$, $𝑪=𝑩𝑨,$ where $𝑪$ is the matrix describing: (a) rotation by $\theta =\pi /2$ ($𝑨$ matrix) followed by reflection across the $x_1$ axis ($𝑩$ matrix).

   Solution. The matrices are

   ${\displaystyle 𝑨=\left[\begin{array}{ll}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]=\left[\begin{array}{ll}0& -1\\ 1& 0\end{array}\right],𝑩=\left[\begin{array}{ll}1& 0\\ 0& -1\end{array}\right],𝑪=\left[\begin{array}{ll}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{ll}0& -1\\ 1& 0\end{array}\right]=\left[\begin{array}{ll}0& -1\\ -1& 0\end{array}\right].}$

10. Find bases for the four fundamental spaces of

    ${\displaystyle 𝑨=\left[\begin{array}{llll}1& 2& 3& 4\\ 2& -1& -1& -4\\ 3& 1& 2& 0\end{array}\right].}$

    Solution. Note that $𝑨\in {ℝ}^{m\times n}$ with $m=3$, $n=4$. Carry out row reduction

    ${\displaystyle 𝑨\sim \left[\begin{array}{llll}1& 2& 3& 4\\ 0& -5& -7& -12\\ 0& -5& -7& -12\end{array}\right]\sim \left[\begin{array}{llll}1& 2& 3& 4\\ 0& -5& -7& -12\\ 0& 0& 0& 0\end{array}\right],}$

    to find $r=\mathrm{rank}\left(𝑨\right)=2$.

    $C\left(𝑨\right)$: FTLA states $\dim C\left(𝑨\right)=r=2$. Take $r=2$ linearly independent columns as the basis, e.g.,

    ${\displaystyle \{\left[\begin{array}{l}1\\ 2\\ 3\end{array}\right],\left[\begin{array}{l}2\\ -1\\ 1\end{array}\right]\}.}$

    $C\left({𝑨}^T\right)$: FTLA states $\dim C\left({𝑨}^T\right)=r=2$. Take $r=2$ linearly independent rows as the basis, e.g.,

    ${\displaystyle \{\left[\begin{array}{l}1\\ 2\\ 3\\ 4\end{array}\right],\left[\begin{array}{l}2\\ -1\\ -1\\ -4\end{array}\right]\}.}$

    $N\left({𝑨}^T\right)$: FTLA states $\dim N\left({𝑨}^T\right)=m-r=1$. From row reduction of ${𝑨}^T$

    ${\displaystyle {𝑨}^T=\left[\begin{array}{lll}1& 2& 3\\ 2& -1& 1\\ 3& -1& 2\\ 4& -4& 0\end{array}\right]\sim \left[\begin{array}{lll}1& 2& 3\\ 0& -5& -5\\ 0& -7& -7\\ 0& -12& -12\end{array}\right]\sim \left[\begin{array}{lll}1& 2& 3\\ 0& 1& 1\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],}$

    consider system

    ${\displaystyle \{\begin{array}{l}{x}_1+2x_2+3x_3=0\\ x_2+x_3=0\end{array}..}$

    Take $x_3=\lambda$ as a free parameter to obtain

    ${\displaystyle \{\begin{array}{l}{x}_1+2x_2=-3\lambda \\ x_2=-\lambda \end{array}.,x_1=x_2=-\lambda .}$

    A basis vector for $N\left({𝑨}^T\right)$ is therefore

    ${\displaystyle \left\{\left[\begin{array}{l}1\\ 1\\ -1\end{array}\right]\right\}.}$

    Verify

    ${\displaystyle \left[\begin{array}{lll}1& 2& 3\\ 2& -1& 1\\ 3& -1& 2\\ 4& -4& 0\end{array}\right]\left[\begin{array}{l}1\\ 1\\ -1\end{array}\right]=\left[\begin{array}{l}0\\ 0\\ 0\\ 0\end{array}\right]?.}$

    $N\left(𝑨\right):$ FTLA states $\dim N\left(𝑨\right)=n-r=2$. Continue above row reduction of $𝑨$ to obtain reduced row echelon form

    ${\displaystyle 𝑨\sim \left[\begin{array}{llll}1& 2& 3& 4\\ 0& -5& -7& -12\\ 0& 0& 0& 0\end{array}\right]\sim \left[\begin{array}{llll}1& 2& 3& 4\\ 0& 1& 7/5& 12/5\\ 0& 0& 0& 0\end{array}\right]\sim \left[\begin{array}{llll}1& 0& 1/5& -4/5\\ 0& 1& 7/5& 12/5\\ 0& 0& 0& 0\end{array}\right]}$

    and form system

    ${\displaystyle \{\begin{array}{l}5x_1+x_3-4x_4=0\\ 5x_2+7x_3+12x_4=0\end{array}..}$

    Consider $x_3=\lambda$, $x_4=\mu$ to be free parameters to obtain

    ${\displaystyle \{\begin{array}{l}{x}_1=-(\lambda -4\mu )/5\\ x_2=-(7\lambda +12\mu )/5\end{array}..}$

    For $x_4=\mu =0$ obtain

    ${\displaystyle x_1=-\frac{1}{5}\lambda ,x_2=-\frac{7}{5}\lambda ,x_3=\lambda ,x_4=0,}$

    For $x_3=\lambda =0$ obtain

    ${\displaystyle x_1=\frac{4}{5}\mu ,x_2=-\frac{12}{5}\mu ,x_3=0,x_4=\mu .}$

    Deduce that a basis set for $N\left(𝑨\right)$ is

    ${\displaystyle \{\left[\begin{array}{l}-1\\ -7\\ 5\\ 0\end{array}\right],\left[\begin{array}{l}4\\ -12\\ 0\\ 5\end{array}\right]\}.}$

    Verify

    ${\displaystyle \left[\begin{array}{llll}1& 2& 3& 4\\ 2& -1& -1& -4\\ 3& 1& 2& 0\end{array}\right]\left[\begin{array}{ll}-1& 4\\ -7& -12\\ 5& 0\\ 0& 5\end{array}\right]=\left[\begin{array}{ll}0& 0\\ 0& 0\\ 0& 0\end{array}\right]?}$