MATH347

MATH347 L3: Matrix operations

New concepts:
- Matrix addition and scaling
- Matrix multiplication
- Matrix addition properties
- Matrix multiplication properties

Matrix addition

Definition. The sum of matrices $𝑨, 𝑩 \in ℝ^{m \times n}$

$𝑨 = [a_{i, j}], 𝑩 = [b_{i, j}]$

is the matrix $𝑪 = 𝑨 + 𝑩$ with components

$𝑪 = [c_{i, j}], c_{i, j} = a_{i, j} + b_{i, j}$

>>	A=[1 0 1; 2 -1 3]; B=[2 1 -1; 1 1 -1]; C=A+B; disp(A)

1 0 1 2 -1 3

>>

disp(B)

2 1 -1 1 1 -1

>>

A+B

$(\begin{array}{ccc} 3 & 1 & 0.0 \\ 3 & 0.0 & 2 \end{array})$

Matrix scaling

Definition. The scalar multiplication of matrix $𝑨 \in ℝ^{m \times n}$ by $α \in ℝ$ is $𝑩 = α 𝑨$

$𝑨 = [a_{i, j}], 𝑩 = [b_{i, j}] = [α a_{i, j}]$

>>	A=[1 0 1; 2 -1 3]; disp(A)

1 0 1 2 -1 3

>>

2*A

$(\begin{array}{ccc} 2 & 0.0 & 2 \\ 4 & - 2 & 6 \end{array})$

>>

A+A

$(\begin{array}{ccc} 2 & 0.0 & 2 \\ 4 & - 2 & 6 \end{array})$

>>

Matrix multiplication

Definition. Consider matrices $𝑨 = [\begin{array}{lll} 𝒂_{1} & \dots & 𝒂_{n} \end{array}] \in ℝ^{m \times n}$ , and $𝑿 = [\begin{array}{lll} 𝒙_{1} & \dots & 𝒙_{p} \end{array}] \in ℝ^{n \times p} .$ The matrix product $𝑩 = 𝑨 𝑿$ is a matrix $𝑩 = [\begin{array}{lll} 𝒃_{1} & \dots & 𝒃_{p} \end{array}] \in ℝ^{m \times p}$ with column vectors given by the matrix vector products

$𝒃_{k} = 𝑨 𝒙_{k}, for k = 1, 2 \dots, p .$

A matrix-matrix product is simply a set of matrix-vector products, and hence expresses multiple linear combinations in a concise way.
The dimensions of the matrices must be compatible, the number of rows of $𝑿$ must equal the number of columns of $𝑨$ .
A matrix-vector product is a special case of a matrix-matrix product when $p = 1$ .
We often write $𝑩 = 𝑨 𝑿$ in terms of columns as
$[\begin{array}{lll} 𝒃_{1} & \dots & 𝒃_{p} \end{array}] = 𝑨 [\begin{array}{lll} 𝒙_{1} & \dots & 𝒙_{p} \end{array}] = [\begin{array}{lll} 𝑨 𝒙_{1} & \dots & 𝑨 𝒙_{p} \end{array}]$

Matrix multiplication example

>>	A=[1 0 3; 2 1 4; -1 0 3]; disp(A)

1 0 3 2 1 4 -1 0 3

>>	X=[1 -1 0; 1 1 1; 0 1 0]; disp(X)

1 -1 0 1 1 1 0 1 0

>>

A*X

$(\begin{array}{ccc} 1 & 2 & 0.0 \\ 3 & 3 & 1 \\ - 1 & 4 & 0.0 \end{array})$

>>	[AX(:,1) AX(:,2) A*X(:,3)]

$(\begin{array}{ccc} 1 & 2 & 0.0 \\ 3 & 3 & 1 \\ - 1 & 4 & 0.0 \end{array})$

Matrix multiplication: componentwise

Definition. Consider matrices $𝑨 = [\begin{array}{l} a_{i, j} \end{array}] \in ℝ^{m \times n}$ , and $𝑿 = [x_{i, j}] \in ℝ^{n \times p} .$ The matrix product $𝑩 = 𝑨 𝑿 = [b_{i, j}]$ is a matrix $𝑩 \in ℝ^{m \times p}$ with components

$b_{i, j} = a_{i, 1} x_{1, j} + a_{i, 2} x_{2, j} + \dots + a_{i, n} x_{n, j} = \sum_{k = 1}^{n} a_{i, k} x_{k, j}$

$𝑨 𝑿 = [\begin{array}{llll} a_{1, 1} & a_{1, 2} & \dots & a_{1, n} \\ a_{2, 1} & a_{2, 2} & \dots & a_{2, n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m, 1} & a_{m, 2} & a_{m, n} \end{array}] [\begin{array}{llll} x_{1, 1} & x_{1, 2} & \dots & x_{1, p} \\ x_{2, 1} & x_{2, 2} & \dots & x_{2, p} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ x_{n, 1} & x_{n, 2} & x_{n, p} \end{array}]$

$b_{2, 1} = a_{2, 1} x_{1, 1} + a_{2, 2} x_{2, 1} + \dots + a_{2, n} x_{n, 1}$

Matrix multiplication example revisited

>>	A=[1 0 3; 2 1 4; -1 0 3]; disp(A)

1 0 3 2 1 4 -1 0 3

>>	X=[1 -1 0; 1 1 1; 0 1 0]; disp(X)

1 -1 0 1 1 1 0 1 0

>>

A*X

$(\begin{array}{ccc} 1 & 2 & 0.0 \\ 3 & 3 & 1 \\ - 1 & 4 & 0.0 \end{array})$

>>	dot(A(1,:),X(:,2))

$2$

>>	dot(A(3,:),X(:,1))

$- 1$

Matrix addition properties compared to real numbers

$𝑨 \in ℝ^{m \times n}, 𝑩 \in ℝ^{m \times n}$ , $α, β, γ \in ℝ$
Associativity: $(α + β) + γ = α + (β + γ)$ , $(𝑨 + 𝑩) + 𝑪 = 𝑨 + (𝑩 + 𝑪)$
Zero element: $α + 0 = α$ , $𝑨 + 𝟎 = 𝑨$
$𝑨 = [\begin{array}{lll} 0 & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & 0 \end{array}]$
Opposite: $α + (- α) = α + (- 1) α = 0$ , $𝑨 + (- 𝑨) = 𝑨 + (- 1) 𝑨 = 𝟎 .$
Commutativity: $α + β = β + α$ , $𝑨 + 𝑩 = 𝑩 + 𝑨$

Matrix multiplication properties compared to real numbers

$𝑨 \in ℝ^{m \times n}, 𝑩 \in ℝ^{n \times p}, 𝑪 \in ℝ^{p \times q}$ , $α, β, γ \in ℝ$
Associativity: $(α β) γ = α (β γ)$ , $(𝑨 𝑩) 𝑪 = 𝑨 (𝑩 𝑪)$
Unity element: $α \cdot 1 = 1 \cdot α = α$ , $𝑨 𝑰 = 𝑰 𝑨 = 𝑨$ ( $𝑰$ is the identity matrix)
$𝑰 = [\begin{array}{llll} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & 1 \end{array}]$
Inverse: $α \neq 0$ , $α \cdot α^{- 1} = α^{- 1} \cdot α = 1$ , Would like $𝑨 𝑨^{- 1} = 𝑨^{- 1} 𝑨 = 𝑰$ , but need to establish conditions for existence of $𝑨^{- 1}$ (analogous to $α \neq 0$ )

Commutativity: $α β = β α$ . In general $𝑨 𝑩$ need not be equal to $𝑩 𝑨$ .

Dot product as matrix multiplication

Dot product of $𝒖, 𝒗 \in ℝ^{m}$ : $𝒖 \cdot 𝒗 = u_{1} v_{1} + \dots + u_{m} v_{m}$ is a matrix multiplication
$𝒖 \cdot 𝒗 = 𝒖^{T} 𝒗 = [\begin{array}{lll} u_{1} & \dots & u_{m} \end{array}] [\begin{array}{l} v_{1} \\ ⋮ \\ v_{m} \end{array}] = 𝒗^{T} 𝒖 = [\begin{array}{lll} v_{1} & \dots & v_{m} \end{array}] [\begin{array}{l} u_{1} \\ ⋮ \\ u_{m} \end{array}]$
The above form is useful in many cases, e.g., proving the cosine theorem

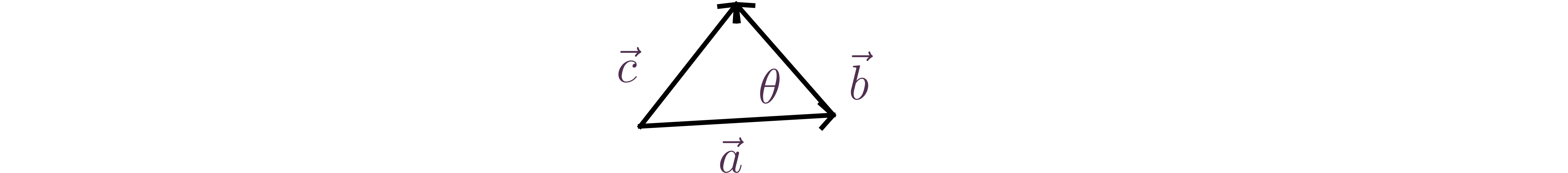
Cosine theorem: $\overset{⇀}{c} = \overset{⇀}{a} + \overset{⇀}{b}$ , $c^{2} = a^{2} + b^{2} - 2 a b \cos θ$ , with $a = || \overset{⇀}{a} ||$ , $b = || \overset{⇀}{b} ||$ , $c = || \overset{⇀}{c} ||$ .

$𝒄 = 𝒂 + 𝒃 \Rightarrow$ $𝒄^{T} = 𝒂^{T} + 𝒃^{T}$ , $𝒄^{T} 𝒄 = (𝒂^{T} + 𝒃^{T}) (𝒂 + 𝒃) \Rightarrow {|| 𝒄 ||}^{2} = {|| 𝒂^{} ||}^{2} + {|| 𝒃 ||}^{2} + 2 𝒂^{T} 𝒃$

${|| 𝒄 ||}^{2} = {|| 𝒂^{} ||}^{2} + {|| 𝒃 ||}^{2} + 2 || 𝒂 || ⫴ 𝒃 ⫴ \cos (π - θ) \Rightarrow$

{|| 𝒄 ||}^{2} = {|| 𝒂^{} ||}^{2} + {|| 𝒃 ||}^{2} - 2 || 𝒂 || || 𝒃 || \cos θ \Rightarrow c^{2} = a^{2} + b^{2} - 2 a b \cos θ .