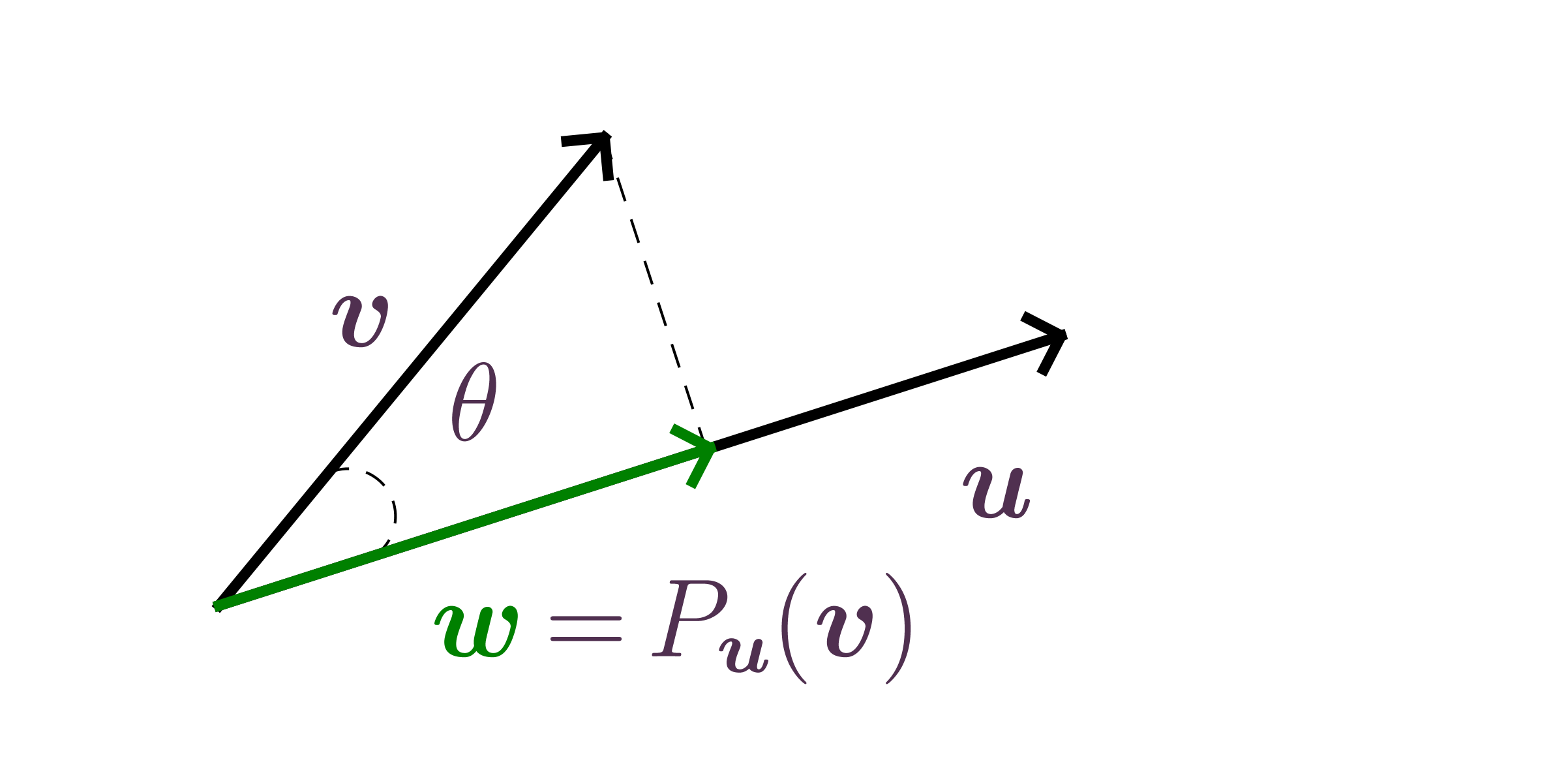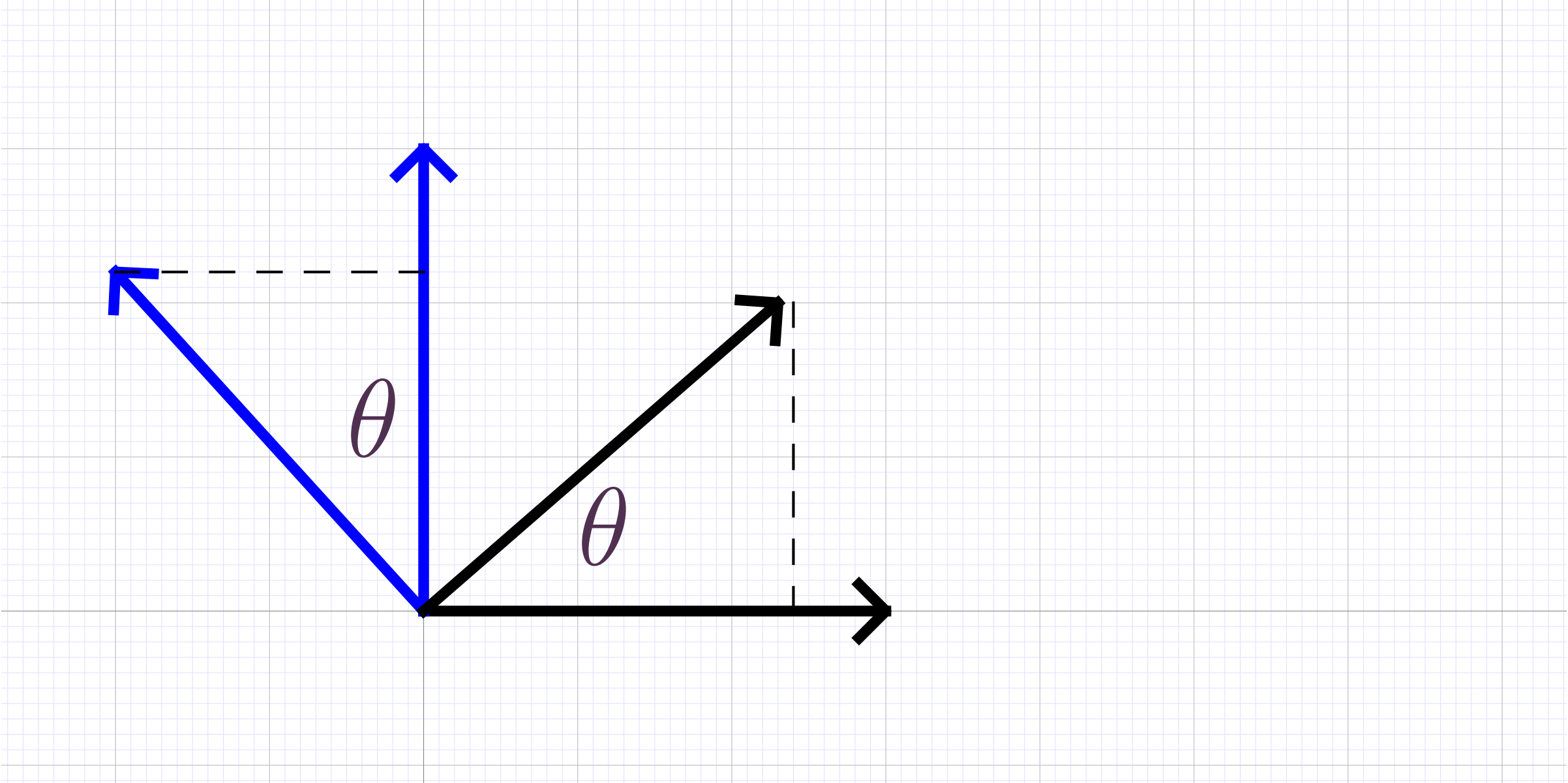MATH347

MATH347 L5: Linear transformations (mappings)

New concepts:
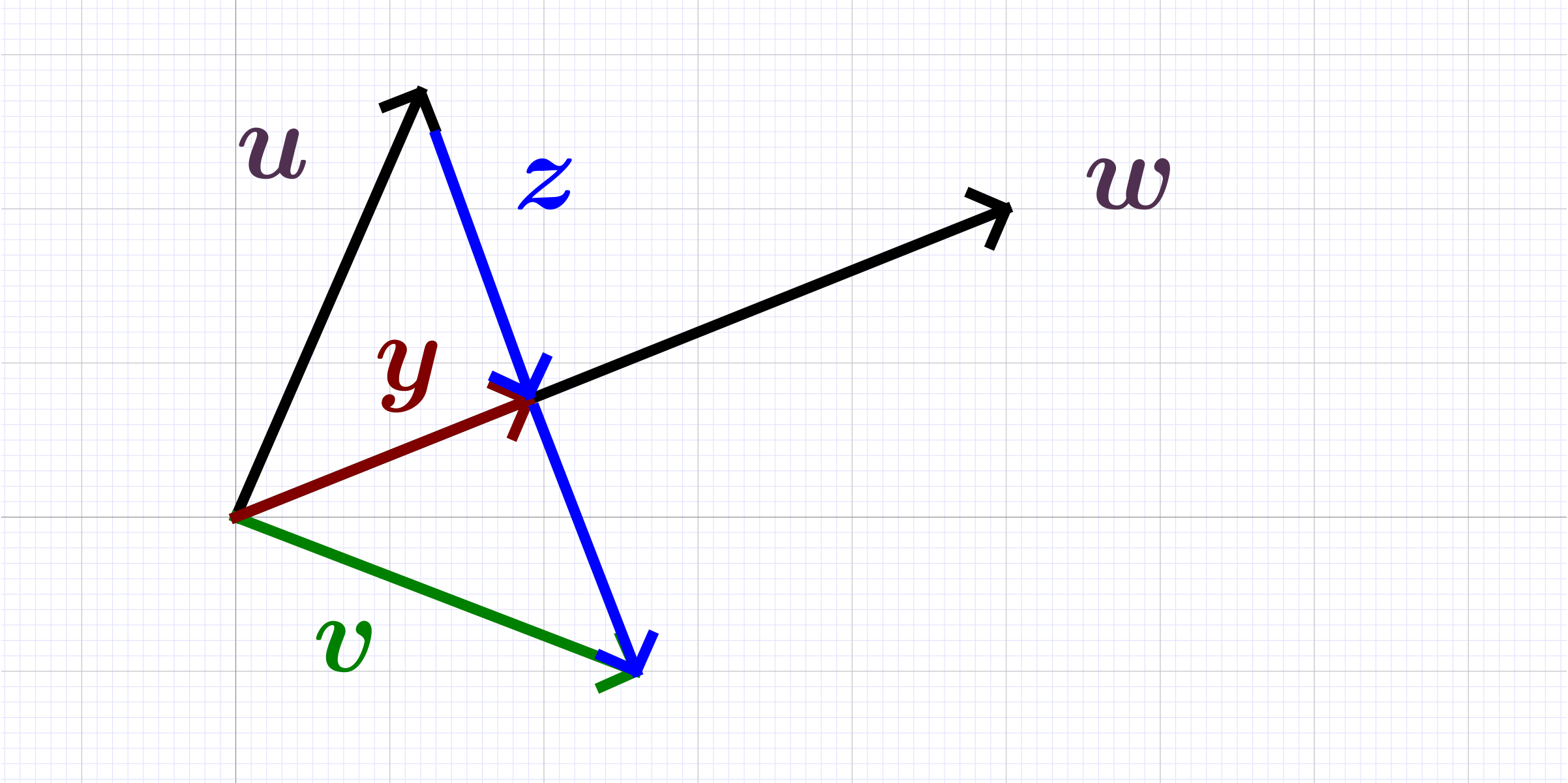
- Linear transformation
- Matrix of a linear transformation
- Common transformations: stretching, orthogonal projection, reflection, rotation
- Composition of linear transformations

Linear transformations (mappings)

Calculus studies $f : ℝ \to ℝ$ , functions defined on reals with values in reals
Linear algebra studies $T : ℝ^{n} \to ℝ^{m}$ , mapping of vectors in $ℝ^{n}$ to vectors in $ℝ^{m}$
Of special interest: mappings that preserve linear combinations
$T (α 𝒖 + β 𝒗) = α T (𝒖) + β T (𝒗)$
Such mappings are said to be linear.
Examples, counter-examples:
- $f : ℝ \to ℝ$ , $m = n = 1$ , $f (x) = a x$ is a linear mapping
  $f (α x + β y) = a (α x + β y) = α a x + α β y = α f (x) + β f (y)$
- $g : ℝ \to ℝ$ , $m = n = 1$ , $g (x) = a x + b$ is not a linear mapping
  $g (α x + β y) = a (α x + β y) + b = α a x + b + α β y = α g (x) + β g (y) - b$
- Matrix multiplication is linear $T : ℝ^{n} \to ℝ^{m}$ , $T (𝒙) = 𝑨 𝒙$ , $𝑨 \in ℝ^{m \times n}$
  $T (α 𝒙 + β 𝒚) = 𝑨 (α 𝒙 + β 𝒚) = α 𝑨 𝒙 + β 𝑨 𝒚 = α T (𝒙) + β T (𝒚)$
- $S : ℝ^{n} \to ℝ^{m}$ , $S (𝒙) = 𝑨 𝒙 + 𝒃$ is not a linear mapping

Matrix of a linear transformation

$𝒗 \in ℝ^{n}$ , $𝒗 = 𝑰 𝒗$ , $𝑰 = [\begin{array}{llll} 𝒆_{1} & 𝒆_{2} & \dots & 𝒆_{n} \end{array}]$
$𝒗 = [\begin{array}{llll} 𝒆_{1} & 𝒆_{2} & \dots & 𝒆_{n} \end{array}] [\begin{array}{l} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{array}] = v_{1} 𝒆_{1} + \dots + v_{n} 𝒆_{n} = v_{1} [\begin{array}{l} 1 \\ 0 \\ ⋮ \\ 0 \end{array}] + \dots + v_{n} [\begin{array}{l} 0 \\ ⋮ \\ 0 \\ 1 \end{array}]$
$T : ℝ^{n} \to ℝ^{m}$ a linear mapping (transformation)
$T (𝒗) = T (v_{1} 𝒆_{1} + \dots + v_{n} 𝒆_{n}) = v_{1} T (𝒆_{1}) + \dots + v_{n} T (𝒆_{n})$
Let $𝑨 = [\begin{array}{llll} T (𝒆_{1}) & T (𝒆_{2}) & \dots & T (𝒆_{n}) \end{array}] \in ℝ^{m \times n}$ , $T (𝒗) = 𝑨 𝒗$ . $𝑨$ is the standard matrix of a linear transformation

Stretching

$T$ stretches the $x$ component of $𝒗 \in ℝ^{2}$ by factor $α$ , the $y$ component by $β$
$T (𝒆_{1}) = [\begin{array}{l} α \\ 0 \end{array}], T (𝒆_{2}) = [\begin{array}{l} 0 \\ β \end{array}], 𝑨 = [\begin{array}{ll} T (𝒆_{1}) & T (𝒆_{2}) \end{array}] = [\begin{array}{ll} α & 0 \\ 0 & β \end{array}]$ $T ([\begin{array}{l} 2 \\ 1 \end{array}]) = [\begin{array}{l} 2 α \\ β \end{array}] = [\begin{array}{ll} α & 0 \\ 0 & β \end{array}] [\begin{array}{l} 2 \\ 1 \end{array}]$
In general a diagonal matrix describes stretching with factors $λ_{1}, λ_{2}, \dots, λ_{m} > 0$
$𝑨 = [\begin{array}{llll} λ_{1} & 0 & \dots & 0 \\ 0 & λ_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & λ_{m} \end{array}]$

Orthogonal projection

Orthogonal projection of $𝒗 \in ℝ^{m}$ along direction $𝒖 \in ℝ^{m}$ , $|| 𝒖 || = 1$

Figure 1. Orthogonal projection operation $P_{𝒖}$ .

$𝒘 = (|| 𝒗 || \cos θ) 𝒖 = (|| 𝒗 ||) 𝒖 = (𝒖^{T} 𝒗) 𝒖 = 𝒖 (𝒖^{T} 𝒗) = (𝒖 𝒖^{T}) 𝒗 \Rightarrow$
Projection matrix $𝑷_{𝒖} = 𝒖 𝒖^{T}$ ( $|| 𝒖 || = 1$ )

Orthogonal projection examples

Projection along $𝒆_{1}$ direction in $ℝ^{2}$
$𝑷_{𝒆_{1}} = [\begin{array}{l} 1 \\ 0 \end{array}] [1 \begin{array}{ll} 0 \end{array}] = [\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}], 𝑷_{𝒆_{1}} [\begin{array}{l} x_{1} \\ x_{2} \end{array}] = [\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] = [\begin{array}{l} x_{1} \\ 0 \end{array}] .$
Projection along direction of vector $𝒘 = [\begin{array}{l} 1 \\ 1 \\ 1 \end{array}]$ in $ℝ^{3}$ :
- First obtain a vector of unit norm $𝒖 = 𝒘 / || 𝒘 || = \frac{1}{\sqrt{3}}$ $[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}]$
- Projection matrix
  $𝑷_{𝒖} = 𝒖 𝒖^{T} = \frac{1}{3} [\begin{array}{l} 1 \\ 1 \\ 1 \end{array}] [\begin{array}{lll} 1 & 1 & 1 \end{array}] = \frac{1}{3} [\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}] .$

Reflection

Reflection of $𝒖 \in ℝ^{2}$ across $x_{1}$ axis
$T (𝒆_{1}) = [\begin{array}{l} 1 \\ 0 \end{array}], T (𝒆_{2}) = [\begin{array}{l} 0 \\ - 1 \end{array}], 𝑨 = [\begin{array}{ll} 1 & 0 \\ 0 & - 1 \end{array}], 𝑨 [\begin{array}{l} x_{1} \\ x_{2} \end{array}] = [\begin{array}{l} x_{1} \\ - x_{2} \end{array}] .$

Reflection of $𝒖 \in ℝ^{2}$ across $𝒘 \in ℝ^{2}$ , $|| 𝒘 || = 1$ , $𝒗 = T_{𝒘} (𝒖) = 𝑨 𝒖$ . Two steps:

Project $𝒖$ onto direction of $𝒘$ , $𝒚 = 𝒘 𝒘^{T} 𝒖$ , $𝒚 = 𝒖 + 𝒛$ .
Go from $𝒖$ twice the vector $𝒛$ to obtain the reflection
$𝒗 = 𝑨 𝒖 = 𝒖 + 2 𝒛 = 𝒖 + 2 (𝒚 - 𝒖) = - 𝒖 + 2 𝒘 𝒘^{T} 𝒖 = (2 𝒘 𝒘^{T} - 𝑰) 𝒖$

Figure 2. Reflection matrix diagram $𝑨 = 2 𝒘 𝒘^{T} - 𝑰$ .

Reflection example

Reflect $𝒆_{2}$ across $𝒘 = \frac{1}{\sqrt{2}} [\begin{array}{l} 1 \\ 1 \end{array}] .$
$𝑨 = 2 𝒘 𝒘^{T} - 𝑰 = [\begin{array}{l} 1 \\ 1 \end{array}] [\begin{array}{ll} 1 & 1 \end{array}] - [\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}] = [\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}]$ $𝑨 𝒆_{2} = [\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}] [\begin{array}{l} 0 \\ 1 \end{array}]$

Rotation in

ℝ^{2}

Construct standard rotation matrix by rotating $𝒆_{1}, 𝒆_{2}$

𝑨 = [\begin{array}{ll} T (𝒆_{1}) & T (𝒆_{2}) \end{array}] = [\begin{array}{ll} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array}]

Figure 3. Diagram for construction of rotation matrix

Transformation composition

Consider two transformations $S (𝒖) = 𝑨 𝒖$ , $T (𝒖) = 𝑩 𝒖$ . Composition $S (T (𝒖))$
$R (𝒖) = S (T (𝒖)) = S (𝑩 𝒖) = 𝑨 𝑩 𝒖 = 𝑪 𝒖$
Matrix of transformation composition is product of the individual transformation matrices
Example: Rotation by $φ$ followed by rotation by $θ$ in $ℝ^{2}$
$[\begin{array}{ll} \cos (θ + φ) & - \sin (θ + φ) \\ \sin (θ + φ) & \cos (θ + φ) \end{array}] = [\begin{array}{ll} \cos (θ) & - \sin (θ) \\ \sin (θ) & \cos (θ) \end{array}] [\begin{array}{ll} \cos (φ) & - \sin (φ) \\ \sin (φ) & \cos (φ) \end{array}]$ $\cos (θ + φ) = \cos (θ) \cos (φ) - \sin (θ) \sin (φ)$ $\sin (θ + φ) = \sin (θ) \cos (φ) + \cos (θ) \sin (φ)$