MATH347

MATH347 L12: Fundamental Theorem of Linear Algebra

New concepts:
- Vector space sums
- FTLA
- FTLA step-by-step (question by question) proof
- Rank-nullity theorem
- Characterizing solutions to linear systems in terms of rank and nullity

Direct sum, intersection of vector spaces

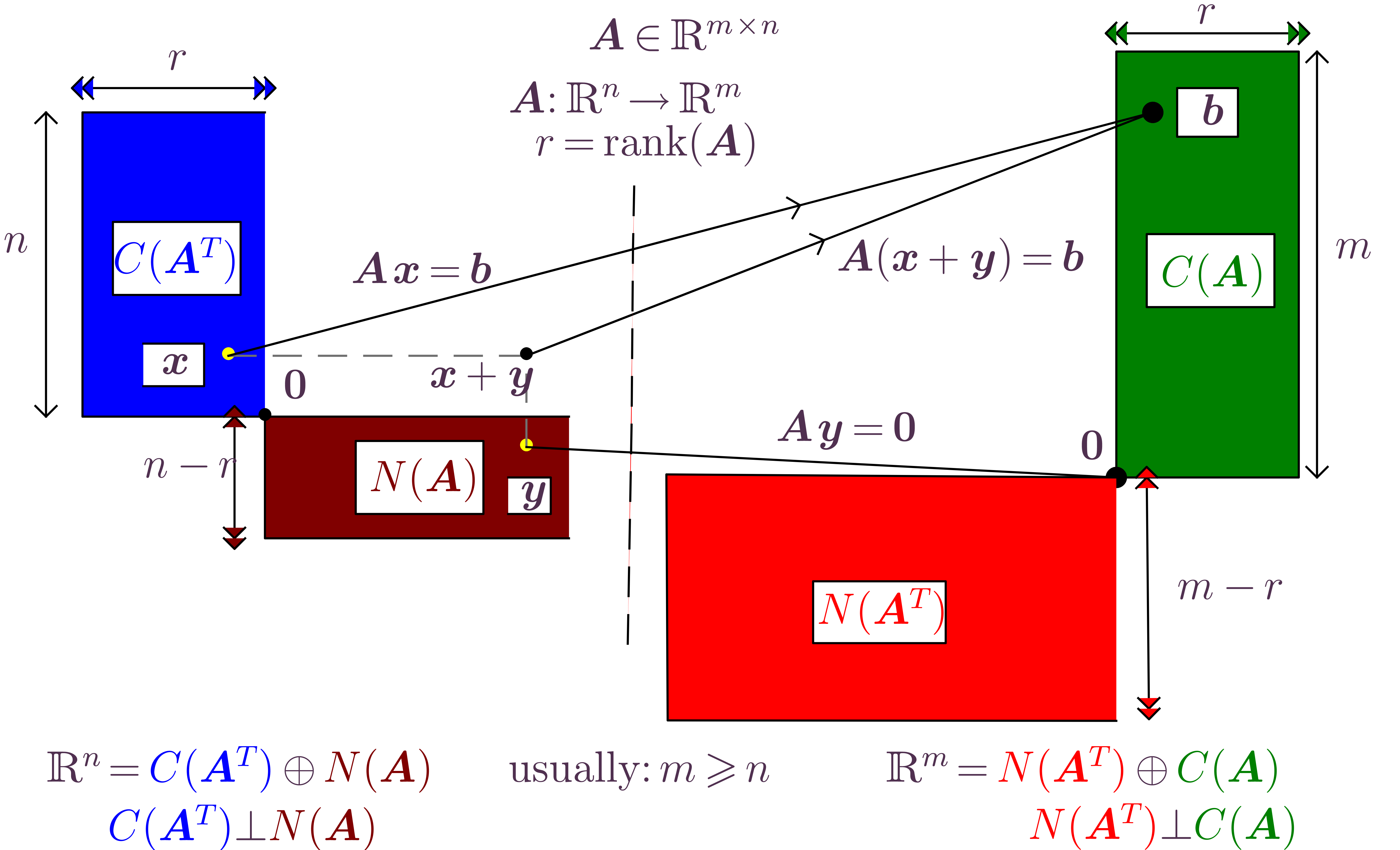
Definition. Given two vector subspaces $(𝒰, 𝒮, +)$ , $(𝒱, 𝒮, +)$ of the space $(𝒲, 𝒮, +)$ , the sum is the set $𝒰 + 𝒱 = {𝒖 + 𝒗 | 𝒖 \in 𝒰, 𝒗 \in 𝒱} .$

Definition. Given two vector subspaces $(𝒰, 𝒮, +)$ , $(𝒱, 𝒮, +)$ of the space $(𝒲, 𝒮, +)$ , the direct sum is the set $𝒰 \oplus 𝒱 = {𝒖 + 𝒗 | \exists! 𝒖 \in 𝒰, \exists! 𝒗 \in 𝒱} .$ (unique decomposition)

Definition. Given two vector subspaces $(𝒰, 𝒮, +)$ , $(𝒱, 𝒮, +)$ of the space $(𝒲, 𝒮, +)$ , the intersection is the set

$𝒰 \cap 𝒱 = {𝒙 | 𝒙 \in 𝒰, 𝒙 \in 𝒱} .$

Definition. Two vector subspaces $(𝒰, 𝒮, +)$ , $(𝒱, 𝒮, +)$ of the space $(𝒲, 𝒮, +)$ are orthogonal subspaces, denoted $𝒰 ⊥ 𝒱$ if $𝒖^{T} 𝒗 = 0$ for any $𝒖 \in 𝒰, 𝒗 \in 𝒱$ .

Definition. Two vector subspaces $(𝒰, 𝒮, +)$ , $(𝒱, 𝒮, +)$ of the space $(𝒲, 𝒮, +)$ are orthogonal complements, denoted $𝒰 = 𝒱^{⊥}$ , $𝒱 = 𝒰^{⊥}$ if they are orthogonal subspaces and $𝒰 \cap 𝒱 = {𝟎}$ , i.e., the null vector is the only common element of both subspaces.

Recapitulation: The four fundamental subspaces for a linear mapping

A matrix $𝑨 \in ℝ^{m \times n}$ is a linear mapping from $ℝ^{n}$ to $ℝ^{m}$ , $𝑨 : ℝ^{n} \to ℝ^{m}$
The transpose $𝑨^{T} \in ℝ^{n \times m}$ is a linear mapping from $ℝ^{m}$ to $ℝ^{n}$ , $𝑨^{T} : ℝ^{m} \to ℝ^{n}$
To each matrix $𝑨 \in ℝ^{m \times n}$ associate four fundamental subspaces:
1. Column space, $C (𝑨) = {𝒃 \in ℝ^{m} | \exists 𝒙 \in ℝ^{n} such that 𝒃 = 𝑨 𝒙} \subseteq ℝ^{m}$ , the part of $ℝ^{m}$ reachable by linear combination of columns of $𝑨$
2. Left null space, $N (𝑨^{T}) = {𝒚 \in ℝ^{m} | 𝑨^{T} 𝒚 = 0} \subseteq ℝ^{m}$ , the part of $ℝ^{m}$ not reachable by linear combination of columns of $𝑨$
3. Row space, $R (𝑨) = C (𝑨^{T}) = {𝒄 \in ℝ^{n} | \exists 𝒚 \in ℝ^{m} such that 𝒄 = 𝑨^{T} 𝒚} \subseteq ℝ^{n}$ , the part of $ℝ^{n}$ reachable by linear combination of rows of $𝑨$
4. Null space, $N (𝑨) = {𝒙 \in ℝ^{n} | 𝑨 𝒙 = 0} \subseteq ℝ^{n}$ , the part of $ℝ^{n}$ not reachable by linear combination of rows of $𝑨$

FTLA

Theorem. Given the linear mapping associated with matrix $𝑨 \in ℝ^{m \times n}$ we have:

$C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ , the direct sum of the column space and left null space is the codomain of the mapping

$C (𝑨^{T}) \oplus N (𝑨) = ℝ^{n}$ , the direct sum of the row space and null space is the domain of the mapping

$C (𝑨) ⊥ N (𝑨^{T})$ and $C (𝑨) \cap N (𝑨^{T}) = {𝟎}$ , the column space is orthogonal to the left null space, and they are orthogonal complements of one another,
$\begin{array}{ll} C (𝑨) = N {(𝑨^{T})}^{⊥}, & N (𝑨^{T}) = C {(𝑨)}^{⊥} \end{array} .$

$C (𝑨^{T}) ⊥ N (𝑨)$ and $C (𝑨^{T}) \cap N (𝑨) = {𝟎}$ , the row space is orthogonal to the null space, and they are orthogonal complements of one another,
$\begin{array}{ll} C (𝑨^{T}) = N {(𝑨)}^{⊥}, & N (𝑨) = C {(𝑨^{T})}^{⊥} \end{array} .$

Graphical representation of FTLA

Proofs

Understanding the FTLA is essential to applications
Proofs of the FTLA help in:
- building the ability to recognize rigorous mathematical arguments as opposed to intuition
- gaining an appreciation of the interplay between construction of mathematical concepts (formalized in a definition) and interaction between these concepts (propositions and theorems).
Recall: linear algebra seeks construction of complex objects, vectors $𝒃 \in ℝ^{m}$ through linear combination of $n$ column vectors organized into a matrix

$𝑨 = [\begin{array}{lll} 𝒂_{1} & \dots & 𝒂_{n} \end{array}]$ , $𝒃 = T (𝒙) = 𝑨 𝒙$ , $𝑨 \in ℝ^{m \times n}$ , $𝒙 \in ℝ^{n}$ scaling coefficients.

$T : ℝ^{n} \to ℝ^{m}$ a linear mapping from domain $ℝ^{n}$ to codomain $ℝ^{m}$ .

A proof of the FTLA is now presented as answers (first informal, and then rigorous) to a series of natural questions arising from the initial goal:
1. What vectors can be obtained by the linear combination $𝑨 𝒙$ ?
2. Is there only one way to obtain a vector $𝒃$ by linear combination?
3. Is there a preferred way to describe vectors $𝒃 = 𝑨 𝒙$ ?
4. Is there a preferred way to describe vectors $𝒚$ that satisfy $𝑨 𝒚 = 𝟎$ ?
5. Is there anything different about organizing vectors into rows?

Q1: What vectors can be obtained by the linear combination

𝑨 𝒙

?

Set of reachable vectors: defined by column space of $𝑨$ (range of mapping $T$ )
$C (𝑨) = {𝒃 | \exists 𝒙 \in ℝ^{n}, 𝒃 = 𝑨 𝒙 .} \subseteq ℝ^{m}$
$C (𝑨)$ has structure, it is a vector subspace of $ℝ^{m}$ , $C (𝑨) \leq ℝ^{m}$

Proof. $\forall 𝒖, 𝒗 \in C (𝑨) \Rightarrow \exists 𝒙, 𝒚 \in ℝ^{n}$ such that $𝒖 = 𝑨 𝒙, 𝒗 = 𝑨 𝒚$ by definition of $C (𝑨)$ . Then $𝒖 + 𝒗 = 𝑨 𝒙 + 𝑨 𝒚 = 𝑨 (𝒙 + 𝒚)$ , hence $𝒖 + 𝒗 \in C (𝑨)$ .
”Size” of a vector space has been characterized by the concept of dimension. Give a distinct name to the “size” of the set of reachable vectors.

Definition. The rank of a matrix $𝑨 \in ℝ^{m \times n}$ is the dimension of the column space

$r = \dim C (𝑨)$

Q2: Is there only one way to obtain a vector

𝒃

by linear combination?

Suppose $𝒃 = 𝑨 𝒙$ , could $𝒃$ also be obtained differently, as $𝒃 = 𝑨 (𝒙 + 𝒚)$ ?
Subtracting the two linear combinations leads to $𝑨 𝒚 = 𝟎$ , and the null space
$N (𝑨) = {𝒚 | 𝑨 𝒚 = 𝟎 .} \subseteq ℝ^{n} .$
$N (𝑨)$ has structure, it is a vector subspace of $ℝ^{n}$ , $N (𝑨) \leq ℝ^{n}$

Proof. $\forall 𝒖, 𝒗 \in N (𝑨) \Rightarrow 𝑨 𝒖 = 𝟎, 𝑨 𝒗 = 𝟎 \Rightarrow 𝑨 (𝒖 + 𝒗) = 𝟎 \Rightarrow$ $𝒖 + 𝒗 \in N (𝑨)$ .
Obviously, $𝟎 \in N (𝑨)$ , but the null space might also contain non-zero vectors
Even when $𝑨 \neq 𝟎$ (i.e., $𝑨$ is not the zero matrix) and $𝒚 \neq 𝟎$ (i.e., $𝒚$ is not the zero vector), there still might be choices of $𝑨$ and $𝒚$ such that $𝑨 𝒚 = 𝟎$ . This is different from $a, x \in ℝ$ , where $a x = 0 \Rightarrow a = 0 or x = 0$ .
Give a distinct name to the “size” of the set of such vectors.

Definition. The nullity of a matrix $𝑨 \in ℝ^{m \times n}$ is the dimension of the null space

$z = \dim N (𝑨)$

Q3: Is there a preferred way to describe vectors

𝒃 = 𝑨 𝒙

?

Since $r = \dim C (𝑨)$ and $C (𝑨)$ is a vector subspace of $ℝ^{m}$ , $r ⩽ m$ .
The above implies that only $r$ of the $n$ columns of $𝑨$ are linearly independent
Gather the linearly independent columns as the first $r$ columns
$𝑨 = [\begin{array}{ll} 𝑨_{r} & 𝑨_{n - r} \end{array}], 𝑨_{r} \in ℝ^{m \times r}, 𝑨_{n - r} \in ℝ^{m \times (n - r)},$
a block decomposition of $𝑨$ , with the index denoting number of columns.
Since columns $𝑨_{n - r}$ are linearly dependent on those of $𝑨_{r}$ , $𝑨_{n - r} = 𝑨_{r} 𝑩_{n - r}$
$𝑨 = 𝑨_{r} [\begin{array}{ll} 𝑰_{r} & 𝑩_{n - r} \end{array}] = 𝑨_{r} 𝑿, 𝑿 \in ℝ^{r \times n}$
The above states: “all the column vectors of $𝑨$ can be expressed as linear combinations of $r$ linearly independent columns, $𝑨_{r}$ .

Q4:Is there a preferred way to describe vectors

𝒚

that satisfy

𝑨 𝒚 = 𝟎

?

Consider now $N (𝑨)$ : $𝑨 𝒖 = 𝑨_{r} 𝑿 𝒖 = 𝟎$
Let $𝒗 = 𝑿 𝒖$ . $𝑨_{r}$ with linearly independent columns, $𝑨_{r} 𝒗 = 𝟎 \Rightarrow 𝒗 = 0 \Rightarrow 𝑿 𝒖 = 𝟎$ . Write this out in blocks
$[\begin{array}{ll} 𝑰_{r} & 𝑩_{n - r} \end{array}] [\begin{array}{l} 𝒖_{r} \\ 𝒖_{n - r} \end{array}] = 𝟎 \Rightarrow 𝒖 = [\begin{array}{l} - 𝑩_{n - r} \\ 𝑰_{n - r} \end{array}] 𝒖_{n - r} = 𝒀_{n - r} 𝒖_{n - r} .$

This states that columns of $𝒀_{n - r}$ are a spanning set for $N (𝑨)$ , $𝒖 = 𝒀_{n - r} 𝒖_{n - r} .$
Is it a minimal spanning set, i.e., a basis? Consider
$𝒀_{n - r} 𝒘 = 𝟎 \Rightarrow [\begin{array}{l} - 𝑩_{n - r} \\ 𝑰_{n - r} \end{array}] 𝒘 = [\begin{array}{l} - 𝑩_{n - r} 𝒘 \\ 𝒘 \end{array}] = [\begin{array}{l} 𝟎 \\ 𝟎 \end{array}] \Rightarrow 𝒘 = 𝟎 .$
Indeed columns of $𝒀_{n - r}$ are linearly independent, establishing that
$z = \dim N (𝑨) = n - r$

Theorem. (Rank-nullity theorem) For $𝑨 \in ℝ^{m \times n}$ , $r + z = n$

Q5: Is there anything different about organizing vectors into rows?

Matrix vector multiplication $𝒃 = 𝑨 𝒙 = x_{1} 𝒂_{1} + \dots + x_{n} 𝒂_{n},$ expresses a linear combination of columns. Multiple linear combination of columns: $𝑩 = 𝑨 𝑿$ .
Organizing data into column vectors is an arbitrary choice, hence linear combinations of rows should also be possible, and indeed are expressed as
$𝒄^{T} = 𝒚^{T} 𝑨 \Rightarrow 𝒄 = 𝑨^{T} 𝒚 .$
$𝒄^{T}$ : the row vector obtained by linear combination of rows of $𝑨$ with scaling coefficients gathered in the row vector $𝒚^{T}$ . Multiple linear combinations of rows
$𝑪 = 𝒀 𝑨$
Rows of $𝑪$ are linear combination of rows of $𝑨$ with scalings as rows of $𝒀$ .
The set of vectors reachable by linear combination of rows of $𝑨$ is $C (𝑨^{T})$
$C (𝑨^{T}) = {𝒄 | \exists 𝒚 \in ℝ^{m}, 𝒄 = 𝑨^{T} 𝒚 .} \leq ℝ^{n},$
the row space or column space of the transpose, and is a subspace of $ℝ^{n}$ .
Let $p = \dim C (𝑨^{T})$ , the dimension of the row space.

Dimensions of row, column spaces are equal

Proposition. The dimension of the column space equals that of the row space

$r = \dim C (𝑨) = \dim C (𝑨^{T}) = p .$

Proof. Interpret $𝑨 = 𝑨_{r} 𝑿$ as stating that the rows of $𝑨$ can be obtained linear combinations of the rows of $𝑿$ with scalings contained in $𝑨_{r}$ . Since $𝑿 \in ℝ^{r \times n}$ ,

p = \dim C (𝑨^{T}) ⩽ r = \dim C (𝑨) .

The above is true for any matrix $𝑴$ , $\dim C (𝑴^{T}) ⩽ \dim C (𝑴) .$ Choose $𝑴 = 𝑨^{T}$

\dim C ({(𝑨^{T})}^{T}) ⩽ \dim C (𝑨^{T}) \Rightarrow r = \dim C (𝑨) ⩽ \dim C (𝑨^{T}) = p .

Since $p ⩽ r$ and $r ⩽ p$ , it results that $r = p .$

FTLA components

Results up to now can be used to prove:

$C (𝑨)$ is orthogonal to $N (𝑨^{T})$ .

Proof. $𝒖 \in C (𝑨) \Rightarrow 𝒖 = 𝑨 𝒙$ , $𝒗 \in N (𝑨^{T}) \Rightarrow 𝑨^{T} 𝒗 = 𝟎$ . Compute $𝒖^{T} 𝒗 = 𝒙^{T} 𝑨^{T} 𝒗 = 𝒙^{T} 𝟎 = 𝟎 .$
$𝟎$ is the only vector both in $C (𝑨)$ and $N (𝑨^{T})$ .

Proof. Assume there might be $𝒃 \in C (𝑨)$ and $b \in N (𝑨^{T})$ and $𝒃 \neq 𝟎$ . Since $𝒃 \in C (𝑨)$ , $\exists 𝒙 \in ℝ^{n}$ such that $𝒃 = 𝑨 𝒙$ . Since $𝒃 \in N (𝑨^{T})$ , $𝑨^{T} 𝒃 = 𝑨^{T} (𝑨 𝒙) = 𝟎$ . Note that $𝒙 \neq 0$ since $𝒙 = 0 \Rightarrow 𝒃 = 0$ , contradicting assumptions. Multiply equality $𝑨^{T} 𝑨 𝒙 = 𝟎$ on left by $𝒙^{T}$ ,
$𝒙^{T} 𝑨^{T} 𝑨 𝒙 = 𝟎 \Rightarrow {(𝑨 𝒙)}^{T} (𝑨 𝒙) = 𝒃^{T} 𝒃 = {|| 𝒃 ||}^{2} = 0 \Rightarrow 𝒃 = 0 .$
$C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ . Rank-nullity theorem states $\dim C (𝑨) + \dim N (𝑨^{T}) = m$ , thereby covering the entire codomain, $ℝ^{m}$ .