MATH347

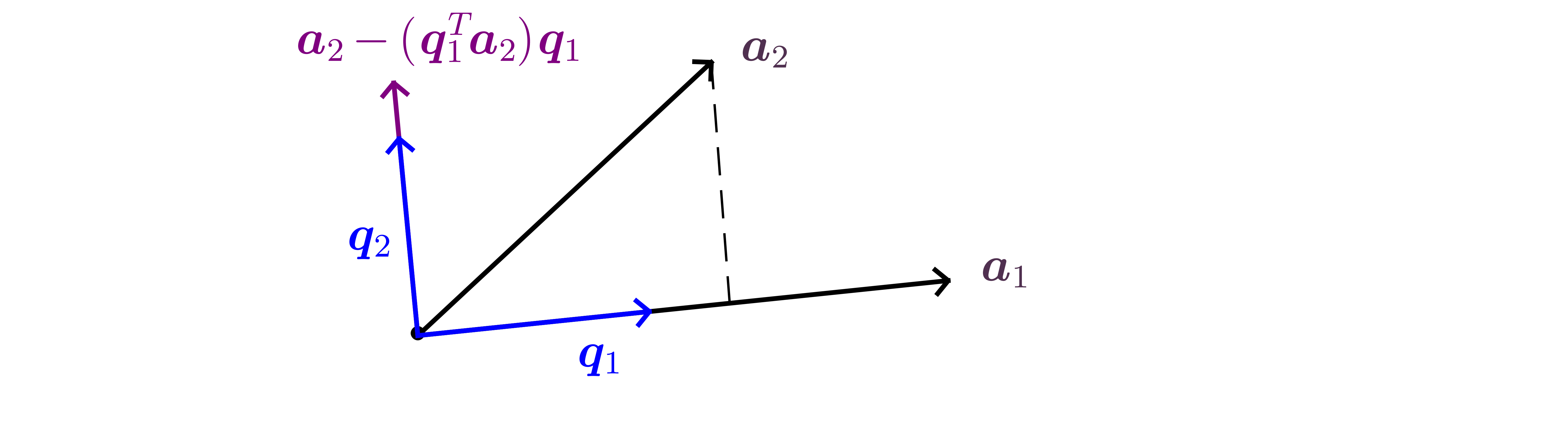
MATH347 L13: Orthonormal bases

New concepts:
- Orthonormal vector set
- Transforming a basis set into an orthonormal set by Gram-Schmidt
- $𝑸 𝑹$ factorization of a matrix
- Orthonormal bases for column, null space

Orthonormal vector set

Definition. The Dirac delta symbol $δ_{i j}$ is defined as

$δ_{i j} = {\begin{cases} 1 & if i = j \\ 0 & if i \neq j \end{cases}$

Definition. A set of vectors ${𝒖_{1}, \dots, 𝒖_{n}}$ is said to be orthonormal if

$𝒖_{i}^{T} 𝒖_{j} = δ_{i j}$

The column vectors of the identity matrix are orthonormal
$𝑰 = (\begin{array}{ccc} 𝒆_{1} & \dots & 𝒆_{m} \end{array}), 𝒆_{i}^{T} 𝒆_{j} = δ_{i j}, 𝑰^{T} 𝑰 = 𝑰$
Columns of $𝑸 = [\begin{array}{lll} 𝒒_{1} & \dots & 𝒒_{n} \end{array}] \in ℝ^{m \times n}$ are orthonormal if
$𝑸^{T} 𝑸 = [\begin{array}{l} 𝒒_{1}^{T} \\ ⋮ \\ 𝒒_{n}^{T} \end{array}] [\begin{array}{lll} 𝒒_{1} & \dots & 𝒒_{n} \end{array}] = [\begin{array}{llll} 𝒒_{1}^{T} 𝒒_{1} & 𝒒_{1}^{T} 𝒒_{2} & \dots & 𝒒_{1}^{T} 𝒒_{n} \\ 𝒒_{2}^{T} 𝒒_{1} & 𝒒_{2}^{T} 𝒒_{2} & \dots & 𝒒_{2}^{T} 𝒒_{n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 𝒒_{n}^{T} 𝒒_{1} & 𝒒_{n}^{T} 𝒒_{2} & \dots & 𝒒_{n}^{T} 𝒒_{n} \end{array}] = 𝑰_{n}$

Gram-Schmidt procedure idea

Transform columns of $𝑨 = [\begin{array}{lll} 𝒂_{1} & \dots & 𝒂_{n} \end{array}]$ into $𝑸 = [\begin{array}{lll} 𝒒_{1} & \dots & 𝒒_{n} \end{array}]$ , $𝑸^{T} 𝑸 = 𝑰_{n}$
Idea:
- Start with an arbitrary direction $𝒂_{1}$
- Divide by its norm to obtain a unit-norm vector $𝒒_{1} = 𝒂_{1} / || 𝒂_{1} ||$
- Choose another direction $𝒂_{2}$
- Subtract off its component along previous direction(s) $𝒂_{2} - (𝒒_{1}^{T} 𝒂_{2}) 𝒒_{1}$
- Divide by norm $𝒒_{2} = (𝒂_{2} - (𝒒_{1}^{T} 𝒂_{2}) 𝒒_{1}) / || 𝒂_{2} - (𝒒_{1}^{T} 𝒂_{2}) 𝒒_{1} ||$
- Repeat the above

Gram-Schmidt algebra

Observe that formulas such as
$𝒒_{2} = (𝒂_{2} - (𝒒_{1}^{T} 𝒂_{2}) 𝒒_{1}) / || 𝒂_{2} - (𝒒_{1}^{T} 𝒂_{2}) 𝒒_{1} ||$
state: “ $𝒒_{2}$ is obtained as a linear combination of $𝒂_{2}$ and $𝒒_{1}$ ”
Use column structure of $𝑨, 𝑸$
$𝑨 = [\begin{array}{llll} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}] = [\begin{array}{llll} 𝒒_{1} & 𝒒_{2} & \dots & 𝒒_{n} \end{array}] [\begin{array}{llll} r_{11} & r_{12} & \dots & r_{1 n} \\ 0 & r_{22} & \dots & r_{2 n} \\ ⋮ & ⋱ \\ 0 & 0 & \dots & r_{n n} \end{array}] = 𝑸 𝑹$
Identify on both sides to obtain
$\begin{array}{l} 𝒂_{1} = r_{11} 𝒒_{1} \\ 𝒂_{2} = r_{12} 𝒒_{1} + r_{2 2} 𝒒_{2} \\ 𝒂_{3} = r_{13} 𝒒_{1} + r_{23} 𝒒_{2} + r_{3 3} 𝒒_{3} \\ ⋮ \\ 𝒂_{n} = r_{1 n} 𝒒_{1} + r_{2 n} 𝒒_{2} + r_{3 n} 𝒒_{3} + \dots + r_{n n} 𝒒_{n} \end{array} \begin{array}{l} 𝒒_{1} = 𝒂_{1} / r_{11} \\ 𝒒_{2} = (𝒂_{2} - r_{12} 𝒒_{1}) / r_{2 2} \\ 𝒒_{3} = (𝒂_{3} - r_{13} 𝒒_{1} - r_{23} 𝒒_{2}) / r_{3 3} \\ ⋮ \end{array}$

Gram-Schmidt algorithm

Algorithm (Gram-Schmidt)

Given $n$ vectors $𝒂_{1}, \dots, 𝒂_{n}$

Initialize $𝒒_{1} = 𝒂_{1}$ ,.., $𝒒_{n} = 𝒂_{n}$ , $𝑹 = 𝑰_{n}$

for $i = 1$ to $n$

$r_{i i} = {(𝒒_{i}^{T} 𝒒_{i})}^{1 / 2}$ ; $𝒒_{i} = 𝒒_{i} / r_{i i}$

for $j = i$ +1 to $n$

$r_{i j} = 𝒒_{i}^{T} 𝒂_{j}$ ; $𝒒_{j} = 𝒒_{j} - r_{i j} 𝒒_{i}$

end

return $𝑸, 𝑹$

Orthonormal bases for fundamental matrix spaces

Matlab orth returns basis for $C (𝑨)$
>>

A=[1 -2 1 -1; 1 1 1 -1; 1 0 1 -1]; orth(A)
$(\begin{array}{cc} 0.7475 & - 0.6081 \\ 0.4101 & 0.7390 \\ 0.5226 & 0.2900 \end{array})$
Matlab null returns basis for $N (𝑨)$
>>

A=[1 -2 1 -1; 1 1 1 -1; 1 0 1 -1]; orth(A)
$(\begin{array}{cc} 0.7475 & - 0.6081 \\ 0.4101 & 0.7390 \\ 0.5226 & 0.2900 \end{array})$
>>

rref(A)
$(\begin{array}{cccc} 1 & 0.0 & 1 & - 1 \\ 0.0 & 1 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 \end{array})$
>>