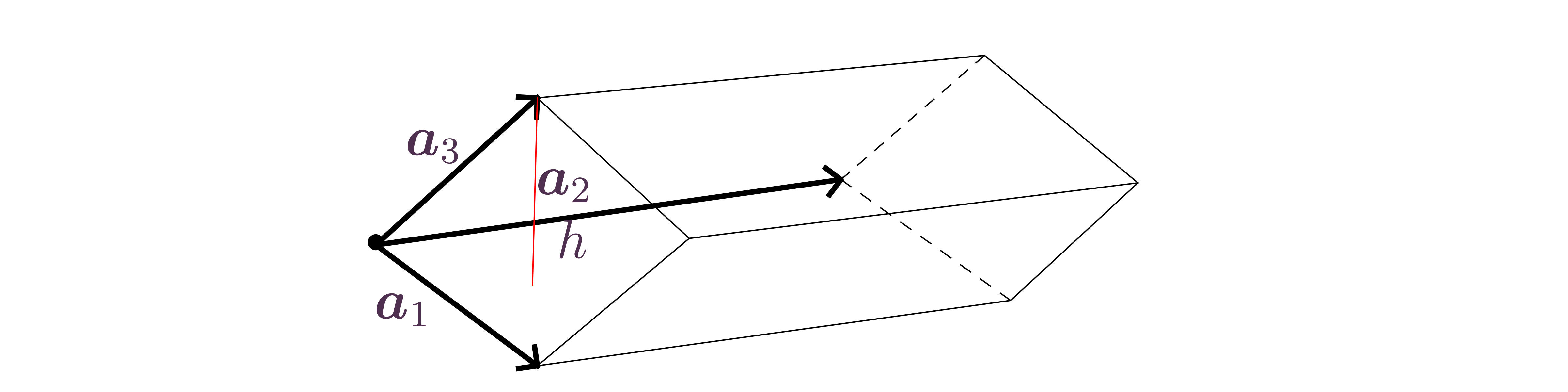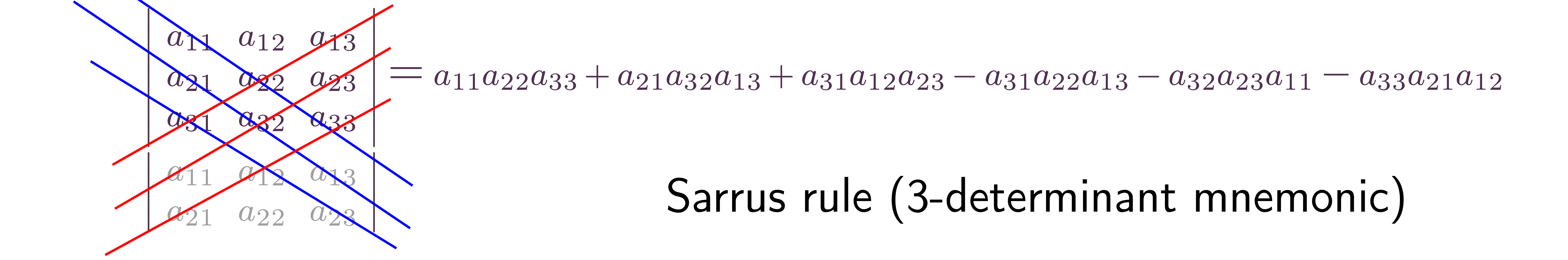MATH347

MATH347 L17: Determinants

New concepts:
- Geometric definition: volume of a hyper-parallelipiped
- Determinant calculation rules
- Algebraic definition: sum over permutations
- Example of a bad algorithm: Cramer's rule

Geometric definition

Definition. The determinant of a square matrix $𝑨 = [\begin{array}{lll} 𝒂_{1} & \dots & 𝒂_{m} \end{array}] \in ℝ^{m \times m}$

$\det (A) = | \begin{array}{cccc} a_{11} & a_{12} & \dots & a_{1 m} \\ a_{21} & a_{22} & \dots & a_{2 m} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m 1} & a_{m 2} & \dots & a_{m m} \end{array} | \in ℝ$

is a real number giving the (oriented) volume of the parallelepiped spanned by matrix column vectors.

$m = 2$
$𝑨 = [\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}],, \det (𝑨) = | \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} | .$
$m = 3$
$𝑨 = [\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}],, \det (𝑨) = | \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} | .$

Determinants of

m = 2

,

m = 3

size matrices

Computation of a determinant with $m = 2$
$| \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} | = a_{11} a_{22} - a_{12} a_{21}$
Computation of a determinant with $m = 3$
$\begin{array}{rcl} | \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} | & = & a_{11} a_{22} a_{33} + a_{21} a_{32} a_{13} + a_{31} a_{12} a_{23} \\ - a_{13} a_{22} a_{31} - a_{23} a_{32} a_{11} - a_{33} a_{12} a_{21} \end{array}$
Where do these determinant computation rules come from? Three viewpoints
- Geometry viewpoint: determinants express parallelepiped volumes
- Algebra viewpoint: determinants are computed from all possible products that can be formed from choosing a factor from each row and each column
- Function viewpoint: the determinant is a function satisfying certain properties (see Textbook Definition 3.2.1).

Determinant in 2D gives area of parallelogram

$m = 2$
In two dimensions a “parallelepiped” becomes a parallelogram with area given as
$(Area) = (Length of Base) \times (Length of Height)$
Take $𝒂_{1}$ as the base, with length $b = || 𝒂_{1} ||$ . Vector $𝒂_{1}$ is at angle $φ_{1}$ to $x_{1}$ -axis, $𝒂_{2}$ is at angle $φ_{2}$ to $x_{2}$ -axis, and the angle between $𝒂_{1}$ , $𝒂_{2}$ is $θ = φ_{2} - φ_{1}$ . The height has length
$h = || 𝒂_{2} || \sin θ = || 𝒂_{2} || \sin . (. φ_{2} - φ_{1}) = || 𝒂_{2} || (\sin φ_{2} \cos φ_{1} - \sin φ_{1} \cos φ_{2})$
Use $\cos φ_{1} = a_{11} / || 𝒂_{1} ||$ , $\sin φ_{1} = a_{12} / || 𝒂_{1} ||$ , $\cos φ_{2} = a_{21} / || 𝒂_{2} ||$ , $\sin φ_{2} = a_{22} / || 𝒂_{2} ||$
$(Area) = || 𝒂_{1} || || 𝒂_{2} || (\sin φ_{2} \cos φ_{1} - \sin φ_{1} \cos φ_{2}) = a_{11} a_{22} - a_{12} a_{21}$

Determinant in 3D gives volume of parallelepiped

$m = 3$ , $𝑨 = [\begin{array}{lll} 𝒂_{1} & 𝒂_{2} & 𝒂_{3} \end{array}]$

The volume is (area of base) $\times$ (height) and given as the value of the determinant

\det (𝑨) = | \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} |

Determinants measure mapping deformation of unit hypercube

Recall that $𝑨 = [\begin{array}{lll} 𝒂_{1} & \dots & 𝒂_{m} \end{array}] \in ℝ^{m \times m}$ defines a linear mapping $T (𝒙) = 𝑨 𝒙$
Observe
$T (𝒆_{1}) = 𝑨 𝒆_{1} = 𝒂_{1}, \dots, T (𝒆_{m}) = 𝑨 𝒆_{m} = 𝒂_{m}$
Since $T : ℝ^{m} \to ℝ^{m}$ , interpret above to mean that $\det (𝑨)$ measures the ratio of the volume of the hyperparallelipiped $[\begin{array}{lll} 𝒂_{1} & \dots & 𝒂_{m} \end{array}]$ w.r.t. unit hypercube

From above, observe that the determinant can be used to “measure” both a matrix and a linear mapping.

Determinant calculations

The geometric interpretation of a determinant as an oriented volume is useful in establishing rules for calculation with determinants:
- Determinant of matrix with repeated columns is zero (since two edges of the parallelepiped are identical). Example for $m = 3$
  $Δ = | \begin{array}{ccc} a & a & u \\ b & b & v \\ c & c & w \end{array} | = a b w + b c u + c a v - u b c - v c a - w a b = 0$
  This is more easily seen using the column notation
  $Δ = \det [\begin{array}{llll} 𝒂_{1} & 𝒂_{1} & 𝒂_{3} & \dots \end{array}] = 0$
- Determinant of matrix with linearly dependent columns is zero (since one edge lies in the 'hyperplane' formed by all the others)

Determinant calculation rules

Separating sums in a column (similar for rows). With $𝒂_{i}, 𝒃_{1} \in ℝ^{m}$ :
$\det [\begin{array}{llll} 𝒂_{1} + 𝒃_{1} & 𝒂_{2} & \dots & 𝒂_{m} \end{array}] = \det [\begin{array}{llll} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{m} \end{array}] + \det [\begin{array}{llll} 𝒃_{1} & 𝒂_{2} & \dots & 𝒂_{m} \end{array}]$
Scalar product in a column (similar for rows). With $α \in ℝ$ :
$\det [\begin{array}{llll} α 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{m} \end{array}] = α \det \begin{array}{llll} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{m} \end{array}$
Linear combinations of columns (similar for rows). With $α \in ℝ$ :
$\det [\begin{array}{llll} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{m} \end{array}] = \det [\begin{array}{llll} 𝒂_{1} & α 𝒂_{1} + 𝒂_{2} & \dots & 𝒂_{m} \end{array}]$
Swapping two columns (or rows) changes determinant sign
$\det [\begin{array}{lllllll} 𝒂_{1} & \dots & 𝒂_{i} & \dots & 𝒂_{j} & \dots & 𝒂_{m} \end{array}] = - \det [\begin{array}{lllllll} 𝒂_{1} & \dots & 𝒂_{j} & \dots & 𝒂_{i} & \dots & 𝒂_{m} \end{array}]$

Minors and cofactors

For $𝑨 \in ℝ^{m \times m}$ , the $(i, j)$ -minor of $𝑨$ , $m_{i, j}$ , is the $(m - 1) \times (m - 1)$ determinant obtained by deleting row $i$ and column $j$
$m_{i, j} = | \begin{array}{llllll} a_{11} & \dots & a_{1, j - 1} & a_{1, j + 1} & \dots & a_{1, m} \\ ⋮ & \dots & ⋮ & ⋮ & \dots & ⋮ \\ a_{i - 1, 1} & \dots & a_{i - 1, j - 1} & a_{i - 1, j + 1} & \dots & a_{i - 1, m} \\ a_{i + 1, 1} & \dots & a_{i + 1, j - 1} & a_{i + 1, j + 1} & \dots & a_{i + 1, m} \\ ⋮ & \dots & ⋮ & ⋮ & \dots & ⋮ \\ a_{m, 1} & \dots & a_{m, j - 1} & a_{m, j + 1} & \dots & a_{m, m} \end{array} |$
The $(i, j)$ -cofactor of $𝑨$ is
$c_{i, j} = {(- 1)}^{i + j} m_{i, j}$
Minors and cofactors are useful in determinant calculations

Determinant expansion

A determinant of size $m$ can be expressed as a sum of determinants of size $m - 1$ by expansion along a row or column
$\begin{array}{rcl} | \begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \dots & a_{1 m} \\ a_{21} & a_{22} & a_{23} & \dots & a_{2 m} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m 1} & a_{m 2} & a_{m 3} & \dots & a_{m m} \end{array} | & = & a_{11} | \begin{array}{cccc} a_{22} & a_{23} & \dots & a_{2 m} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m 2} & a_{m 3} & \dots & a_{m m} \end{array} | - \\ a_{12} | \begin{array}{cccc} a_{21} & a_{23} & \dots & a_{2 m} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m 1} & a_{m 3} & \dots & a_{m m} \end{array} | + \\ \dots \\ + {(- 1)}^{m + 1} a_{1 m} | \begin{array}{cccc} a_{21} & a_{23} & \dots & a_{2, m - 1} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m 1} & a_{m 3} & \dots & a_{m, m - 1} \end{array} | \end{array}$
Expressed as cofactors $\det (𝑨) = \sum_{j = 1}^{m} a_{1 j} c_{1 j}$
In general $\det (𝑨) = \sum_{j = 1}^{m} a_{i, j} c_{i, j} = \sum_{i = 1}^{m} a_{i, j} c_{i, j}$

Determinant calculations by Gaussian elimination

Determinant rule
$\det (\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{m} \end{array}) = \det (\begin{array}{cccc} 𝒂_{1} & α 𝒂_{1} + 𝒂_{2} & \dots & 𝒂_{m} \end{array})$
means that Gaussian elimination operations can be used to compute $\det (𝑨)$
Approach:
- carry out linear combination of rows to reduce $𝑨$ to triangular form
  $\det (𝑨) = \det (𝑼)$
- The determinant of a triangular matrix is simply the product of its diagonal elements due to cofactor expansion
  $\det (𝑼) = | \begin{array}{llll} u_{11} & u_{12} & \dots & u_{1, m} \\ 0 & u_{22} & \dots & u_{2, m} \\ ⋮ & ⋮ & ⋱ \\ 0 & 0 & \dots & u_{m, m} \end{array} | = u_{11} | \begin{array}{lll} u_{22} & \dots & u_{2, m} \\ ⋮ & ⋱ \\ 0 & \dots & u_{m, m} \end{array} | = u_{11} u_{22} \dots u_{mm}$
The above leads to $𝒪 (m^{3} / 3)$ FLOPs computations for a determinant

Determinant of transpose, matrix product, non-full rank matrices

$\det (𝑨) = \det (𝑨^{T})$

Proof: After presentation of SVD
$\det (𝑨 𝑩) = \det (𝑨) \det (𝑩)$

Proof: After presentation of SVD
$𝑨 \in ℝ^{m \times m}$ , if $rank (𝑨) < m$ then $\det (𝑨) = 0$

Motivation: Some of the column vectors are linearly dependent

Algebraic definition of determinant

The formal definition of a determinant
$\det A = \sum_{σ \in Σ} ν (σ) a_{1 i_{1}} a_{2 i_{2}} \dots a_{m i_{m}}$
requires $m m!$ operations, a number that rapidly increases with $m$
A more economical determinant is to use row and column combinations to create zeros and then reduce the size of the determinant, an algorithm reminiscent of Gauss elimination for systems

Example:
$| \begin{array}{ccc} 1 & 2 & 3 \\ - 1 & 0 & 1 \\ - 2 & - 1 & 4 \end{array} | = | \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 3 & 10 \end{array} | = | \begin{array}{cc} 2 & 4 \\ 3 & 10 \end{array} | = 20 - 12 = 8$
The first equality comes from linear combinations of rows, i.e. row 1 is added to row 2, and row 1 multiplied by 2 is added to row 3. These linear combinations maintain the value of the determinant. The second equality comes from expansion along the first column

Cramer's rule to solve

𝑨 𝒙 = 𝒃

We've seen examples of “good” algorithms to solve a linear system ( $L U$ , $Q R$ )
The above find a solution using $𝒪 (m^{3} / 2)$ , $𝒪 (m^{3} / 2)$ FLOPS
Consider now an example of a “bad” algorithm, known as Cramer's rule
$x_{i} = \frac{Δ_{i}}{Δ}$
$Δ = \det (𝑨)$ is the principal determinant of the linear system
$Δ_{i} = \det ([\begin{array}{lllllll} 𝒂_{1} & \dots & 𝒂_{i - 1} & 𝒃 & 𝒂_{i + 1} & \dots & 𝒂_{m} \end{array}])$ arises from minors of $𝑨$
Why bad? It requires computation of $m + 1$ determinants, each of which costs $𝒪 (m^{3} / 3)$ leading to $𝒪 (m^{4} / 3)$ overall
Could be even worse! Before ubiquity of computers, determinants were often computed by the algebraic definition
$\det A = \sum_{σ \in Σ} ν (σ) a_{1 i_{1}} a_{2 i_{2}} \dots a_{m i_{m}}$
There are $m!$ terms in the sum. Each term costs $m$ flops. Using this in Cramer's rule gives $𝒪 (m^{2} m!)$ an incredibly large number for even small $m$ .