MATH347

MATH347 L18: Geometric applications of determinants

New concepts:
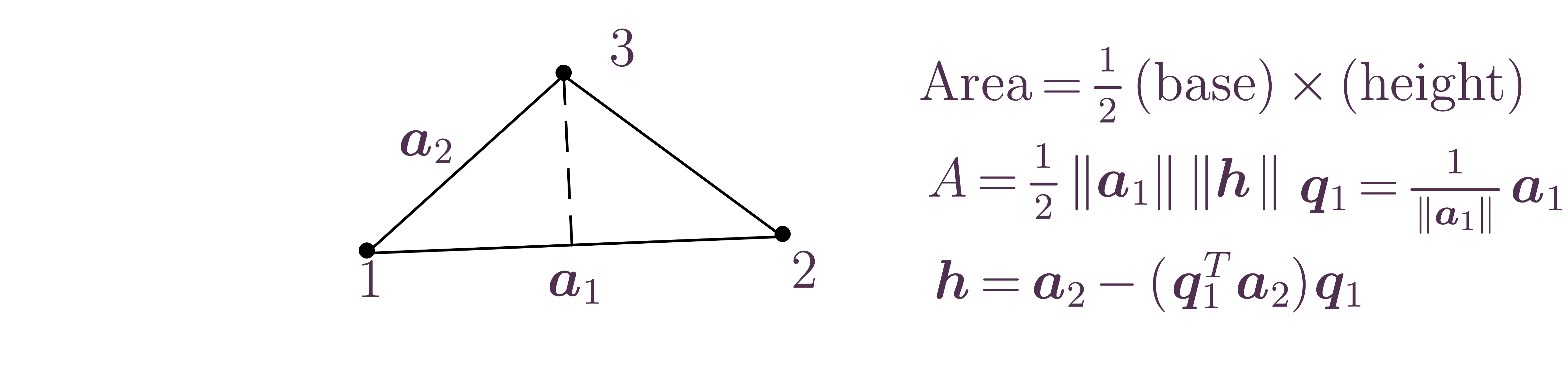
- Simplicia - simplest geometric object in $m$ dimensions
- Volumes of simplicia
- Volumes of complicated objects

Application of determinants: lengths, areas, volumes

$d = 1$ , define an interval by ${𝒓_{1}, 𝒓_{2}}$ , with $𝒓_{1}, 𝒓_{2} \in ℝ$ , $𝒓_{1} = (x_{1})$ , $𝒓_{2} = (x_{2})$ . The signed length of the interval is $l = x_{2} - x_{1}$ and can be computed as
$Δ = | \begin{array}{cc} 1 & 1 \\ x_{1} & x_{2} \end{array} |$
$d = 2,$ , define a triangle by ${𝒓_{1}, 𝒓_{2}, 𝒓_{3}}$ , with $𝒓_{1}, 𝒓_{2}, 𝒓_{3} \in ℝ^{2}$ . The signed area is
$Δ = \frac{1}{2} | \begin{array}{ccc} 1 & 1 & 1 \\ x_{1} & x_{2} & x_{3} \\ y_{1} & y_{2} & y_{3} \end{array} |$
$d = 3$ , define a tetrahedron by ${𝒓_{1}, 𝒓_{2}, 𝒓_{3}, 𝒓_{4}}$ . The signed volume is
$Δ = \frac{1}{6} | \begin{array}{cccc} 1 & 1 & 1 & 1 \\ x_{1} & x_{2} & x_{3} & x_{4} \\ y_{1} & y_{2} & y_{3} & y_{4} \\ z_{1} & z_{2} & z_{3} & z_{4} \end{array} |$

Example: How big is the hide on that cow?

octave>

cd ~/courses/MATH347/ply;

octave>

[x,tri]=ply_to_tri_mesh('cow.ply'); tri=transpose(tri);

octave>

trisurf(tri, x(1,:), x(2,:), x(3,:) ); print -dpng cow.png;

octave>

tri(:,100)

ans = 88 87 101

How big is the hide on that cow?

octave>

Area=0.;

octave>

for n=1:max(size(tri))
  n1=tri(1,n); n2=tri(2,n); n3=tri(3,n);
  a1 = x(:,n2)-x(:,n1); a2 = x(:,n3)-x(:,n1);
  q1 = a1/norm(a1); h = a2 - (q1'*a2)*q1;
  base = norm(a1); height = norm(h);
  Area = Area + 0.5*base*height;
end;

octave>

Area

Ahide = 21.193

How big is that cow?

octave>

tet=delaunay(x(1,:),x(2,:),x(3,:));

octave>

Volume=0.;

octave>

for n=1:max(size(tet))
  n1=tet(n,1); n2=tet(n,2); n3=tet(n,3); n4=tet(n,4);
  X = [x(:,n1) x(:,n2) x(:,n3) x(:,n4)];
  A = [ones(1,4); X];
  Volume = Volume + abs(det(A))/6.;
end;

octave>

Volume

Volume = 10.647

Volume = \frac{1}{6} | \begin{array}{cccc} 1 & 1 & 1 & 1 \\ x_{1} & x_{2} & x_{3} & x_{4} \\ y_{1} & y_{2} & y_{3} & y_{4} \\ z_{1} & z_{2} & z_{3} & z_{4} \end{array} |

Less whimsical example

Medical imaging (CT-scans) leads to extensive geometrical information

Figure 1. Left: CT scan of brain slice. Center: Brain regions. Right: Regions triangulation

Periodic high-resolution CT-scans are processed to evaluate brain volume as needed for instance in Alzheimer monitoring