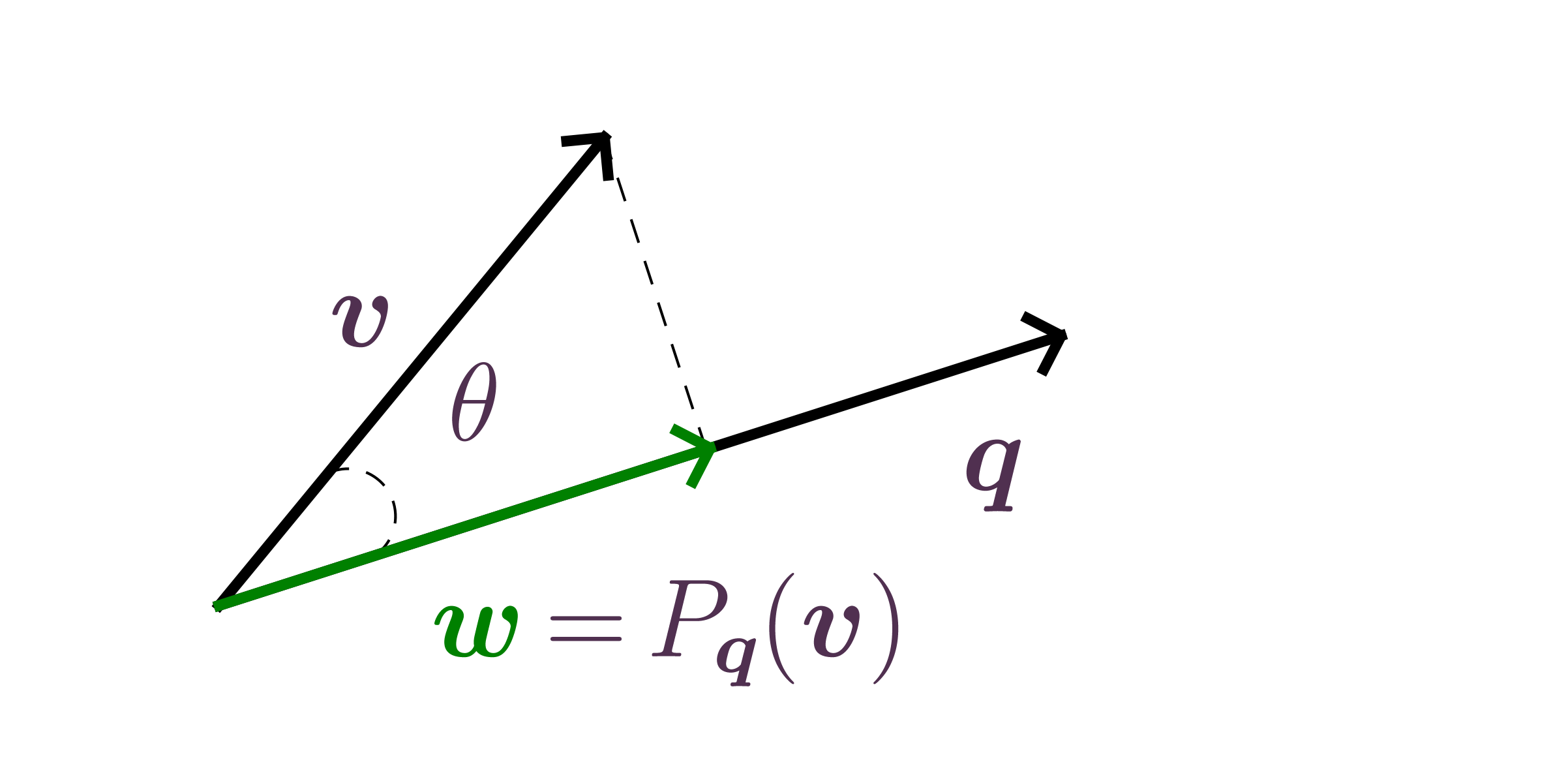New concepts:

• Projection review, projection onto subspaces

• Best approximation

• LSQ through projection

• LSQ solution by normal equations

Orthogonal projection of $𝒗\in {ℝ}^m$ along direction $𝒒\in {ℝ}^m$, $||𝒒||=1$

Figure 1. Orthogonal projection operation $P_{𝒒}$.

$𝒘=(||𝒗||\cos \theta )𝒒=(||𝒗||)𝒒=({𝒒}^T𝒒)𝒒=𝒒\left({𝒒}^T𝒗\right)=(𝒒{𝒒}^T)𝒗\Rightarrow$

Projection matrix ${𝑷}_{𝒒}=𝒒{𝒒}^T$ ($||𝒒||=1$)

Simple example: projection in ${ℝ}^3$ onto $x_1{x}_2$-plane of $𝒗\in {ℝ}^3$

The projection of $𝒗$ onto $x_1{x}_2$ plane is $𝒘=v_1{𝒆}_1+v_2{𝒆}_2=\left[\begin{array}{l}{v}_1\\ v_2\\ 0\end{array}\right]$

Projection is linear mapping, hence $𝒘={𝑷}_{12}𝒗$

Recall definition of orthonormal vectors

Columns of $𝑸=\left[\begin{array}{lll}{𝒒}_1& \dots & {𝒒}_n\end{array}\right]\in {ℝ}^{m\times n}$ are orthonormal if

Consider $C\left(𝑸\right)$ with $$$𝑸=\left[\begin{array}{lll}{𝒒}_1& \dots & {𝒒}_n\end{array}\right]\in {ℝ}^{m\times n}$ orthonormal. The matrix

is the standard matrix of the orthogonal projection of a vector in ${ℝ}^m$ onto the subspace spanned by {$\begin{array}{lll}{𝒒}_1& \dots & {𝒒}_n\end{array}$}, namely $C\left(𝑸\right)$.

Consider approximating $𝒃\in {ℝ}^m$ by linear combination of $n$ vectors, $𝑨\in {ℝ}^{m\times n}$

Make approximation error $𝒆=𝒃-𝒗=𝒃-𝑨𝒙$ as small as possible

Error is measured in the 2-norm $\Rightarrow$ the least squares problem (LSQ)

Solution is the projection of $𝒃$ onto $C\left(𝑨\right)$

The vector $𝒙$ is found by back-substitution from

The best approximant is found when the error vector $𝒆$ is orthogonal to $C\left(𝑨\right)$

The system $({𝑨}^T𝑨)𝒙={𝑨}^T𝒃$ is the normal system of the LSQ problem

Note that ${𝑨}^T𝑨\in {ℝ}^{n\times n}$