MATH347 L21: Eigenvalue problems
|
-
New concepts:
-
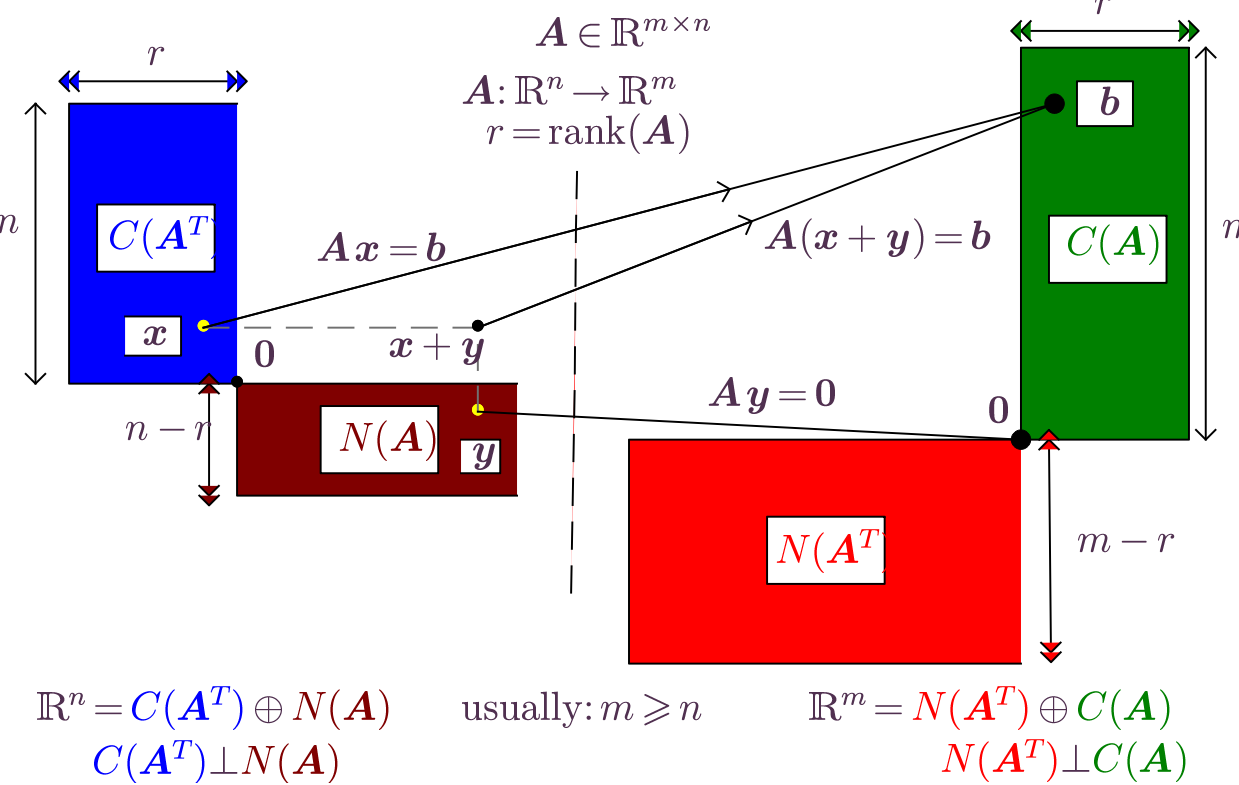
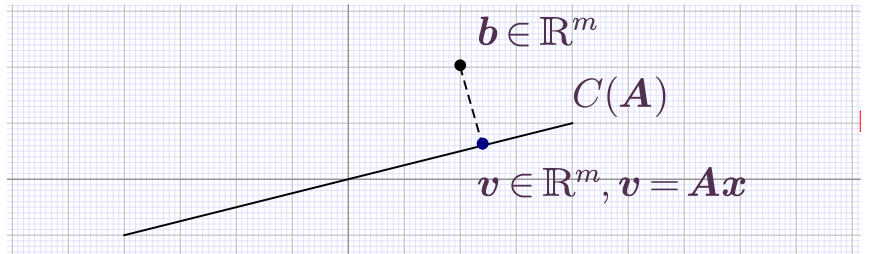
The eigenvalue problem as one of the principal problems of linear algebra
-
Eigenvalues and eigenvectors
-
Characteristic polynomial
-
Simple cases
-
diagonal matrices
-
scaling matrices
-
reflection matrices
-
rotation matrices (complex eigenvalues, eigenvectors)
-
-