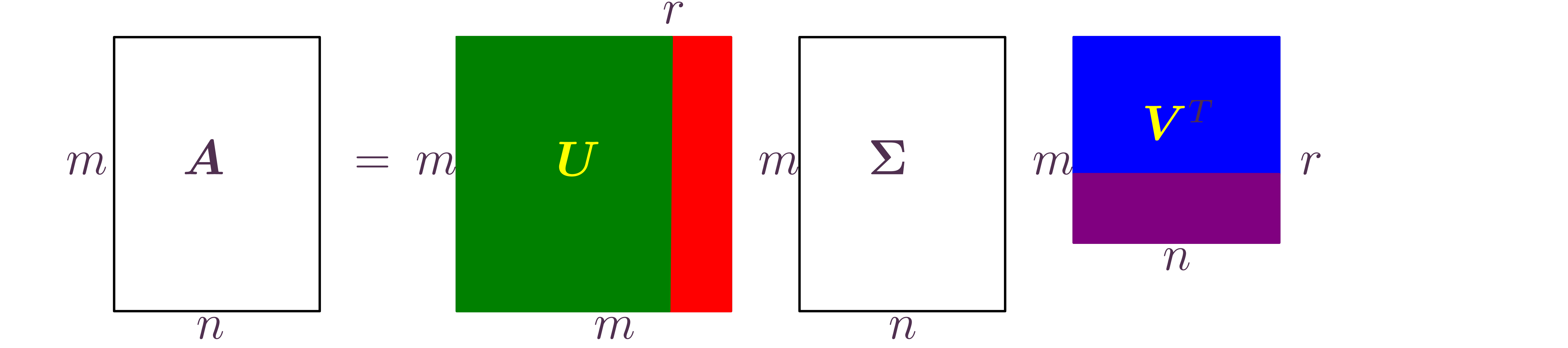MATH347 L23: Schur, singular value decompositions

• New concepts:

  • An orthogonal eigenvalue-revealing decomposition: Schur

  • Computability

  • Non-computability of polynomial roots

  • The need for an additional orthogonal decomposition

  • Interpreting the eigenvalue decomposition

  • Motivating the singular value decomposition

  • The singular value decomposition (SVD)

The most common matrix factorizations

• Review of alread encountered matrix decompositions:

  • $𝑳𝑼=𝑨$ factorization (Gaussian elimination), used to solve linear systems (compute coordinates in new basis)

  • $𝑸𝑹=𝑨$ factorization (Gram-Schmidt algorithm), used to solve least squares problems (compute best possible approximation)

  • $𝑨𝑿=𝑿𝚲$, eigenproblem. If $𝑿$ nonsingular, eigendecomposition $𝑿𝚲{𝑿}^{-1}=𝑨$ (reduction to diagonal form)

• Additional matrix decompositions:

  • $𝑸𝑻{𝑸}^T=𝑨$, Schur decomposition (reduction to triangular form)

  • $𝑷𝑱{𝑷}^{-1}=𝑨$, Jordan decomposition (reduction to disjoint eigenspaces)

  • $𝑼𝚺{𝑽}^T=𝑨$, singular value decomposition (SVD, reduction to diagonal form, but with different bases in the domain, codomain)

The Schur theorem

Theorem. (Schur) Any square matrix $𝑨\in {ℝ}^{m\times m}$ can be decomposed as $𝑨=𝑸𝑻{𝑸}^T$, with $𝑻\in {ℝ}^{m\times m}$ upper triangular ($t_{ij}=0$ for $i>j$) and $𝑸\in {ℝ}^{m\times m}$ orthogonal ($𝑸{𝑸}^T=𝑰$).

• The eigenvalues of $𝑻$ triangular are its diagonal elements

• $𝑨$ is similar to $𝑻$: $𝑨𝒙=\lambda 𝒙\Rightarrow 𝑻𝒚=\lambda 𝒚$ and $𝒚={𝑸}^T𝒚$

Computability.

• roots of first degree polynomial: $p_1\left(x\right)=ax+b=0\Rightarrow x=-b/a(a\ne 0)$

• roots of second degree polynomia: $p_2\left(x\right)=a{x}^2+bx+c\Rightarrow$

  ${\displaystyle x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}}$

• roots of third degree polynomial (Cardano's formulas ~1520's)

• roots of fourth degree polynomial (Ferrari's formulas ~1540's, irrespective of Inquisitor Torquemada forbidding Valmes such knowledge)

• fifth degree polynomial: no formula possible (Galois, Abel Ruffini, 1820's)

Interpreting the orthogonal eigendecompositions

• If $𝑨\in {ℝ}^{m\times m}$ is normal ($𝑨{𝑨}^T={𝑨}^T𝑨$) then it has an orthogonal eigendecomposition $\exists 𝑸,𝑨=𝑸𝚲{𝑸}^T,𝑸{𝑸}^T={𝑸}^T𝑸=𝑰$

• How does $𝒃=𝑨𝒙$ work?

  ${\displaystyle 𝒃=𝑨𝒙=𝑸𝚲{𝑸}^T𝒙=𝑸𝚲𝒚=𝑸𝒘}$ ${\displaystyle 𝒄={𝑸}^T𝒃\iff 𝑸𝒄=𝑰𝒃,𝒚={𝑸}^T𝒙\iff 𝑸𝒚=𝑰𝒙}$

• In the $𝑰=\left[\begin{array}{lll}{𝒆}_1& \dots & {𝒆}_m\end{array}\right]$ basis set $𝒃=x_1{𝒂}_1+\cdots +x_m{𝒂}_m$ implies all components of ${𝒂}_1,\dots ,{𝒂}_m$ influence each component of $𝒃$

  ${\displaystyle b_i=\sum _{j=1}^m{a}_{ij}{x}_j}$

• In the $𝑸$ basis set $𝒘=𝚲𝒚$, component $i$ of $𝒘$ influenced only by component $i$ of $𝒚$

  ${\displaystyle w_i={\lambda }_i{y}_i}$

Extend the idea: singular value decomposition

• For $𝑨\in {ℝ}^{m\times n}$, $𝒃=𝑨𝒙$, a mapping from ${ℝ}^n$ to ${ℝ}^m$ try to define:

  • an orthonormal basis $𝑽$ in ${ℝ}^n$, $𝑽\in {ℝ}^{n\times n}$, $𝑽{𝑽}^T={𝑽}^T𝑽={𝑰}_n$

    ${\displaystyle 𝑰𝒙=𝑽𝒚\Rightarrow 𝒚={𝑽}^T𝒙}$

  • an orthonormal basis $𝑼$ in ${ℝ}^m$, $𝑼\in {ℝ}^{m\times m}$, $𝑼{𝑼}^T={𝑼}^T𝑼={𝑰}_m$

    ${\displaystyle 𝑰𝒃=𝑼𝒄\Rightarrow 𝒄={𝑼}^T𝒃}$

  • impose that the action of $𝑨$ in the new bases is a simple component scaling

    ${\displaystyle 𝒄=𝚺𝒚\Rightarrow {𝑼}^T𝒃=𝚺{𝑽}^T𝒙\Rightarrow 𝒃=𝑼𝚺{𝑽}^T𝒙\Rightarrow }$ ${\displaystyle 𝑨=𝑼𝚺{𝑽}^T}$

  • Note that $𝚺\in {ℝ}^{m\times n}$

Can it be done? Yes: Singular value decomposition theorem

Theorem. (SVD) For any $𝑨\in {ℝ}^{m\times n}$, $𝑨=𝑼𝚺{𝑽}^T$, with $𝑼\in {ℝ}^{m\times m}$, $𝑽\in {ℝ}^{n\times n}$ orthogonal, $𝚺\in {ℝ}_{+}^{m\times n}$ pseudo-diagonal $𝚺=\mathrm{diag}({\sigma }_1,\dots ,{\sigma }_r,\dots ,0)$, ${\sigma }_1⩾{\sigma }_2⩾\cdots ⩾{\sigma }_r>0$, $r⩽min(m,n)$. $r=\mathrm{rank}\left(𝑨\right)$.

The SVD is determined by eigendecomposition of ${𝑨}^T𝑨$, and $𝑨{𝑨}^T$

• ${𝑨}^T𝑨={(𝑼𝚺{𝑽}^T)}^T(𝑼𝚺{𝑽}^T)=𝑽({𝚺}^T𝚺){𝑽}^T$, an eigendecomposition of ${𝑨}^T𝑨$. The columns of $𝑽$ are eigenvectors of ${𝑨}^T𝑨$ and called right singular vectors of $𝑨$

• $𝑨{𝑨}^T=(𝑼𝚺{𝑽}^T){(𝑼{𝚺}^T{𝑽}^T)}^T=𝑼\left(𝚺{𝚺}^T\right){𝑼}^T$, an eigendecomposition of $𝑨{𝑨}^T$. The columns of $𝑼$ are eigenvectors of $𝑨{𝑨}^T$ and called left singular vectors of $𝑨$

• The matrix $𝚺$ has zero elements except for the diagonal that contains ${\sigma }_i$, the singular values of $𝑨$, computed as the square roots of the eigenvalues of ${𝑨}^T𝑨$ (or $𝑨{𝑨}^T$)

The theorem also holds for complex matrices with transposition replaced by taking the adjoint, $𝑨\in {ℂ}^{m\times n}$, $𝑨=𝑼𝚺{𝑽}^{\ast }$, with $𝑼\in {ℂ}^{m\times m}$, $ℂ\in {ℝ}^{n\times n}$ unitary.

An all-encompassing diagram: SVD and matrix subspaces

• SVD of $𝑨\in {ℝ}^{m\times n}$ reveals: $\mathrm{rank}\left(𝑨\right)$, bases for $C\left(𝑨\right),N\left({𝑨}^T\right),C\left({𝑨}^T\right),N\left(𝑨\right)$