MATH347: Linear algebra for applicationsApril 28, 2024

Solve the following problems (5 course points each). Present a brief motivation of your method of solution. Problems 9 and 10 are optional; attempt them if you wish to improve your midterm examination score.

1. State the matrix product to obtain 3 linear combinations of vectors

   ${\displaystyle 𝒖=\left[\begin{array}{l}1\\ 0\\ 1\end{array}\right],𝒗=\left[\begin{array}{l}-1\\ 0\\ 1\end{array}\right],}$

   with scaling coefficients $({\alpha }_1,{\beta }_1)=(1,1)$, $({\alpha }_2,{\beta }_2)=(-1,1)$, $({\alpha }_3,{\beta }_3)=(1,-1)$.

   Solution. The matrix product is $𝑪=𝑨𝑩$, $𝑪\in {ℝ}^{3\times 3}$ (3 linear combinations, each with 3 components), $𝑨=\left[\begin{array}{ll}𝒖& 𝒗\end{array}\right]\in {ℝ}^{3\times 2}$ (vectors entering into linear combination), $𝑩\in {ℝ}^{2\times 3}$ (scaling coefficients of each linear combination)

   ${\displaystyle 𝑨=\left[\begin{array}{ll}1& -1\\ 0& 0\\ 1& 1\end{array}\right],𝑩=\left[\begin{array}{lll}1& -1& 1\\ 1& 1& -1\end{array}\right].}$

2. Orthonormalize the vectors

   ${\displaystyle 𝒖=\left[\begin{array}{l}1\\ 0\\ 1\end{array}\right],𝒗=\left[\begin{array}{l}-1\\ 0\\ 1\end{array}\right],𝒘=\left[\begin{array}{l}1\\ 1\\ -1\end{array}\right].}$

   Solution. Note that ${𝒖}^T𝒗={𝒖}^T𝒘=0$, such that these vector pairs are already orthogonal. Also note that the vector ${𝒆}_2={\left[\begin{array}{lll}0& 1& 0\end{array}\right]}^T$ is orthogonal to both $𝒖$ and $𝒗$. Scale vectors to have unit norm

   ${\displaystyle 𝑸=\left[\begin{array}{lll}{𝒒}_1& {𝒒}_2& {𝒒}_3\end{array}\right]=\left[\begin{array}{lll}𝒖/\sqrt{2}& 𝒗/\sqrt{2}& {𝒆}_2\end{array}\right].}$

3. For $x,y\in ℝ$, expansion of ${(x-y)}^3$ leads to ${(x-y)}^3=x^3-3x^{2}y+3x{y}^2-y^3$. Find the corresponding expansion of ${(𝑨-𝑩)}^3$ for $𝑨,𝑩\in {ℝ}^{m\times m}$.

   Solution. Compute, recalling that matrix multiplication is not commutative

   ${\displaystyle {(𝑨-𝑩)}^3=(𝑨-𝑩)({𝑨}^2-𝑨𝑩-𝑩𝑨+{𝑩}^2)={𝑨}^3-{𝑨}^2𝑩-𝑨𝑩𝑨+𝑨{𝑩}^2-𝑩{𝑨}^2+𝑩𝑨𝑩+{𝑩}^2-{𝑩}^3.}$

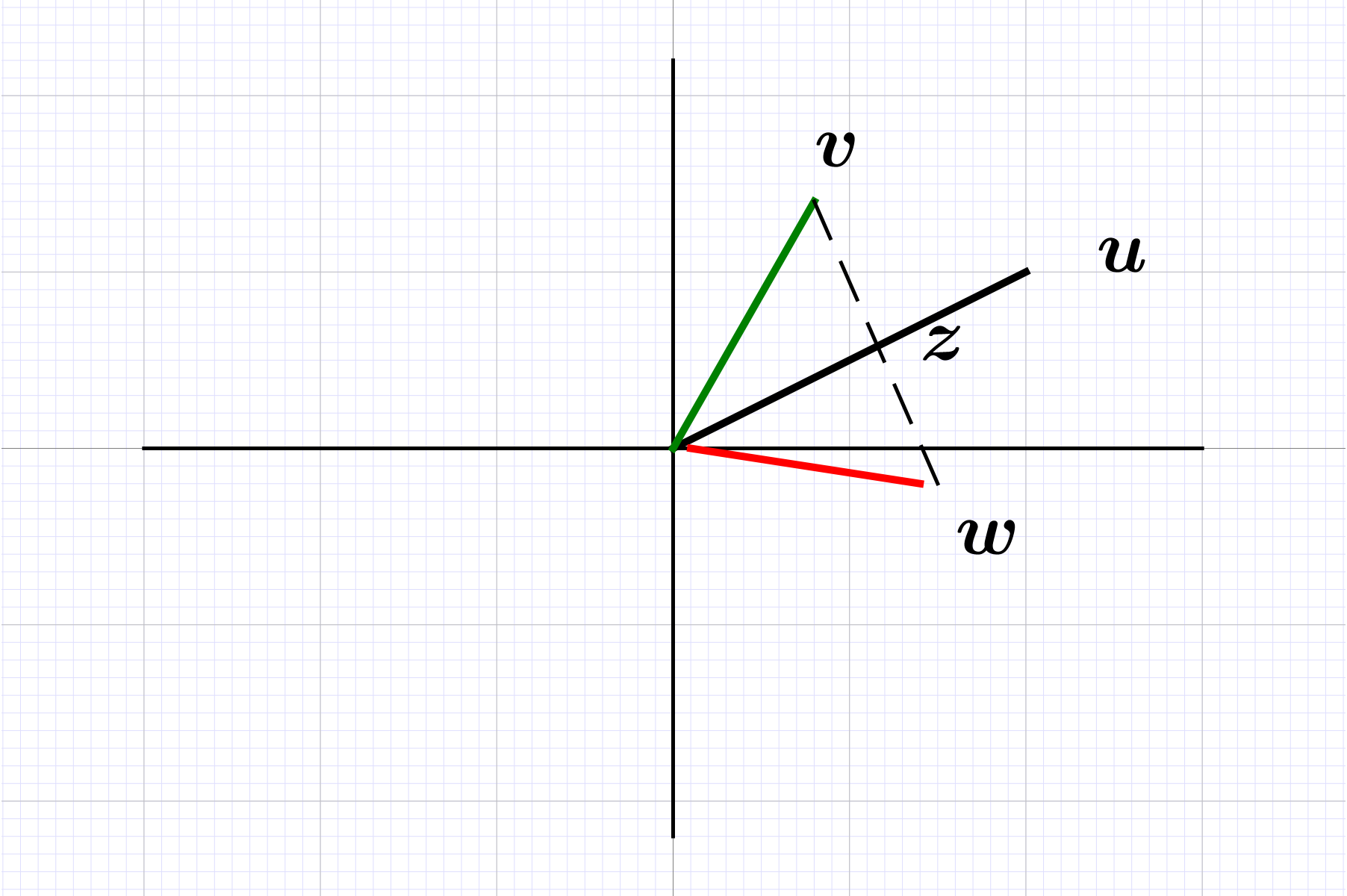
4. Find the projection of $𝒃$ onto $C\left(𝑨\right)$ for

   ${\displaystyle 𝒃=\left[\begin{array}{l}1\\ 2\\ 3\end{array}\right],𝑨=\left[\begin{array}{ll}1& -1\\ 1& 0\\ 1& 1\end{array}\right].}$

   Solution. With $𝑨=\left[\begin{array}{ll}{𝒂}_1& {𝒂}_2\end{array}\right]$ note that $𝒃=2{𝒂}_1+{𝒂}_2$, hence $𝒃\in C\left(𝑨\right)$, and the projection of $𝒃$ onto $C\left(𝑨\right)$ is $𝒃$ itself.

   Alternatively, orthonormalize $𝑨=\left[\begin{array}{ll}{𝒂}_1& {𝒂}_2\end{array}\right]$ to obtain

   ${\displaystyle 𝑸=\left[\begin{array}{ll}{𝒒}_1& {𝒒}_2\end{array}\right]=\left[\begin{array}{ll}{𝒂}_1/\sqrt{3}& {𝒂}_2/\sqrt{2}\end{array}\right].}$

   The projection onto $C\left(𝑨\right)$ is

   ${\displaystyle 𝒄=𝑸{𝑸}^T𝒃=𝑸({𝑸}^T𝒃)=\left[\begin{array}{ll}1/\sqrt{3}& -1/\sqrt{2}\\ 1/\sqrt{3}& 0\\ 1/\sqrt{3}& 1/\sqrt{2}\end{array}\right]\left(\left[\begin{array}{lll}1/\sqrt{3}& 1/\sqrt{3}& 1/\sqrt{3}\\ -1/\sqrt{2}& 0& 1/\sqrt{2}\end{array}\right]\left[\begin{array}{l}1\\ 2\\ 3\end{array}\right]\right)\Rightarrow }$
   ${\displaystyle 𝒄=\left[\begin{array}{ll}1/\sqrt{3}& -1/\sqrt{2}\\ 1/\sqrt{3}& 0\\ 1/\sqrt{3}& 1/\sqrt{2}\end{array}\right]\left[\begin{array}{l}2\sqrt{3}\\ \sqrt{2}\end{array}\right]=\left[\begin{array}{l}1\\ 2\\ 3\end{array}\right].}$

5. Find the $LU$ decomposition of

   ${\displaystyle 𝑨=\left[\begin{array}{lll}1& 1& 1\\ 2& 3& 3\\ 3& 5& 6\end{array}\right].}$

   Solution. Carry out reduction to upper triangular form, noting multipliers used in the process

   ${\displaystyle {𝑳}_1𝑨=\left[\begin{array}{lll}1& 0& 0\\ -2& 1& 0\\ -3& 0& 1\end{array}\right]\left[\begin{array}{lll}1& 1& 1\\ 2& 3& 3\\ 3& 5& 6\end{array}\right]=\left[\begin{array}{lll}1& 1& 1\\ 0& 1& 1\\ 0& 2& 3\end{array}\right].}$ ${\displaystyle {𝑳}_2{𝑳}_1𝑨=\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\\ 0& -2& 1\end{array}\right]\left[\begin{array}{lll}1& 1& 1\\ 0& 1& 1\\ 0& 2& 3\end{array}\right]=\left[\begin{array}{lll}1& 1& 1\\ 0& 1& 1\\ 0& 0& 1\end{array}\right]=𝑼.}$

   Find $𝑨={𝑳}_1^{-1}{𝑳}_2^{-1}𝑼=𝑳𝑼$. Compute

   ${\displaystyle 𝑳={𝑳}_1^{-1}{𝑳}_2^{-1}=\left[\begin{array}{lll}1& 0& 0\\ 2& 1& 0\\ 3& 0& 1\end{array}\right]\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\\ 0& 2& 1\end{array}\right]=\left[\begin{array}{lll}1& 0& 0\\ 2& 1& 0\\ 3& 2& 1\end{array}\right].}$

   Verify

   ${\displaystyle 𝑳𝑼=\left[\begin{array}{lll}1& 0& 0\\ 2& 1& 0\\ 3& 2& 1\end{array}\right]\left[\begin{array}{lll}1& 1& 1\\ 0& 1& 1\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{lll}1& 1& 1\\ 2& 3& 3\\ 3& 5& 6\end{array}\right].?}$

6. State the eigenvalues and eigenvectors of $𝑹\in {ℝ}^{2\times 2}$, the matrix describing reflection across the vector $𝒘={\left[\begin{array}{ll}1& 2\end{array}\right]}^T$.

   Solution. From eigenvalue relation $𝑹𝒙=\lambda 𝒙$ note that directions not changed by reflection are along $𝒘$ and orthogonal to $𝒘$. Deduce

   ${\displaystyle {𝒙}_1=𝒘=\left[\begin{array}{l}1\\ 2\end{array}\right],{\lambda }_1=1}$
   ${\displaystyle {𝒙}_2=𝒘=\left[\begin{array}{l}-2\\ 1\end{array}\right],{\lambda }_2=-1.}$

7. Compute the eigendecomposition of

   ${\displaystyle 𝑨=\left[\begin{array}{lll}5/2& 0& 1/2\\ 0& 1& 0\\ 1/2& 0& 5/2\end{array}\right].}$

   Solution. Eigenvalue problem is $𝑨𝒙=\lambda 𝒙$. Observe that ${𝒙}_2={𝒆}_2={\left[\begin{array}{lll}0& 1& 0\end{array}\right]}^T$, ${\lambda }_2=1$ is an eigenvector, value pair. Compute characteristic polynomial by

   ${\displaystyle p\left(\lambda \right)=\det (\lambda 𝑰-𝑨)=\left|\begin{array}{lll}\lambda -5/2& 0& -1/2\\ 0& \lambda -1& 0\\ -1/2& 0& \lambda -5/2\end{array}\right|=(\lambda -1)\left|\begin{array}{ll}\lambda -5/2& -1/2\\ -1/2& \lambda -5/2\end{array}\right|\Rightarrow }$ ${\displaystyle p\left(\lambda \right)=(\lambda -1)({\lambda }^2-5\lambda +{\left(\frac{5}{2}\right)}^2-{\left(\frac{1}{2}\right)}^2)=(\lambda -1)({\lambda }^2-5\lambda +6)=(\lambda -1)(\lambda -2)(\lambda -3).}$

   The other eigevalues are ${\lambda }_1=2$, ${\lambda }_3=3$. Find eigenvectors by computing bases for eigenspaces $N(𝑨-{\lambda }_1𝑰)$ and $N(𝑨-{\lambda }_3𝑰)$.

   ${\displaystyle 𝑨-{\lambda }_1𝑰=\left[\begin{array}{lll}1/2& 0& 1/2\\ 0& 1& 0\\ 1/2& 0& 1/2\end{array}\right]\sim \left[\begin{array}{lll}1/2& 0& 1/2\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]\Rightarrow {𝒙}_1=\left[\begin{array}{l}1\\ 0\\ -1\end{array}\right]}$
   ${\displaystyle 𝑨-{\lambda }_3𝑰=\left[\begin{array}{lll}-1/2& 0& 1/2\\ 0& 1& 0\\ 1/2& 0& -1/2\end{array}\right]\sim \left[\begin{array}{lll}-1/2& 0& 1/2\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]\Rightarrow {𝒙}_3=\left[\begin{array}{l}1\\ 0\\ 1\end{array}\right].}$

8. Find the SVD of

   ${\displaystyle 𝑨=\left[\begin{array}{ll}1& -1\\ 0& 0\\ 1& 1\end{array}\right].}$

   Solution. Matrix has orthogonal columns that are not of unit norm. Construct SVD as

   ${\displaystyle 𝑨=\left[\begin{array}{ll}1/\sqrt{2}& -1/\sqrt{2}\\ 0& 0\\ 1/\sqrt{2}& 1/\sqrt{2}\end{array}\right]\left[\begin{array}{ll}\sqrt{2}& 0\\ 0& \sqrt{2}\\ 0& 0\end{array}\right]\left[\begin{array}{ll}1& 0\\ 0& 1\end{array}\right].}$

9. Find the matrix of the reflection of ${ℝ}^2$ vectors across the vector $𝒖={\left[\begin{array}{ll}1& 2\end{array}\right]}^T$.

   Solution. Let $𝒘$ be the reflection of $𝒗$ across $𝒖$, $𝒘=𝑹𝒗$. Let

   ${\displaystyle 𝒒=\frac{1}{||𝒖||}𝒖=\frac{1}{\sqrt{5}}\left[\begin{array}{l}1\\ 0\end{array}\right].}$

   The projection of $𝒗$ onto the direction of $𝒖$ is $𝒛=𝒒{𝒒}^T𝒗$. The travel from $𝒗$ to $𝒛$ is $𝒛-𝒗$

   ${\displaystyle 𝒛=𝒗+(𝒛-𝒗).}$

   The reflection is obtained by doubling the travel distance

   ${\displaystyle 𝒘=𝒗+2(𝒛-𝒗)=2𝒛-𝒗=(2𝒒{𝒒}^T-𝑰)𝒗.}$

   Deduce that the reflection matrix is

   ${\displaystyle 𝑹=2𝒒{𝒒}^T-𝑰.}$

   Figure 1.

10. Find bases for the four fundamental spaces of

    ${\displaystyle 𝑨=\left[\begin{array}{ll}1& -1\\ 0& 0\\ 1& 1\end{array}\right].}$

    Solution. With $𝑨=\left[\begin{array}{ll}{𝒂}_1& {𝒂}_2\end{array}\right]\in {ℝ}^{3\times 2}$, the bases are:

    $C\left(𝑨\right)$: $\{{𝒂}_1,{𝒂}_2\}$

    $N\left({𝑨}^T\right)$: $\left\{{𝒆}_2\right\}$ since ${𝒆}_2$ is orthogonal to both ${𝒂}_1$ and ${𝒂}_2$

    $C\left({𝑨}^T\right)$: $\{{𝒂}_1^T,{𝒂}_2^T\}$

    $N\left(𝑨\right)$: $\left\{𝟎\right\}$