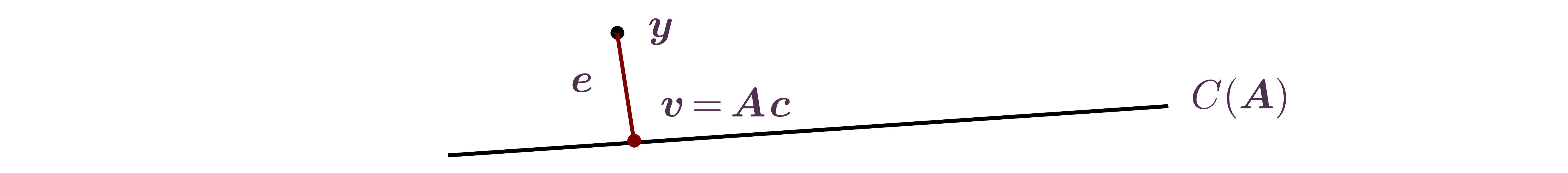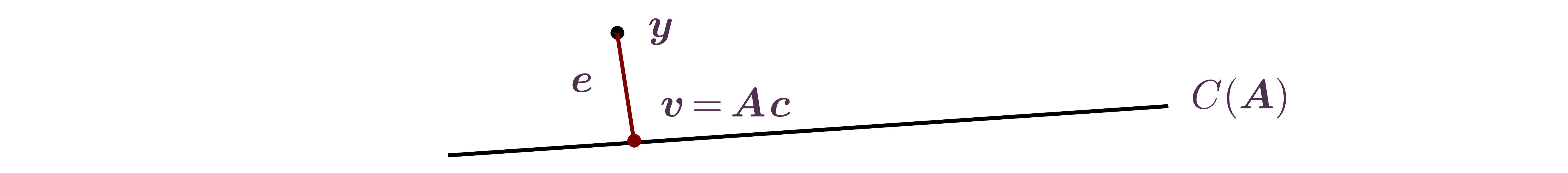MATH347DS

MATH347DS L05: The FTLA

Overview

FTLA-associated definitions and results
Main problems of linear algebra
Homework review
$𝑸 𝑹$ factorization (Gram-Schmidt algorithm)
Projection
Least-squares approach to polynomial approximation

Preparing the FTLS

Set $S$ partition = collection $P$ of disjoint subsets covering the entire set
$P = {S_{i} | S_{i} \subset P, S_{i} \neq \emptyset .}, \forall x \in S, \exists! S_{i} : x \in S_{i}$
Partitioning of vector spaces: similar allow $𝟎$ as a common element
$𝒇 : ℝ^{n} \to ℝ^{m}$ , $𝒇 (a 𝒙 + b 𝒚) = a 𝒇 (𝒙) + b 𝒇 (𝒚)$ ,
$𝑨 = [\begin{array}{cccc} 𝒇 (𝒆_{1}) & 𝒇 (𝒆_{2}) & \dots & 𝒇 (𝒆_{n}) \end{array}] = [\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}]$
Relationships of subspaces associated with $𝑨$
$\begin{array}{cccc} C (𝑨) \leq ℝ^{m}, & N (𝑨^{T}) \leq ℝ^{m}, & C (𝑨) ⊥ N (𝑨^{T}) & C (𝑨) + N (𝑨^{T}) \leq ℝ^{m} \end{array} .$

When is a vector space sum a direct sum?

Lemma 1. Let $𝒰, 𝒱$ , be subspaces of vector space $𝒲$ . Then $𝒲 = 𝒰 \oplus 𝒱$ if and only if

$𝒲 = 𝒰 + 𝒱$ , and

$𝒰 \cap 𝒱 = {𝟎}$ .

Proof. $𝒲 = 𝒰 \oplus 𝒱 \Rightarrow 𝒲 = 𝒰 + 𝒱$ by definition of direct sum, sum of vector subspaces. To prove that $𝒲 = 𝒰 \oplus 𝒱 \Rightarrow 𝒰 \cap 𝒱 = {𝟎}$ , consider $𝒘 \in 𝒰 \cap 𝒱$ . Since $𝒘 \in 𝒰$ and $𝒘 \in 𝒱$ write

$\begin{array}{llll} 𝒘 = 𝒘 + 𝟎 & (𝒘 \in 𝒰, 𝟎 \in 𝒱), & 𝒘 = 𝟎 + 𝒘 & (𝟎 \in 𝒰, 𝒘 \in 𝒱), \end{array}$

and since expression $𝒘 = 𝒖 + 𝒗$ is unique, it results that $𝒘 = 𝟎$ . Now assume (i),(ii) and establish an unique decomposition. Assume there might be two decompositions of $𝒘 \in 𝒲$ , $𝒘 = 𝒖_{1} + 𝒗_{1}$ , $𝒘 = 𝒖_{2} + 𝒗_{2}$ , with $𝒖_{1}, 𝒖_{2} \in 𝒰$ , $𝒗_{1}, 𝒗_{2} \in 𝒱 .$ Obtain $𝒖_{1} + 𝒗_{1} = 𝒖_{2} + 𝒗_{2}$ , or $𝒙 = 𝒖_{1} - 𝒖_{2} = 𝒗_{2} - 𝒗_{1}$ . Since $𝒙 \in 𝒰$ and $𝒙 \in 𝒱$ it results that $𝒙 = 𝟎$ , and $𝒖_{1} = 𝒖_{2}$ , $𝒗_{1} = 𝒗_{2}$ , i.e., the decomposition is unique. $□$

The FTLA

Theorem. Given the linear mapping associated with matrix $𝑨 \in ℝ^{m \times n}$ we have:

$C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ , the direct sum of the column space and left null space is the codomain of the mapping

$C (𝑨^{T}) \oplus N (𝑨) = ℝ^{n}$ , the direct sum of the row space and null space is the domain of the mapping

$C (𝑨) ⊥ N (𝑨^{T})$ and $C (𝑨) \cap N (𝑨^{T}) = {𝟎}$ , the column space is orthogonal to the left null space, and they are orthogonal complements of one another,
$\begin{array}{ll} C (𝑨) = N {(𝑨^{T})}^{⊥}, & N (𝑨^{T}) = C {(𝑨)}^{⊥} \end{array} .$

$C (𝑨^{T}) ⊥ N (𝑨)$ and $C (𝑨^{T}) \cap N (𝑨) = {𝟎}$ , the row space is orthogonal to the null space, and they are orthogonal complements of one another,
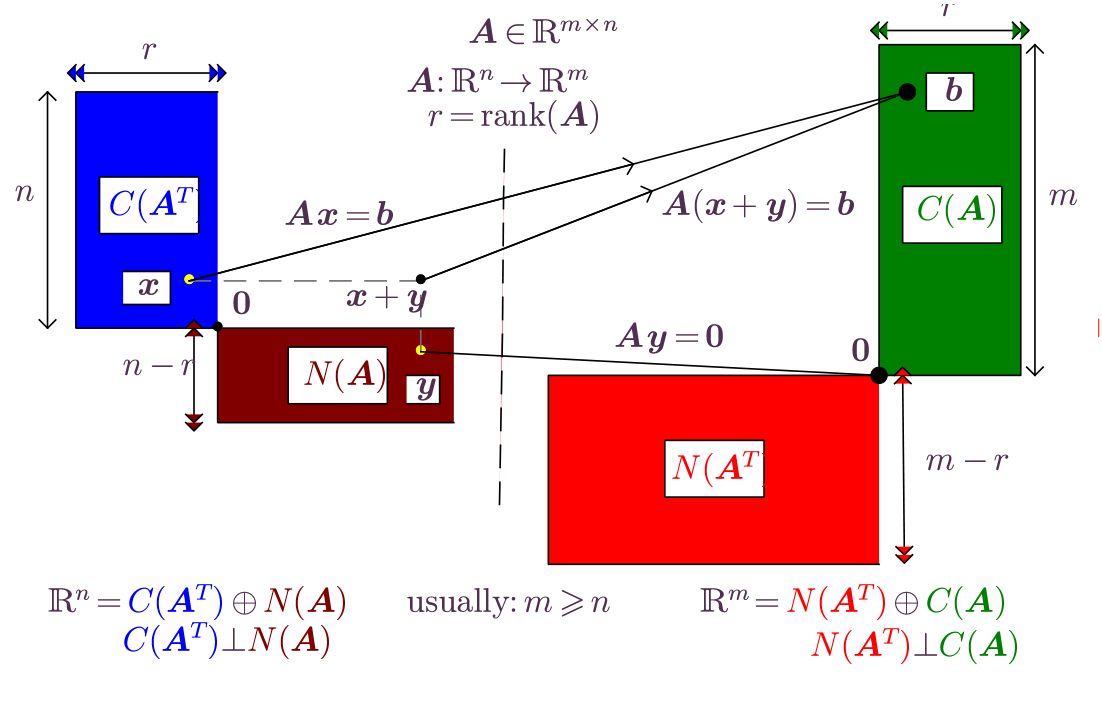
$\begin{array}{ll} C (𝑨^{T}) = N {(𝑨)}^{⊥}, & N (𝑨) = C {(𝑨^{T})}^{⊥} \end{array} .$

FTLA: a graphical representation

Figure 1. Graphical representation of the Fundamental Theorem of Linear Algebra, Gil Strang, Amer. Math. Monthly 100, 848-855, 1993.

FTLA: proof

FTLA proof highlights the properties of a norm, especially $|| 𝒖 || = 0 \Rightarrow 𝒖 = 𝟎$ .

$C (𝑨) ⊥ N (𝑨^{T})$ (column space is orthogonal to left null space).

Proof. Consider arbitrary $𝒖 \in C (𝑨), 𝒗 \in N (𝑨^{T})$ . By definition of $C (𝑨)$ , $\exists 𝒙 \in ℝ^{n}$ such that $𝒖 = 𝑨 𝒙$ , and by definition of $N (𝑨^{T})$ , $𝑨^{T} 𝒗 = 𝟎$ . Compute $𝒖^{T} 𝒗 = {(𝑨 𝒙)}^{T} 𝒗 = 𝒙^{T} 𝑨^{T} 𝒗 = 𝒙^{T} (𝑨^{T} 𝒗) = 𝒙^{T} 𝟎 = 0$ , hence $𝒖 ⊥ 𝒗$ for arbitrary $𝒖, 𝒗$ , and $C (𝑨) ⊥ N (𝑨^{T})$ . $□$
$C (𝑨) \cap N (𝑨^{T}) = {𝟎}$ ( $𝟎$ is the only vector both in $C (𝑨)$ and $N (𝑨^{T})$ ).

Proof. (By contradiction, reductio ad absurdum). Assume there might be $𝒃 \in C (𝑨)$ and $b \in N (𝑨^{T})$ and $𝒃 \neq 𝟎$ . Since $𝒃 \in C (𝑨)$ , $\exists 𝒙 \in ℝ^{n}$ such that $𝒃 = 𝑨 𝒙$ . Since $𝒃 \in N (𝑨^{T})$ , $𝑨^{T} 𝒃 = 𝑨^{T} (𝑨 𝒙) = 𝟎$ . Note that $𝒙 \neq 0$ since $𝒙 = 0 \Rightarrow 𝒃 = 0$ , contradicting assumptions. Multiply equality $𝑨^{T} 𝑨 𝒙 = 𝟎$ on left by $𝒙^{T}$ ,
$𝒙^{T} 𝑨^{T} 𝑨 𝒙 = 𝟎 \Rightarrow {(𝑨 𝒙)}^{T} (𝑨 𝒙) = 𝒃^{T} 𝒃 = {|| 𝒃 ||}^{2} = 0,$
thereby obtaining $𝒃 = 0$ , using norm property 3. Contradiction.

$□$

FTLA: proof

established that $C (𝑨), N (𝑨^{T})$ are orthogonal complements
$C (𝑨) = N {(𝑨^{T})}^{⊥}, N (𝑨^{T}) = C {(𝑨)}^{⊥} .$
By Lemma 2 it results that $C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ .
Second part of FTLA: as above for $𝑩 = 𝑨^{T}$

FTLA: useful concepts and results

FTLA in a mathematical nutshell: matrix $𝑨 \in ℝ^{m \times n}$ represents linear mapping $f : ℝ^{n} \to ℝ^{m}$
$\begin{array}{lll} C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m} & C (𝑨) ⊥ N (𝑨^{T}) & C (𝑨) \cap N (𝑨^{T}) = {𝟎} \\ C (𝑨^{T}) \oplus N (𝑨) = ℝ^{n} & C (𝑨^{T}) ⊥ N (𝑨) & C (𝑨^{T}) \cap N (𝑨) = {𝟎} \end{array}$

Definition. The rank of matrix $𝑨 \in ℝ^{m \times n}$ is the dimension of the column space, $r = \dim$ $C (𝑨)$

Definition. The nullity of $𝑨 \in ℝ^{m \times n}$ is the dimension of the null space, $z = \dim$ $C (𝑨)$

Proposition. The dimension of the column space equals the dimension of the row space.

Corollary. The system $𝑨 𝒙 = 𝒃$ , $𝑨 \in ℝ^{m \times n}$ , $𝒙 \in ℝ^{n}$ , $𝒃 \in ℝ^{m}$ has a solution if $𝒃 \in C (𝑨)$ . The solution is unique if $𝑵 (𝑨) = {𝟎}$ .

Orthonormal vector sets

Definition. The Dirac delta symbol $δ_{i j}$ is defined as

$δ_{i j} = {\begin{cases} 1 & if i = j \\ 0 & if i \neq j \end{cases}$

Definition. A set of vectors ${𝒖_{1}, \dots, 𝒖_{n}}$ is said to be orthonormal if

$𝒖_{i}^{T} 𝒖_{j} = δ_{i j}$

The column vectors of the identity matrix are orthonormal

𝑰 = (\begin{array}{ccc} 𝒆_{1} & \dots & 𝒆_{m} \end{array})

𝒆_{i}^{T} 𝒆_{j} = δ_{i j}

Gram-Schmidt algorithm

An arbitrary vector set can be transformed into an orthonormal set by the Gram-Schmidt algorithm
Idea:
- Start with an arbitrary direction $𝒂_{1}$
- Divide by its norm to obtain a unit-norm vector $𝒒_{1} = 𝒂_{1} / || 𝒂_{1} ||$
- Choose another direction $𝒂_{2}$
- Subtract off its component along previous direction(s) $𝒂_{2} - (𝒒_{1}^{T} 𝒂_{2}) 𝒒_{1}$
- Divide by norm $𝒒_{2} = (𝒂_{2} - (𝒒_{1}^{T} 𝒂_{2}) 𝒒_{1}) / || 𝒂_{2} - (𝒒_{1}^{T} 𝒂_{2}) 𝒒_{1} ||$
- Repeat the above

Matrix formulation of Gram-Schmidt (

𝑸 𝑹

factorization)

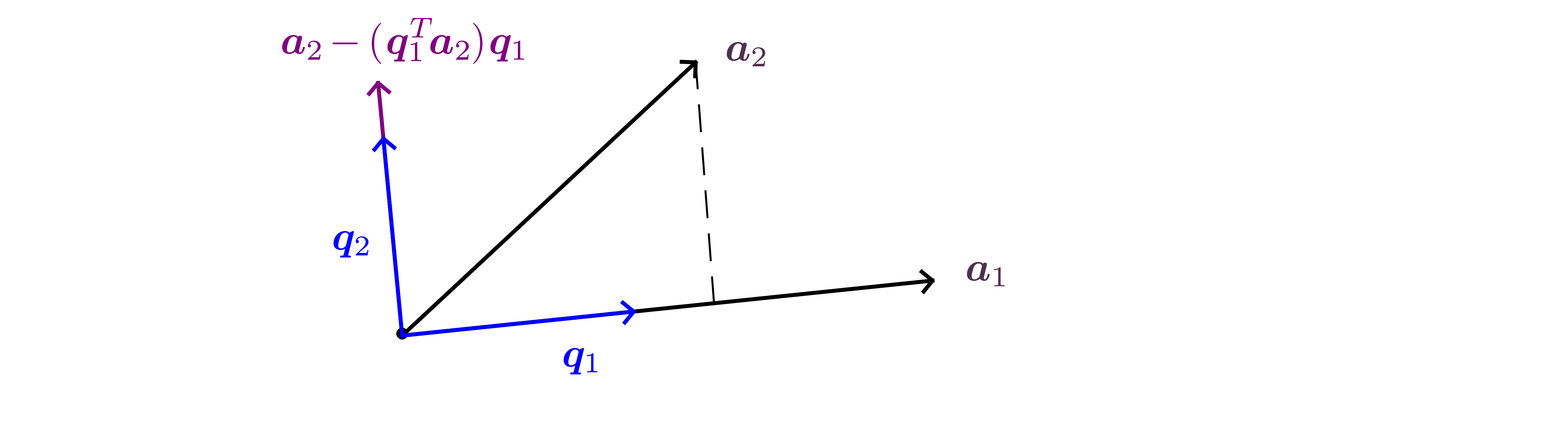
Consider $𝑨 \in ℝ^{m \times n}$ with linearly independent columns. By linear combinations of the columns of $𝑨$ a set of orthonormal vectors $𝒒_{1}, \dots, 𝒒_{n}$ will be obtained. This can be expressed as a matrix product
$𝑨 = (\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}) = (\begin{array}{cccc} 𝒒_{1} & 𝒒_{2} & \dots & 𝒒_{n} \end{array}) (\begin{array}{ccccc} r_{11} & r_{12} & r_{13} & \dots & r_{1 n} \\ 0 & r_{22} & r_{23} & \dots & r_{2 n} \\ 0 & 0 & r_{33} & \dots & r_{3 n} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & \dots & r_{m n} \end{array}) = 𝑸 𝑹$
with $𝑸 \in ℝ^{m \times n}$ , $𝑹 \in ℝ^{n \times n}$ . The matrix $𝑹$ is upper-triangular (also referred to as right-triangular) since to find vector $𝒒_{1}$ only vector $𝒂_{1}$ is used, to find vector $𝒒_{2}$ only vectors $𝒂_{1}, 𝒂_{2}$ are used
The above is equivalent to the system
${\begin{cases} 𝒂_{1} = r_{11} 𝒒_{1} \\ 𝒂_{2} = r_{12} 𝒒_{1} + r_{22} 𝒒_{2} \\ ⋮ \\ 𝒂_{n} = r_{1 n} 𝒒_{1} + r_{2 n} 𝒒_{2} + \dots + r_{n n} 𝒒_{n} \end{cases}$

Matrix formulation of Gram-Schmidt (

𝑸 𝑹

factorization)

The system can be solved to find $𝑹, 𝑸$ by:
1. Imposing $|| 𝒒_{1} || = 1 \Rightarrow r_{11} = || 𝒂_{1} ||$ , $𝒒_{1} = a_{1} / r_{11}$
2. Computing projections of $𝒂_{2}, \dots, 𝒂_{n}$ along $𝒒_{1}$
  $r_{12} = 𝒒_{1}^{T} 𝒂_{2}, \dots, r_{1 n} = 𝒒_{1}^{T} 𝒂_{n}$
3. Subtracting components along $𝒒_{1}$ from $𝒂_{2}, \dots, 𝒂_{n}$
  ${\begin{cases} 𝒂_{2} - r_{12} 𝒒_{1} = r_{22} 𝒒_{2} \\ ⋮ \\ 𝒂_{n} - r_{1 n} 𝒒_{1} = r_{2 n} 𝒒_{2} + \dots + r_{n n} 𝒒_{n} \end{cases}$
4. The above steps reduced the size of the system by 1. Repeating the steps completes the solution. The overall process is known as the Gram-Schmidt algorithm

Gram-Schmidt algorithm

Algorithm (Gram-Schmidt)

Given $n$ vectors $𝒂_{1}, \dots, 𝒂_{n} \in ℝ^{m}$

Initialize $𝒒_{1} = 𝒂_{1}$ ,.., $𝒒_{n} = 𝒂_{n}$ , $𝑹 = 𝑰_{n} \in ℝ^{n \times n}$

for $i = 1$ to $n$

$r_{i i} = {(𝒒_{i}^{T} 𝒒_{i})}^{1 / 2}$ ; $𝒒_{i} = 𝒒_{i} / r_{i i}$

for $j = i + 1$ to $n$

$r_{i j} = 𝒒_{i}^{T} 𝒂_{j}$ ; $𝒒_{j} = 𝒒_{j} - r_{i j} 𝒒_{i}$

end

return $𝑸, 𝑹$

𝑸 𝑹

factorization

For $𝑨 \in ℝ^{m \times n}$ with linearly independent columns, the Gram-Schmidt algorithm furnishes a factorization
$𝑸 𝑹 = 𝑨$
with $𝑸 \in ℝ^{m \times n}$ with orthonormal columns and $𝑹 \in ℝ^{n \times n}$ an upper triangular matrix.
Since the column vectors within $𝑸$ were obtained through linear combinations of the column vectors of $𝑨$ we have
$C (𝑨) = C (𝑸)$

Orthogonal projection of a vector along another vector

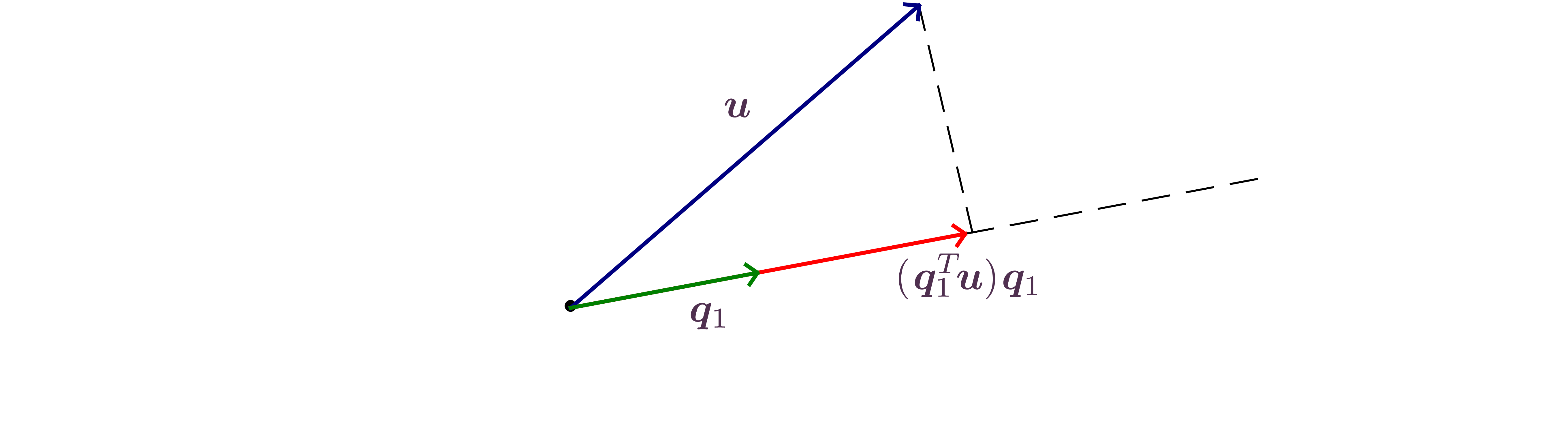
Consider a vector $𝒖 \in ℝ^{m}$ , and a unit-norm vector $𝒒_{1} \in ℝ^{m}$

Definition. The orthogonal projection of $𝒖 \in ℝ^{m}$ along direction $𝒒_{1} \in ℝ^{m}$ , $|| 𝒒_{1} || = 1$ is the vector $(𝒒_{1}^{T} 𝒖) 𝒒_{1}$ .

Scalar-vector multiplication commutativity: $(𝒒_{1}^{T} 𝒖) 𝒒_{1} = 𝒒_{1} (𝒒_{1}^{T} 𝒖)$
Matrix multiplication associativity: $𝒒_{1} (𝒒_{1}^{T} 𝒖) = (𝒒_{1} 𝒒_{1}^{T}) 𝒖 = 𝑷_{1} 𝒖$ , with $𝑷_{1} \in ℝ^{m \times m}$

Definition. The matrix $𝑷_{1} = 𝒒_{1} 𝒒_{1}^{T} \in ℝ^{m \times m}$ is the orthogonal projector along direction $𝒒_{1} \in ℝ^{m}$ , $|| 𝒒_{1} || = 1$ .

Orthogonal projection onto a subspace

Consider $n$ orthonormal vectors grouped into a matrix $𝑸 = (\begin{array}{lll} 𝒒_{1} & \dots & 𝒒_{n} \end{array}) \in ℝ^{m \times n}$

The orthogonal projection of $𝒖$ onto the subspace spanned by $𝒒_{1}, \dots, 𝒒_{n}$ is
$𝑷 𝒖 = 𝑷_{1} 𝒖 + \dots + 𝑷_{n} 𝒖 = (𝒒_{1} 𝒒_{1}^{T}) 𝒖 + \dots +_{} (𝒒_{n} 𝒒_{n}^{T}) 𝒖 \Rightarrow$ $𝑷 = 𝒒_{1} 𝒒_{1}^{T} + \dots + 𝒒_{n} 𝒒_{n}^{T} = (\begin{array}{ccc} 𝒒_{1} & \dots & 𝒒_{n} \end{array}) (\begin{array}{c} 𝒒_{1}^{T} \\ ⋮ \\ 𝒒_{n}^{T} \end{array}) = 𝑸 𝑸^{T}$

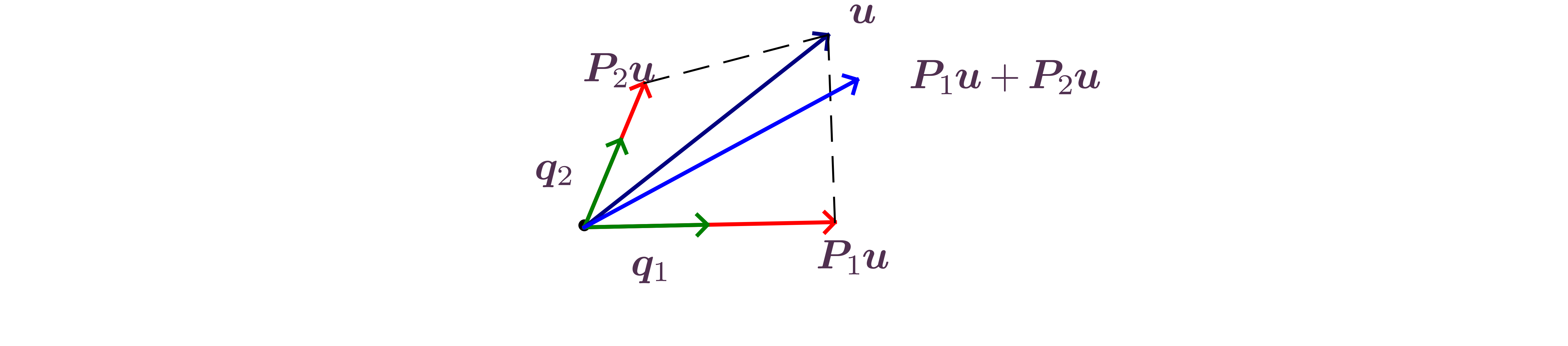
Definition. The orthogonal projector onto $C (𝑸)$ , $𝑸 \in ℝ^{m \times n}$ with orthonormal column vectors is $𝑷 = 𝑸 𝑸^{T}$

Complementary orthogonal projector

Given $𝒖 \in ℝ^{m}$ and $𝑸 = (\begin{array}{lll} 𝒒_{1} & \dots & 𝒒_{n} \end{array}) \in ℝ^{m \times n}$ with orthonormal columns

Definition. The complementary orthogonal projector to $𝑷 = 𝑸 𝑸^{T}$ is $𝑰 - 𝑷$ , where $𝑸 \in ℝ^{m \times n}$ is a matrix with orthonormal columns.

The complementary orthogonal projector projects a vector onto the left null space, $N (𝑸^{T})$

Orthogonal projectors and linear systems

Consider the linear system $𝑨 𝒙 = 𝒃$ with $𝑨 \in ℝ^{m \times n}$ , $𝒙 \in ℝ^{n}$ , $𝒃 \in ℝ^{m}$ . Orthogonal projectors and knowledge of the four fundamental matrix subspaces allows us to succintly express whether there exist no solutions, a single solution of an infinite number of solutions:
- Consider the factorization $𝑸 𝑹 = 𝑨$ , the orthogonal projector $𝑷 = 𝑸 𝑸^{T}$ , and the complementary orthogonal projector $𝑰 - 𝑷$
- If $|| (𝑰 - 𝑷) 𝒃 || \neq 0$ , then $𝒃$ has a component outside the column space of $𝑨$ , and $𝑨 𝒙 = 𝒃$ has no solution
- If $|| (𝑰 - 𝑷) 𝒃 || = 0$ , then $𝒃 \in C (𝑸) = C (𝑨)$ and the system has at least one solution
- If $N (𝑨) = {𝟎}$ (null space only contains the zero vector, i.e., null space of dimension 0) the system has a unique solution
- If $\dim N (𝑨) = n - r > 0$ , then a vector $𝒚 \in N (𝑨)$ in the null space is written as
  $𝒚 = c_{1} 𝒛_{1} + \dots + c_{n - r} 𝒛_{n - r}$
  and if $𝒙$ is a solution of $𝑨 𝒙 = 𝒃$ , so is $𝒙 + 𝒚$ , since
  $𝑨 (𝒙 + 𝒚) = 𝑨 𝒙 + c_{1} 𝑨 𝒛_{1} + \dots + c_{n - r} 𝑨 𝒛_{n - r} = 𝒃 + 𝟎 + \dots + 𝟎 = 𝒃$
  The linear system has an $(n - r)$ -parameter family of solutions

Least squares: linear regression calculus approach

In many scientific fields the problem of determining the straight line $y (x) = c_{0} + c_{1} x$ , that best approximate data $𝒟 = {(x_{i}, y_{i}), i = 1, \dots, m}$ arises. The problem is to find the coefficients $c_{0}, c_{1}$ , and this is referred to as the linear regression problem.
The calculus approach: Form sum of squared differences between $y (x_{i})$ and $y_{i}$
$S (c_{0}, c_{1}) = \sum_{i = 1}^{m} {(y (x_{i}) - y_{i})}^{2} = \sum_{i = 1}^{m} {(c_{0} + c_{1} x_{i} - y_{i})}^{2}$
and seek $(c_{0}, c_{1})$ that minimize $S (c_{0}, c_{1})$ by solving the equations
$\frac{\partial S}{\partial c_{0}} = 0 \Rightarrow 2 \sum_{i = 1}^{m} (c_{0} + c_{1} x_{i} - y_{i}) = 0 \Leftrightarrow m c_{0} + (\sum_{i = 1}^{m} x_{i}) c_{1} = \sum_{i = 1}^{m} y_{i}$ $\frac{\partial S}{\partial c_{1}} = 0 \Rightarrow 2 \sum_{i = 1}^{m} (c_{0} + c_{1} x_{i} - y_{i}) x_{i} = 0 \Leftrightarrow (\sum_{i = 1}^{m} x_{i}) c_{0} + (\sum_{i = 1}^{m} x_{i}^{2}) c_{1} = \sum_{i = 1}^{m} x_{i} y_{i}$

Geometry of linear regression

Form a vector of errors with components $e_{i} = y (x_{i}) - x_{i}$ . Recognize that $y (x_{i})$ is a linear combination of $1$ and $x_{i}$ with coefficients $a_{0}, a_{1}$ , or in vector form
$𝒆 = (\begin{array}{cc} 1 & x_{1} \\ ⋮ & ⋮ \\ 1 & x_{m} \end{array}) (\begin{array}{c} c_{0} \\ c_{1} \end{array}) - 𝒚 = (\begin{array}{cc} 𝟏 & 𝒙 \end{array}) 𝒄 - 𝒚 = 𝑨 𝒄 - 𝒚$
The norm of the error vector $|| 𝒆 ||$ is smallest when $𝑨 𝒄$ is as close as possible to $𝒚$ . Since $𝑨 𝒄$ is within the column space of $C (𝑨)$ , $𝑨 𝒄 \in C (𝑨)$ , the required condition is for $𝒆$ to be orthogonal to the column space
$𝒆 ⊥ C (𝑨) \Rightarrow 𝑨^{T} 𝒆 = (\begin{array}{c} 𝟏^{T} \\ 𝒙^{T} \end{array}) 𝒆 = (\begin{array}{c} 𝟏^{T} 𝒆 \\ 𝒙^{T} 𝒆 \end{array}) = (\begin{array}{c} 0 \\ 0 \end{array}) = 𝟎$ $𝑨^{T} 𝒆 = 𝟎 \Leftrightarrow 𝑨^{T} (𝑨 𝒄 - 𝒚) = 0 \Leftrightarrow (𝑨^{T} 𝑨) 𝒄 = 𝑨^{T} 𝒚$