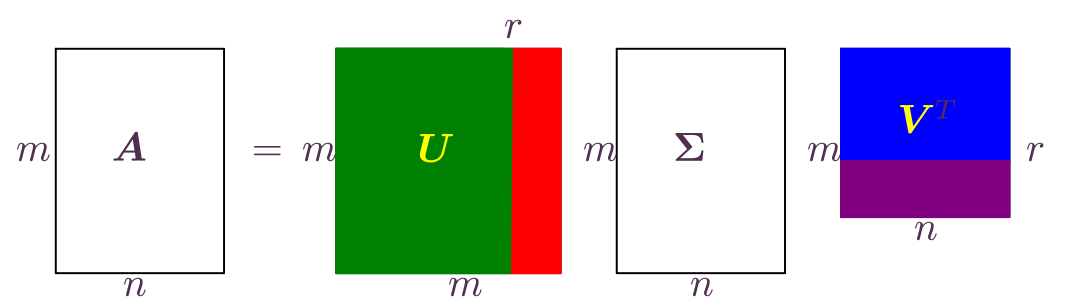MATH347DS L08: Eigenvalue concepts, Singular value decomposition, model reduction

Overview

• Matrix form of eigenvalue problem and applications

• Eigenspaces

• The singular value decomposition (SVD)

• Another essential diagram: SVD finds orthonormal spaces for $C\left(𝑨\right),N\left({𝑨}^T\right),C\left({𝑨}^T\right),N\left(𝑨\right)$

Matrix form of eigenvalue problem

• For $𝑨\in {ℝ}^{m\times m}$, the eigenvalue problem $𝑨𝒙=\lambda 𝒙$ ($𝒙\ne 𝟎$) can be written in matrix form as

  ${\displaystyle 𝑨𝑿=𝑿𝚲,𝑿=\left(\begin{array}{ccc}{𝒙}_1& \dots & {𝒙}_m\end{array}\right)\mathrm{eigenvector},𝚲=\mathrm{diag}({\lambda }_1,\dots ,{\lambda }_m)\mathrm{eigenvalue}\mathrm{matrices}}$

• If the column vectors of $𝑿$ are linearly independent, then $𝑿$ is invertible and $𝑨$ can be represented as

  ${\displaystyle 𝑨=𝑿𝚲{𝑿}^{-1}}$

• The above form can also be used to reduce $𝑨$ to diagonal form

  ${\displaystyle 𝚲={𝑿}^{-1}𝑨𝑿}$

• Link to determinants: “determinant of product = product of determinants”

  ${\displaystyle \det (𝑨𝑿)=\det (𝑿𝚲)\Rightarrow \det \left(𝑨\right)=\det \left(𝚲\right)(\mathrm{for}\det \left(𝑿\right)\ne 0)}$

Eigendecomposition applications: solving ODE systems, matrix iteration

• Diagonal forms are useful in solving linear ODE systems

  ${\displaystyle {𝒚}^{\text{'}}=𝑨𝒚\iff \left({𝑿}^{-1}𝒚\right)=𝚲\left({𝑿}^{-1}𝒚\right)}$

• Also useful in repeatedly applying $𝑨$

  ${\displaystyle {𝒖}_k={𝑨}^k{𝒖}_0=𝑨𝑨\dots 𝑨{𝒖}_0=(𝑿𝚲{𝑿}^{-1})(𝑿𝚲{𝑿}^{-1})\dots (𝑿𝚲{𝑿}^{-1}){𝒖}_0=𝑿{𝚲}^k{𝑿}^{-1}{𝒖}_0}$

When does the eigenmatrix $𝑿$ have independent column vectors?

• For eigenvalue ${\lambda }_i$ of $𝑨\in {ℝ}^{m\times m}$, $E_i=N(𝑨-{\lambda }_i𝑰)$ is the associated eigenspace

• $m_i=\dim E_i$ is the geometric multiplicity of eigenvalue ${\lambda }_i$

• Assume $𝑨\in {ℝ}^{m\times m}$ has $N$ distinct eigenvalues, write the characteristic polynomial as

  ${\displaystyle p\left(\lambda \right)={(\lambda -{\lambda }_1)}^{n_1}\cdot {(\lambda -{\lambda }_2)}^{n_2}\cdot \dots \cdot {(\lambda -{\lambda }_N)}^{n_N},}$

  where $n_i$ is the algebraic multiplicity of eigenvalue ${\lambda }_i$

• If for some $i$, $m_i<n_i$, the matrix $𝑨\in {ℝ}^{m\times m}$ is defective, and $𝑿$ has dependent columns

• If for all $i$, $m_i=n_i$, then $𝑿$ has independent columns, and $𝑨$ is diagonalizable.

Eigenproblem computations: characteristic polynomial

• Octave/Matlab procedures to find characteristic polynomial

  • poly(A) function returns the coefficients

  • roots(p) function computes roots of the polynomial

octave> 

A=[5 -4 2; 5 -4 1; -2 2 -3]; disp(A);

octave> 

p=poly(A); disp(p);

octave> 

r=roots(p); disp(r');

octave> 

octave> 

null(A-eye(3))'

Orthogonal (Unitary) diagonalization

Definition. A matrix is unitarily diagonalizable if it admits an complete, orthonormal set of eigenvectors.

Definition. A matrix $𝑨\in {ℝ}^{m\times m}$ is normal if ${𝑨}^T𝑨=𝑨{𝑨}^T$, or if $𝑨\in {ℂ}^{m\times m}$, ${𝑨}^{\ast }𝑨=𝑨{𝑨}^{\ast }$.

• Some unitarily diagonalizable matrices:

  • orthogonal matrices $𝑼$, $𝑼{𝑼}^T=𝑰$ are unitarily diagonalizable

  • symmetric matrices $𝑺$, $𝑺={𝑺}^T$ are unitarily diagonalizable

  • skew-symmetric matrices $𝒁$, $𝒁=-{𝒁}^T$ are unitarily diagonalizable

  • normal matrices are unitarily diagonalizable

Singular value decomposition

• Singular value decomposition (SVD), for any $𝑨\in {ℝ}^{m\times n}$, $𝑨=𝑼𝚺{𝑽}^T$, with $𝑼\in {ℝ}^{m\times m}$, $𝑽\in {ℝ}^{n\times n}$ orthogonal, $𝚺\in {ℝ}_{+}^{m\times n}$ diagonal

• The SVD is determined by eigendecomposition of $A^{T}A$, and $A{A}^T$

  • $A^{T}A={(U\Sigma V^T)}^T(U\Sigma V^T)=V({\Sigma }^T\Sigma )V^T$, an eigendecomposition of $A^{T}A$. The columns of $V$ are eigenvectors of $A^{T}A$ and called right singular vectors of $A$

  • $A{A}^T=(U\Sigma V^T){(U{\Sigma }^T{V}^T)}^T=U\left(\Sigma {\Sigma }^T\right)U^T$, an eigendecomposition of $A^{T}A$. The columns of $U$ are eigenvectors of $A{A}^T$ and called left singular vectors of $A$

  • The matrix $\Sigma$ has form

    ${\displaystyle \Sigma =\left(\begin{array}{cccccc}{\sigma }_1& & & & & \\ & {\sigma }_2& & & & \\ & & \ddots & & & \\ & & & {\sigma }_r& & \\ & & & & 0& \\ & & & & & \ddots \end{array}\right)\in {ℝ}_{+}^{m.\times n.}}$

    and ${\sigma }_i$ are the singular values of $A$.

The SVD diagram

• The SVD of $𝑨\in {ℝ}^{m\times n}$ reveals: $\mathrm{rank}\left(𝑨\right)$, bases for $C\left(𝑨\right),N\left({𝑨}^T\right),C\left({𝑨}^T\right),N\left(𝑨\right)$

Figure 1. The SVD diagram

Data compression using the SVD

• Rewrite SVD as a sum of rank-one updates ${𝒖}_i{𝒗}_i^T$, with ${\sigma }_1⩾{\sigma }_2⩾\dots ⩾{\sigma }_r>0$

  ${\displaystyle 𝑨=𝑼𝚺{𝑽}^T=\left(\begin{array}{ccc}{𝒖}_1& \dots & {𝒖}_m\end{array}\right)\left(\begin{array}{ccccc}{\sigma }_1& & & & \\ & \ddots & & & \\ & & {\sigma }_r& & \\ & & & 0& \\ & & & & \ddots \end{array}\right)\left(\begin{array}{c}{𝒗}_1^T\\ ⋮\\ {𝒗}_n^T\end{array}\right)=\sum _{i=1}^r{\sigma }_i{𝒖}_i{𝒗}_i^T}$

• A reduced representation can be obtained by using fewer terms in the sum

  ${\displaystyle 𝑨\cong \sum _{i=1}^s{\sigma }_i{𝒖}_i{𝒗}_i,s<r}$