1.MATH347 Homework 0

1.1.Background

This homework is meant to familiarize yourself with basic operations within TeXmacs, a public-domain scientific editing platform. The TeXmacs website provides several tutorials. The key features of TeXmacs that motivate adoption of the platform for this course are:

• Simple, efficient editing of mathematical content. The editor has a default text mode, and also a mathematics mode triggered by inserting an equation from the menu using Insert->Mathematics->(formula type), or the keyboard through key-strokes $, or Alt-Shift-$. Here is an example: the solution of the linear system $𝑨𝒙=𝒃$ with a symmetric matrix, ${𝑨}^T=𝑨$, can be found by gradient descent

  ${\displaystyle \varphi \left(𝒙\right)=\frac{1}{2}{𝒙}^T𝑨𝒙-{𝒃}^T𝒙,{𝒙}^{(k+1)}={𝒙}^{\left(k\right)}-\lambda \nabla \varphi \left({𝒙}^{\left(k\right)}\right).}$ ${\displaystyle \varphi \left(𝒙\right)=\frac{1}{2}{𝒙}^T𝑨𝒙-{𝒃}^T𝒙}$

• Sessions from other mathematical packages can be inserted directly into a document. Julia is used extensively in this course, and the menu item Insert->Session->Julia leads to creation of space within the document to execute Julia instructions. Define a matrix $𝑨$.

  ∴	A=[1 2 3; -1 0 1; 2 1 -2]

  ${\displaystyle \left[\begin{array}{ccc}1& 2& 3\\ -1& 0& 1\\ 2& 1& -2\end{array}\right]}$

  (1)

  Extend the Julia environment by adding a package to compute row echelon forms. This need be done only once.

  ∴	import Pkg; Pkg.add("RowEchelon");

  Resolving package versions…

  No Changes to ‘~/.julia/environments/v1.9/Project.toml‘

  No Changes to ‘~/.julia/environments/v1.9/Manifest.toml‘

  Load the RowEchelon package into the current session and invoke the rref function.

  ∴	using RowEchelon

  ∴

  rref(A)

  ${\displaystyle \left[\begin{array}{ccc}1.0& 0.0& 0.0\\ 0.0& 1.0& 0.0\\ 0.0& 0.0& 1.0\end{array}\right]}$

  (2)

  Compute the inverse of the matrix $𝑨$.

  ∴

  inv(A)

  ${\displaystyle \left[\begin{array}{ccc}0.25000000000000006& -1.7500000000000002& -0.5000000000000002\\ -1.1102230246251565e-16& 2.0000000000000004& 1.0000000000000002\\ 0.25000000000000006& -0.7500000000000002& -0.5000000000000001\end{array}\right]}$

  (3)

  ∴

• Documents can readily be converted to other formats: PDF, LaTeX, HTML. All course documents, including the website are produced with TeXmacs.

1.2.Theoretical questions

1.2.1.Text editing in TeXmacs

Problem

Write an itemized list of ingredients in your favorite dessert recipe. (Menu->Insert->Itemize)

Answer

1.2.2.Inline mathematics

Problem

The fundamental theorem of calculus states ${\int }_a^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)$ for $F^{\text{'}}\left(x\right)=f\left(x\right)$. Apply this result for $a=0$, $b=\pi$, $f\left(x\right)=\sin x$, $F\left(x\right)=-\cos x$. Write your answer inline.

Answer

1.2.3.Displayed mathematics

Problem

A matrix is a row of column vectors, $𝑨=\left[\begin{array}{llll}{𝒂}_1& {𝒂}_2& \dots & {𝒂}_n\end{array}\right]\in {ℝ}^{m\times n}$, which can be expressed in terms of vector components as

${\displaystyle 𝑨=\left[\begin{array}{llll}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \dots & a_{\mathrm{mn}}\end{array}\right].}$

Look up the definition of a Hilbert matrix $𝑯$ and write in the above forms, both as a row of column vectors, and as components.

Answer

1.2.4.Julia session - working with numbers

Problem

Insert a Julia session and produce a table of the squares and cubes of the first ten natural numbers.

Answer

1.2.5.Julia session - working with column vectors

Problem

Insert a Julia session and define the vectors

${\displaystyle 𝒖=\left[\begin{array}{l}1\\ 2\\ 3\end{array}\right],𝒗=\left[\begin{array}{l}-1\\ 0\\ 1\end{array}\right],𝒘=\left[\begin{array}{l}0\\ -1\\ 0\end{array}\right].}$

Answer

1.2.6.Julia session - working with row vectors

Problem

Insert a Julia session and define the vectors

${\displaystyle 𝒂=\left[\begin{array}{lll}1& 2& 3\end{array}\right],𝒃=\left[\begin{array}{lll}-1& 0& 1\end{array}\right],𝒄=\left[\begin{array}{lll}0& -1& 0\end{array}\right].}$

Answer

1.2.7.Julia session - assembling column vectors into a matrix

Problem

Insert a Julia session and define the matrix $𝑿=\left[\begin{array}{lll}𝒖& 𝒗& 𝒘\end{array}\right].$

Answer

1.2.8.Julia session - assembling row vectors into a matrix

Problem

Insert a Julia session and define the matrix

${\displaystyle 𝒀=\left[\begin{array}{l}𝒂\\ 𝒃\\ 3𝒄\end{array}\right]}$

Answer

1.2.9.Julia session - componentwise definition of a matrix

Problem

Insert a Julia session and display the Hilbert matrix $𝑯\in {ℝ}^{4\times 4}$.

Answer

1.2.10.Julia session - constructing plots

Problem

Insert a Julia session to plot the function $f\left(x\right)=\sin \left(\cos \left(x\right)\right)+\cos \left(\sin \left(x\right)\right)$.

Answer

1.3.Data Science Application

Carry out linear regression, i.e., fitting a line to data.

1.3.1.Generate synthetic data

Problem

The following generates data by random perturbation of points on a line $y=c_0+c_{1}x$.

∴	m=20; x=(0:m-1)/m; c0=-1; c1=1; yex=c0 .+ c1*x;

∴	y=yex .+ 0.1*(rand(m,1) .- 0.5);

∴	clf(); plot(x,yex,"k",x,y,"r.");

∴	cd(homedir()*"/courses/MATH347DS/homework/hw00");

∴	savefig("H00Fig01.eps");

∴

Repeat for different values of $m,c_0,c_1$.

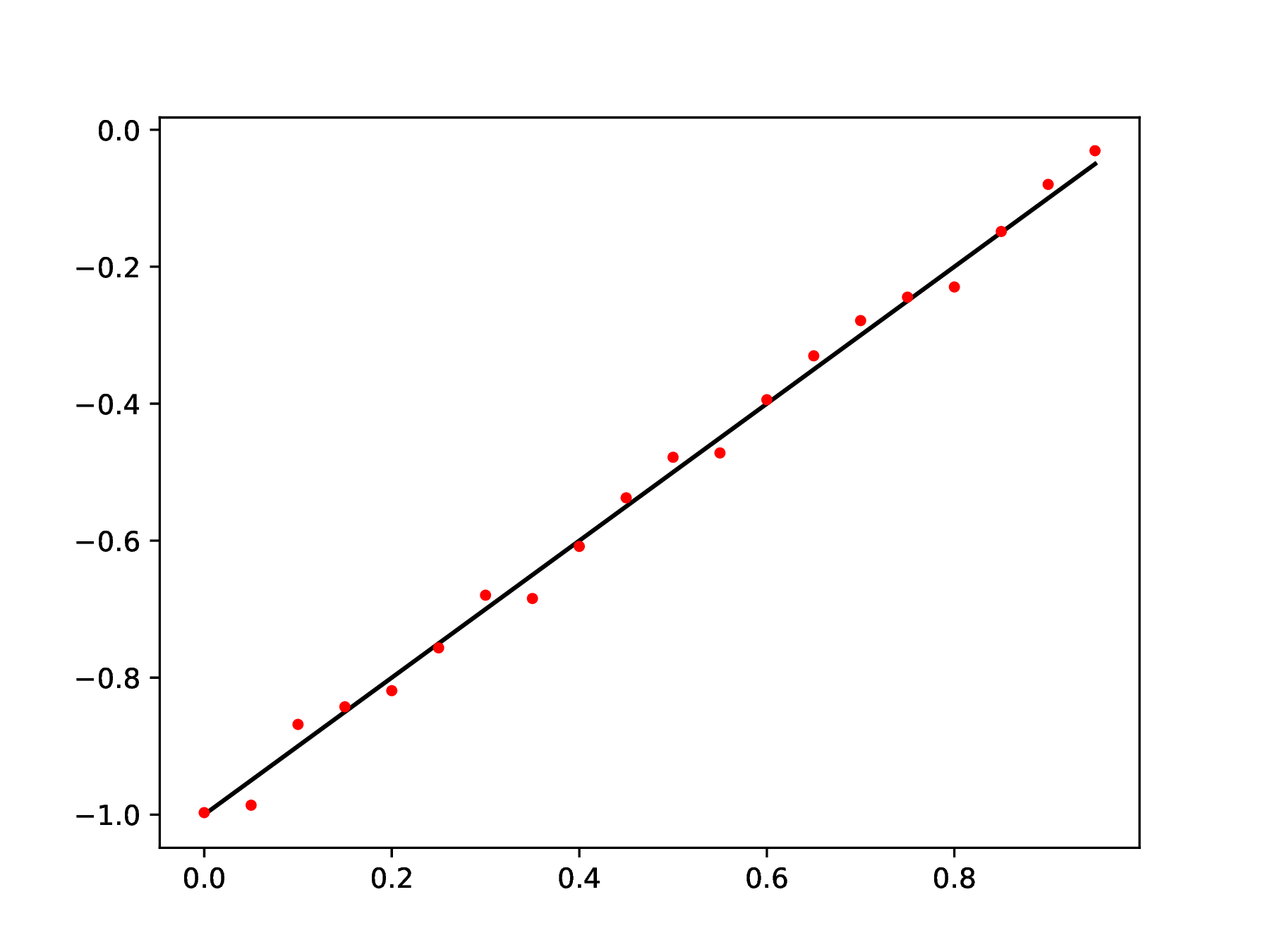Figure 1. Perturbation of points on a line.

Answer

1.3.2.Form the normal system

Problem

Define matrices $𝑿=\left[\begin{array}{ll}𝟏& 𝒙\end{array}\right]$, $𝑵={𝑿}^T𝑿$, and vector $𝒃={𝑿}^T𝒚$

Answer

1.3.3.Solve the least square problem

Problem

Solve the system $𝑵𝒄=𝒃$ by use of the Octave backslash operator c=N\b. Display the coefficient vector $𝒄$, and compare to the values you chose in Question 3.1. Also compute $\stackrel{\sim }{𝒚}=𝑿𝒄$, using ytilde as a notation.

Answer

1.3.4.Plot the result

Problem

Plot the original line, perturbed points and linear regression of the perturbed points.

Answer

Submission instructions. Save your work, and also export to PDF (menu File->Export->Pdf). In Canvas submit the files:

• hw00.tm

• hw00.pdf