1.MATH347 Homework 1

1.1.Background

This homework is meant as a tutorial on matrix computations, in particular:

• vector addition and scaling;

• vector norms;

• inner products;

• matrix-vector products;

• linear mapping matrices;

• linear mapping composition matrix-matrix products.

1.2.Theoretical questions

1.2.1.Vector addition and scaling

Problem

Consider $n$ gray-scale images of size $p\times q$ pixels, where the brightness value of pixel at position $(i,j)$, $1⩽i⩽p$, $1⩽j⩽q$ is $0⩽b_{ij}^{\left(l\right)}<2^{R+1}$, $1⩽l⩽n$, $R\in {\mathbb{N}}_{+}$.

1. Represent the images as column vectors ${𝒂}_k$ of a matrix $𝑨=\left[\begin{array}{lll}{𝒂}_1& \cdots & {𝒂}_n\end{array}\right]=\left[a_{kl}\right]$. What is the matrix size?

2. Construct a composite image $𝒃$ obtained by taking fractions $0⩽x_l⩽1$ of image $l$, $1⩽l⩽n$, $x_l\in [0,1]$.

Answer

1.2.2.Norms in $E_m$

Problem

Verify whether for $a_1,a_2>0$, $f:{ℝ}^2\to {ℝ}_{+}$ defined by

${\displaystyle f\left(𝒙\right)=a_1{x}_1^2+a_2{x}_2^2,}$

is a norm in $E_2$.

Answer

1.2.3.Norms in $E_m$

Problem

Verify whether for $a_1,a_2>0$, $f:{ℝ}^2\to {ℝ}_{+}$ defined by

${\displaystyle f\left(𝒙\right)=a_1{x}_1^2-a_2{x}_2^2}$

is a norm in $E_2$.

Answer

1.2.4.Inner product in $E_m$

Problem

Verify whether for $a_1>0,a_2>0$, $s:{ℝ}^2\times {ℝ}^2\to ℝ$ defined by

${\displaystyle s(𝒙,𝒚)=a_1{x}_1{y}_1+a_2{x}_2{y}_2,}$

is a scalar product in $E_2$.

Answer

1.2.5.Inner product in $E_m$

Problem

Verify whether for $a_1,a_2>0$, $s:{ℝ}^2\times {ℝ}^2\to ℝ$ defined by

${\displaystyle s(𝒙,𝒚)=a_1{x}_1{y}_1-a_2{x}_2{y}_2,}$

is a scalar product in $E_2$.

Answer

1.2.6.Matrix-matrix products

Problem

Verify that the “row-over-columns” matrix multiplication rule is equivalent to columns of matrix-vector multiplications, i.e., for $𝑨\in {ℝ}^{m\times n}$, $𝑩\in {ℝ}^{n\times p}$, $𝑪\in {ℝ}^{m\times p}$

${\displaystyle 𝑨𝑩=\left[\begin{array}{llll}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \dots & a_{\mathrm{mn}}\end{array}\right]\left[\begin{array}{llll}{b}_{11}& b_{12}& \dots & b_{1p}\\ b_{21}& b_{22}& \dots & b_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ b_{n1}& b_{n2}& \dots & b_{np}\end{array}\right]=𝑨\left[\begin{array}{llll}{𝒃}_1& {𝒃}_2& \dots & {𝒃}_p\end{array}\right]=\left[\begin{array}{llll}𝑨{𝒃}_1& 𝑨{𝒃}_2& \dots & 𝑨{𝒃}_p\end{array}\right]}$

Answer

1.2.7.

Linear mapping representation

Problem

Determine the matrix $𝑪$ of the linear mapping $𝒉:{ℝ}^2\to {ℝ}^2$ representing rotation of a vector by angle $\theta$ followed by reflection across the $x_2$-axis. Let $𝑨,𝑩$ denote the matrices of the mappings $𝒇,𝒈$ corresponding to: (1) reflection by angle $\theta$; (2) reflection across the $x_2$-axis. Verify that $𝒉=𝒈\circ 𝒇$ corresponds to $𝑪=𝑩𝑨$. Does $𝑪=𝑨𝑩$?

Answer

1.2.8.

Linear mapping composition

Problem

Construct the rotation matrices $𝑨,𝑩,𝑪$ for rotation by angles $\theta ,\phi ,\theta +\phi$. Verify $𝑪=𝑩𝑨$, and the trigonometric identities for sine and cosine of sums of angles. Does $𝑪=𝑨𝑩$? Compare your answer to previous case.

Answer

1.2.9.

Block matrix operations

Problem

Identify repeated blocks in the matrices $𝑨,𝑩$ and carry out the mutiplication in Julia: (1) componentwise; (2) by blocks. Compare the two results.

${\displaystyle 𝑪=𝑨{𝑩}^T=\left[\begin{array}{llll}2& 1& 0& 3\\ 3& 2& 3& 0\\ 0& 3& 2& 1\\ 3& 0& 3& 2\end{array}\right]{\left[\begin{array}{llll}2& 3& 1& 1\\ 1& 2& 2& 1\\ 1& 2& 2& 3\\ 1& 1& 1& 2\end{array}\right]}^T}$

Answer

1.2.10.

Block matrix operations

Problem

Carry out the following block matrix multiplication

${\displaystyle 𝑨=𝑼𝚺{𝑽}^T=\left[\begin{array}{llll}{𝒖}_1& {𝒖}_2& \dots & {𝒖}_m\end{array}\right]\left[\begin{array}{llll}{\sigma }_1& 0& \cdots & 0\\ 0& {\sigma }_2& & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & {\sigma }_n\\ 0& 0& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & 0\end{array}\right]{\left[\begin{array}{llll}{𝒗}_1& {𝒗}_2& \dots & {𝒗}_n\end{array}\right]}^T.}$

Answer

1.3.Linear functionals and mappings in analysis of EEG data

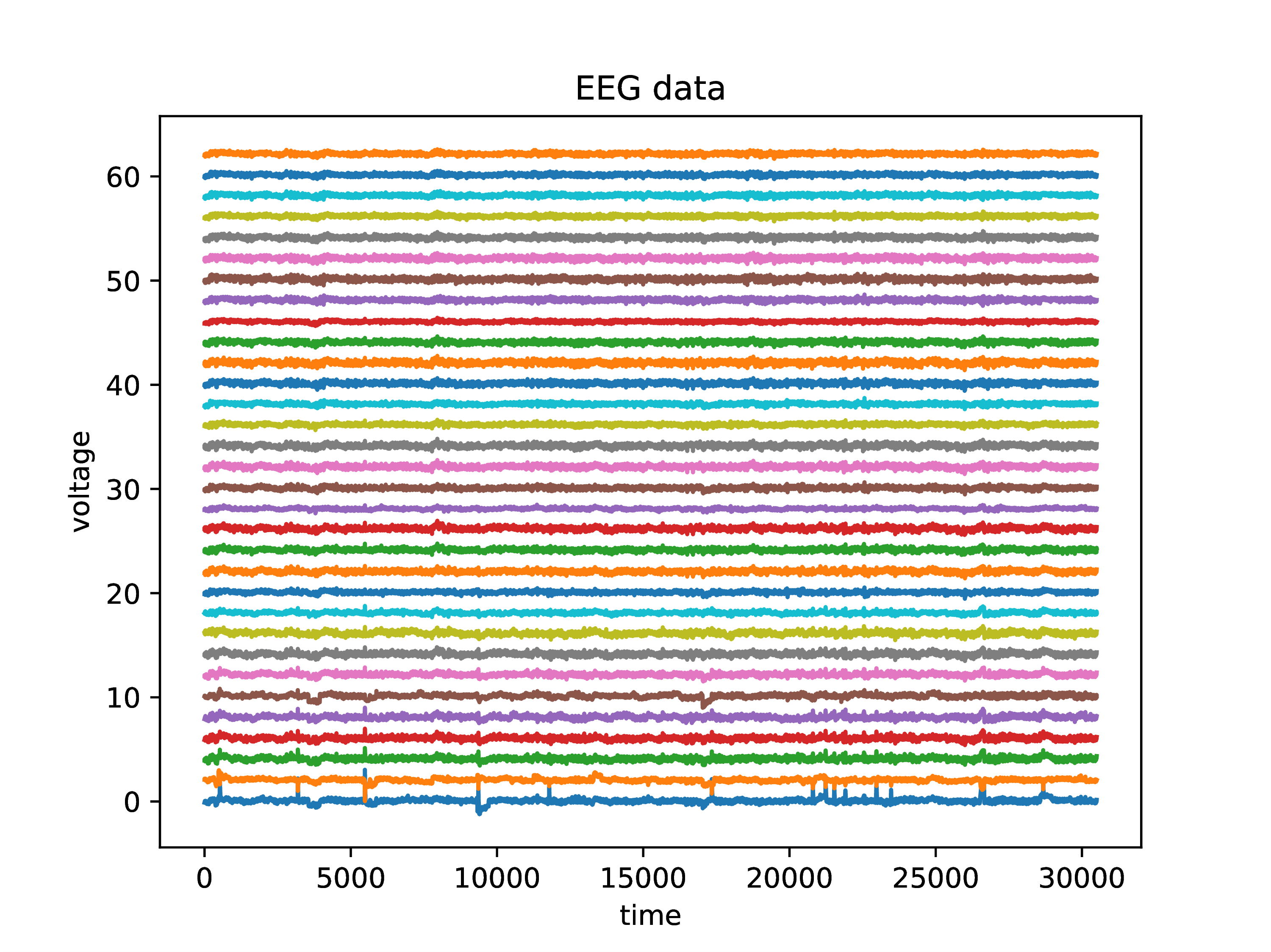
Electroencephalograms (EEGs) are recordings of the electric potential on cranium skin. Research on brain activity uses EEGs to determine specific activity patterns in the brain. For example, epileptic seizures have a distinctive EEG signature. EEG data can be loaded from the course data directory. As is typically the case in data analysis, an additional package is required to read in the particular data format; in this case the data is given in Matlab .mat format. This need only be done once.

∴ 

import Pkg; Pkg.add("MAT");

∴ 

using MAT

∴ 

DataFileName = homedir()*"/courses/MATH347DS/data/eeg/eeg.mat";

∴ 

DataFile = matopen(DataFileName,"r");

∴ 

dict = read(DataFile,"EEG");

∴ 

data = dict["data"]';

∴ 

m,n=size(data)

∴ 

mx=findmax(data[:,4:28])[1]; mn=findmin(data[:,4:28])[1];

∴ 

d = 2*(data .- mn)/(mx-mn) .- 1;

∴ 

clf();

∴ 

for j=1:n
 plot(d[:,j].+(j-1)*2)
end

∴ 

xlabel("time"); ylabel("voltage"); title("EEG data");

∴ 

cd(homedir()*"/courses/MATH347DS/homework/hw01");

∴ 

savefig("H01Fig01.eps");

∴ 

Figure 1. Electrode voltage time history in EEG

∴ 

clf();

∴ 

for j=1:4
 plot(d[1000:1500,j].+(j-1)*2)
end

∴ 

xlabel("time"); ylabel("voltage"); title("EEG data portion"); grid("on");

∴ 

savefig("H01Fig02.eps");

∴ 

Figure 2. Detail of recordings from first four electrodes.

1.3.1.Functional relationships in the data (functions)

Over some time subinterval, can the data from a sensor be expressed as a function of data from another sensor?

1.3.2.Data magnitude (norm)

Partition sensor data into time subintervals. Over each subinterval, evaluate the $p$-norm of centered data, for $p=1,2,3$, $p\to \infty$. Plot the $p$-norms over the entire time history.

1.3.3.Orthogonality of sensor data (inner product)

Over some time interval, determine the angle between sensor data. Is sensor data orthogonal? Plot the angle between sensor data over the entire time history.

1.3.4.Linear relationships in the data (linear mapping)

Can data from a sensor be expressed as a linear combination of other sensors?