1.MATH347 Homework 3

1.1.Background

This homework investigates consequences of the fundamental theorem of algebra and application of the singular value decomposition.

1.2.Theoretical questions

Consider a linear mapping $𝒇:U\to V$, from vector space $𝒰=(U,ℝ,+,\cdot )$ with basis $\{{𝒖}_1,\dots ,{𝒖}_n\}$, to $𝒱=(V,ℝ,+,\cdot )$, with basis $\{{𝒗}_1,\dots ,{𝒗}_m\}$.

1. Is $\{𝒇\left({𝒖}_1\right),\dots ,𝒇\left({𝒖}_n\right)\}$ a basis for $𝒱$? (1 point)

2. If $\mathrm{nullity}\left(𝒇\right)=0$ must $m=n$? (1 point)

3. If $m=n$ and ${𝒖}_i={𝒗}_i$ for $i=1,\dots ,m$, what is the matrix $𝑨$ representing $𝒇$? (2 points)

4. Determine the singular value decomposition and pseudo-inverse of a matrix $𝑨\in {ℝ}^{1\times n}$ (i.e., a row vector). (2 points)

1.3.Ordered bases for the fundamental spaces and painting motifs

1.3.1.Introduction

The fudamental theorem of linear algebra partitions the domain and codomain of a linear mapping. The singular value decomposition provides orthogonal bases for each of the subspaces arising in the partition. The bases are ordered according to the amplification behavior of the linear mapping, expressed through the norm of successive restrictions of the mapping. This approach is closely aligned with typical problems in data science, and can be used in a variety of scenarios. In this homework linear algebra methods will first be used in a field far removed from the physical sciences: extracting the quirks of painter style from the overall composition of a painting, and applying one artist's style to another artist's composition. This is often-encountered data science problem: distinguishing between small and large scale features of data.

∴ 

mkpath(homedir()*"/courses/MATH347DS/homework/hw03");

∴ 

cd(homedir()*"/courses/MATH347DS/homework/hw03");

∴ 

using Images

∴ 

imFK96=Gray.(load("./paintings/Frida_Kahlo_96.jpg"));

∴ 

AFK96=Real.(imFK96);

∴ 

mx,my=size(AFK96)

∴ 

F=svd(AFK96);

∴ 

norm(AFK96-F.U*Diagonal(F.S)*F.Vt)

∴ 

Load another image, select a portion of the same size as previous image and compute its SVD.

∴ 

imVvG95=Gray.(load("./paintings/Vincent_van_Gogh_95.jpg"));

∴ 

size(imVvG95)

∴ 

AVvG95=Real.(imVvG95)[1:mx,1:my];

∴ 

G=svd(AVvG95);

∴ 

Note that the singular values of the two images decay rapidly

∴ 

clf(); plot(1:my,F.S,".b",1:my,G.S,".r"); xlabel("i"); ylabel(L"$\sigma_i$");

∴ 

savefig("hw03f01.eps");

∴ 

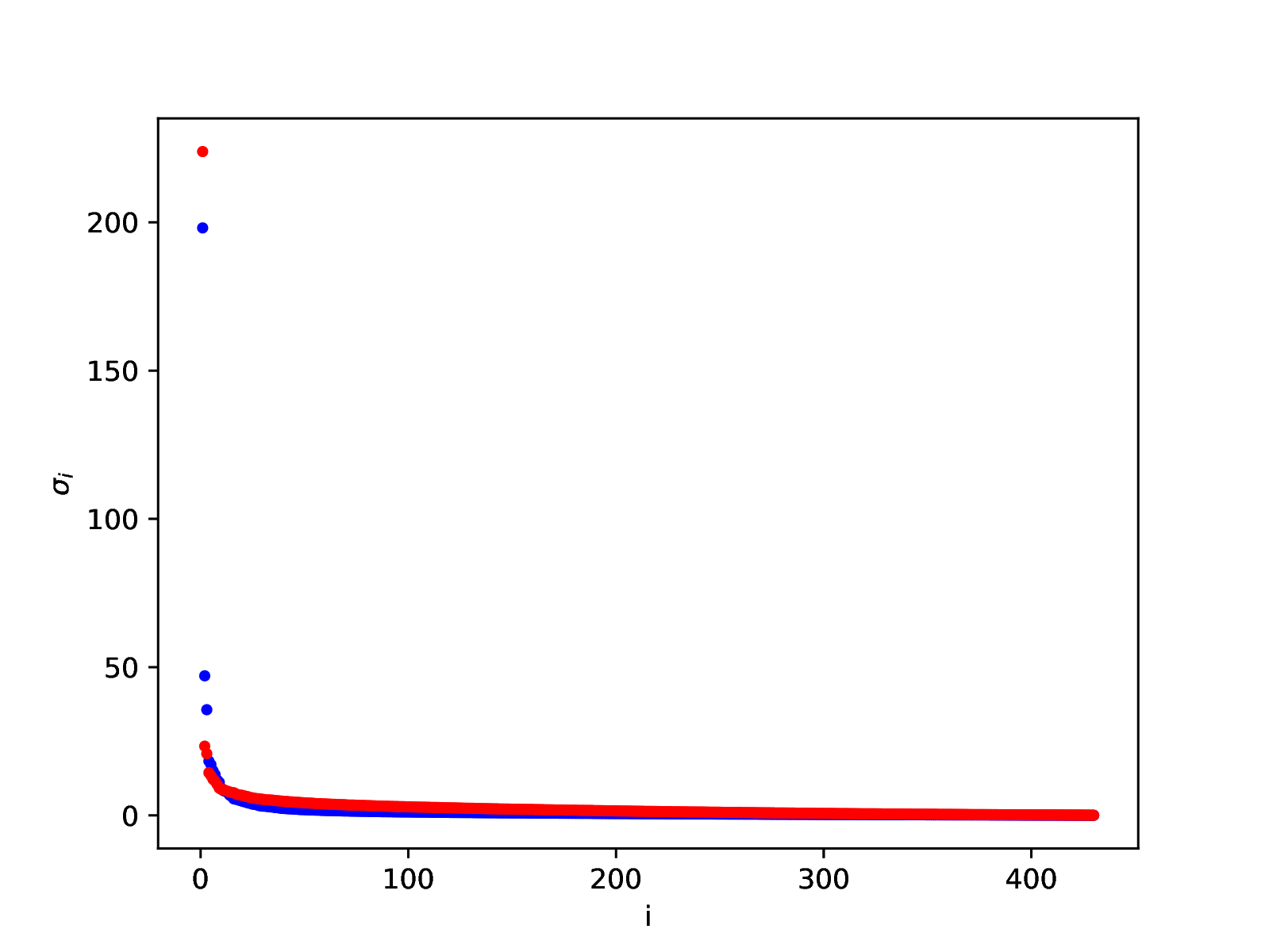Figure 1. Singular values ${\sigma }_i$ of the two images.

Generate a new image by combining the large-scale features of the first image and the small-scale features of the second. Choose the new image to reflect 70% ($x_1=0.3$ of the composition of the first image and 30% ($x_2=0.7$) of the small-scale features of the second. Choose large scale features of the first image to include rank-1 updates from 1 to $k_A$. Choose small scale features of the second image to include rank-1 updates from $k_B$ to $l_B$.

∴ 

x1=0.3; x2=0.7; kA=40; kB=80; lB=120;

∴ 

A1 = F.U[:,1:kA]*Diagonal(F.S[1:kA])*F.Vt[1:kA,:];

∴ 

B1 = G.U[:,kB:lB]*Diagonal(G.S[kB:lB])*G.Vt[kB:lB,:];

∴ 

Anew=x1*A1+x2*B1;

∴ 

figure(1); clf(); imshow(A1,cmap="gray"); savefig("hw03A1.png");

∴ 

figure(2); clf(); imshow(B1,cmap="gray"); savefig("hw03B1.png");

∴ 

figure(3); clf(); imshow(Anew,cmap="gray"); savefig("hw03Anew.png");

∴ 

Figure 2. A new painting (right) reflecting the composition of the Frida Kahlo self portrait (left) with the brush stroke extracted from the Vincent van Gogh self-portrait (middle).

1.3.2.Tasks

Generate 4 different new paintings (3 points each) experimenting with various images as presented above. Comment each result.