MATH347DS

Synopsis. Vectors have been introduced as a mathematical object to represent complicated objects. A framework for working with vectors based upon observations of velocity vectors has been introduced. A procedure for obtaining new vectors from some predetermined set has been formally defined as a linear combination, and the matrix-vector product has been introduced to concisely state this operation. Consideration of multiple linear combinations leads to the definition of matrix-matrix products. Functions that transform input vectors into output vectors have been defined, with those that preserve linear combinations playing a distinguished role, the linear mappings. Matrices also arise in the description of linear mappings. Now that the mathematical framework has been established, a natural question to ask is whether it is complete. Could all questions of interest about linear combinations be answered within this framework. The Fundamental Theorem of Linear Algebra (FTLA) gives an affirmative, but non-constructive answer to this question.

1.Partition of linear mapping domain and codomain

A partition of a set $S$ is a collection of subsets $P = {S_{i} | S_{i} \subset P, S_{i} \neq \emptyset .}$ such that any given element $x \in S$ belongs to only one set in the partition. This is modified when applied to subspaces of a vector space, and a partition of a set of vectors is understood as a collection of subsets such that any vector except $𝟎$ belongs to only one member of the partition.

Linear mappings between vector spaces $𝒇 : U \to V$ can be represented by matrices $𝑨$ with columns that are images of the columns of a basis ${𝒖_{1}, 𝒖_{2}, \dots}$ of $U$

𝑨 = [\begin{array}{ccc} 𝒇 (𝒖_{1}) & 𝒇 (𝒖_{2}) & \dots \end{array}] .

Consider the case of real finite-dimensional domain and co-domain, $𝒇 : ℝ^{n} \to ℝ^{m}$ , in which case $𝑨 \in ℝ^{m \times n}$ ,

𝑨 = [\begin{array}{cccc} 𝒇 (𝒆_{1}) & 𝒇 (𝒆_{2}) & \dots & 𝒇 (𝒆_{n}) \end{array}] = [\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}] .

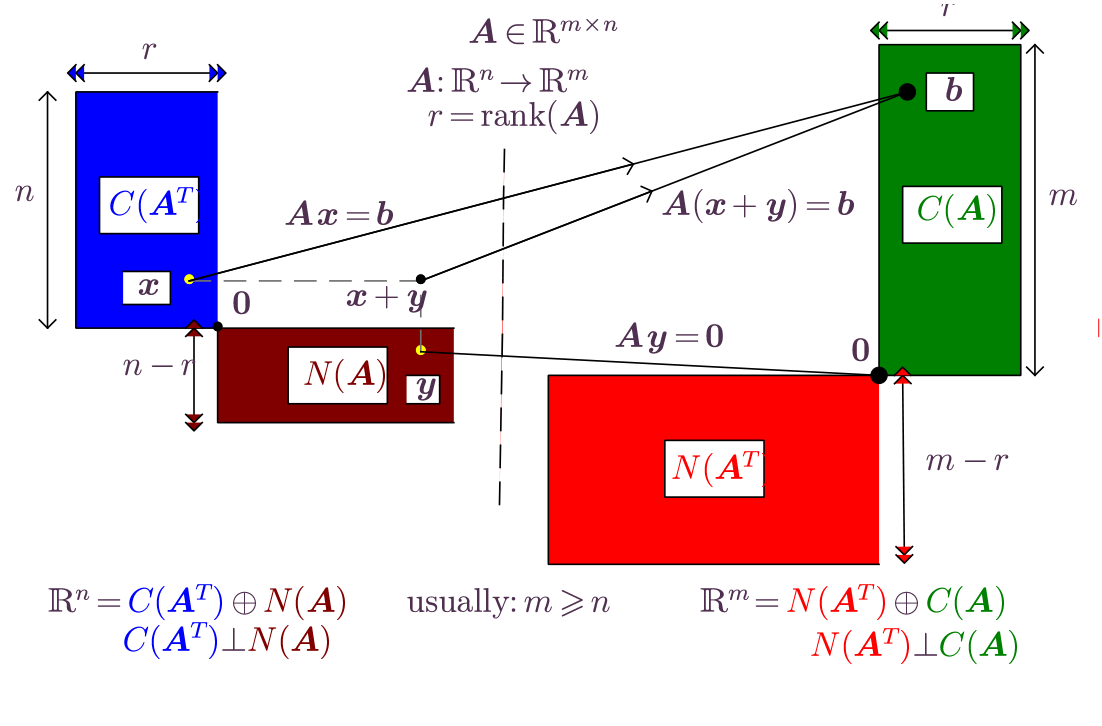
The column space of $𝑨$ is a vector subspace of the codomain, $C (𝑨) \leq ℝ^{m}$ , but according to the definition of dimension if $n < m$ there remain non-zero vectors within the codomain that are outside the range of $𝑨$ ,

n < m \Rightarrow \exists 𝒗 \in ℝ^{m}, 𝒗 \neq 𝟎, 𝒗 \notin C (𝑨) .

All of the non-zero vectors in $N (𝑨^{T})$ , namely the set of vectors orthogonal to all columns in $𝑨$ fall into this category. The above considerations can be stated as

\begin{array}{cccc} C (𝑨) \leq ℝ^{m}, & N (𝑨^{T}) \leq ℝ^{m}, & C (𝑨) ⊥ N (𝑨^{T}) & C (𝑨) + N (𝑨^{T}) \leq ℝ^{m} \end{array} .

The question that arises is whether there remain any non-zero vectors in the codomain that are not part of $C (𝑨)$ or $N (𝑨^{T})$ . The fundamental theorem of linear algebra states that there no such vectors, that $C (𝑨)$ is the orthogonal complement of $N (𝑨^{T})$ , and their direct sum covers the entire codomain $C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ .

Lemma 1. Let $𝒰, 𝒱$ , be subspaces of vector space $𝒲$ . Then $𝒲 = 𝒰 \oplus 𝒱$ if and only if

$𝒲 = 𝒰 + 𝒱$ , and

$𝒰 \cap 𝒱 = {𝟎}$ .

Proof. $𝒲 = 𝒰 \oplus 𝒱 \Rightarrow 𝒲 = 𝒰 + 𝒱$ by definition of direct sum, sum of vector subspaces. To prove that $𝒲 = 𝒰 \oplus 𝒱 \Rightarrow 𝒰 \cap 𝒱 = {𝟎}$ , consider $𝒘 \in 𝒰 \cap 𝒱$ . Since $𝒘 \in 𝒰$ and $𝒘 \in 𝒱$ write

$\begin{array}{llll} 𝒘 = 𝒘 + 𝟎 & (𝒘 \in 𝒰, 𝟎 \in 𝒱), & 𝒘 = 𝟎 + 𝒘 & (𝟎 \in 𝒰, 𝒘 \in 𝒱), \end{array}$

and since expression $𝒘 = 𝒖 + 𝒗$ is unique, it results that $𝒘 = 𝟎$ . Now assume (i),(ii) and establish an unique decomposition. Assume there might be two decompositions of $𝒘 \in 𝒲$ , $𝒘 = 𝒖_{1} + 𝒗_{1}$ , $𝒘 = 𝒖_{2} + 𝒗_{2}$ , with $𝒖_{1}, 𝒖_{2} \in 𝒰$ , $𝒗_{1}, 𝒗_{2} \in 𝒱 .$ Obtain $𝒖_{1} + 𝒗_{1} = 𝒖_{2} + 𝒗_{2}$ , or $𝒙 = 𝒖_{1} - 𝒖_{2} = 𝒗_{2} - 𝒗_{1}$ . Since $𝒙 \in 𝒰$ and $𝒙 \in 𝒱$ it results that $𝒙 = 𝟎$ , and $𝒖_{1} = 𝒖_{2}$ , $𝒗_{1} = 𝒗_{2}$ , i.e., the decomposition is unique. $□$

In the vector space $U + V$ the subspaces $U, V$ are said to be orthogonal complements is $U ⊥ V$ , and $U \cap V = {𝟎}$ . When $U \leq ℝ^{m}$ , the orthogonal complement of $U$ is denoted as $U^{⊥}$ , $U \oplus U^{⊥} = ℝ^{m}$ .

2.The FTLA

Theorem. Given the linear mapping associated with matrix $𝑨 \in ℝ^{m \times n}$ we have:

$C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ , the direct sum of the column space and left null space is the codomain of the mapping

$C (𝑨^{T}) \oplus N (𝑨) = ℝ^{n}$ , the direct sum of the row space and null space is the domain of the mapping

$C (𝑨) ⊥ N (𝑨^{T})$ and $C (𝑨) \cap N (𝑨^{T}) = {𝟎}$ , the column space is orthogonal to the left null space, and they are orthogonal complements of one another,
$\begin{array}{ll} C (𝑨) = N {(𝑨^{T})}^{⊥}, & N (𝑨^{T}) = C {(𝑨)}^{⊥} \end{array} .$

$C (𝑨^{T}) ⊥ N (𝑨)$ and $C (𝑨^{T}) \cap N (𝑨) = {𝟎}$ , the row space is orthogonal to the null space, and they are orthogonal complements of one another,
$\begin{array}{ll} C (𝑨^{T}) = N {(𝑨)}^{⊥}, & N (𝑨) = C {(𝑨^{T})}^{⊥} \end{array} .$

Consideration of equality between sets arises in proving the above theorem. A standard technique to show set equality

A = B

, is by double inclusion,

A \subseteq B \land B \subseteq A \Rightarrow A = B

. This is shown for the statements giving the decomposition of the codomain

ℝ^{m}

. A similar approach can be used to decomposition of

ℝ^{n}

The remainder of the FTLA is established by considering

𝑩 = 𝑨^{T}

, e.g., since it has been established in (v) that

C (𝑩) \oplus N (𝑨^{T}) = ℝ^{n}

, replacing

𝑩 = 𝑨^{T}

yields

C (𝑨^{T}) \oplus N (𝑨) = ℝ^{n}

, etc.

3.The main problems of linear algebra

The FTLA asserts that the framework of linear algebra is complete, we can answer any question about linear combinations. What are the types of questions that are asked? These are known as the main problems of linear algebra.