MATH347DS

MATH347DS L02: Linear Mappings

Overview

Functions
Measurements: norm, inner product, angles
Linear mappings
Linear mapping representation
Linear mapping composition
Linear mapping examples
Matrix product properties
Block matrix operations

Functions

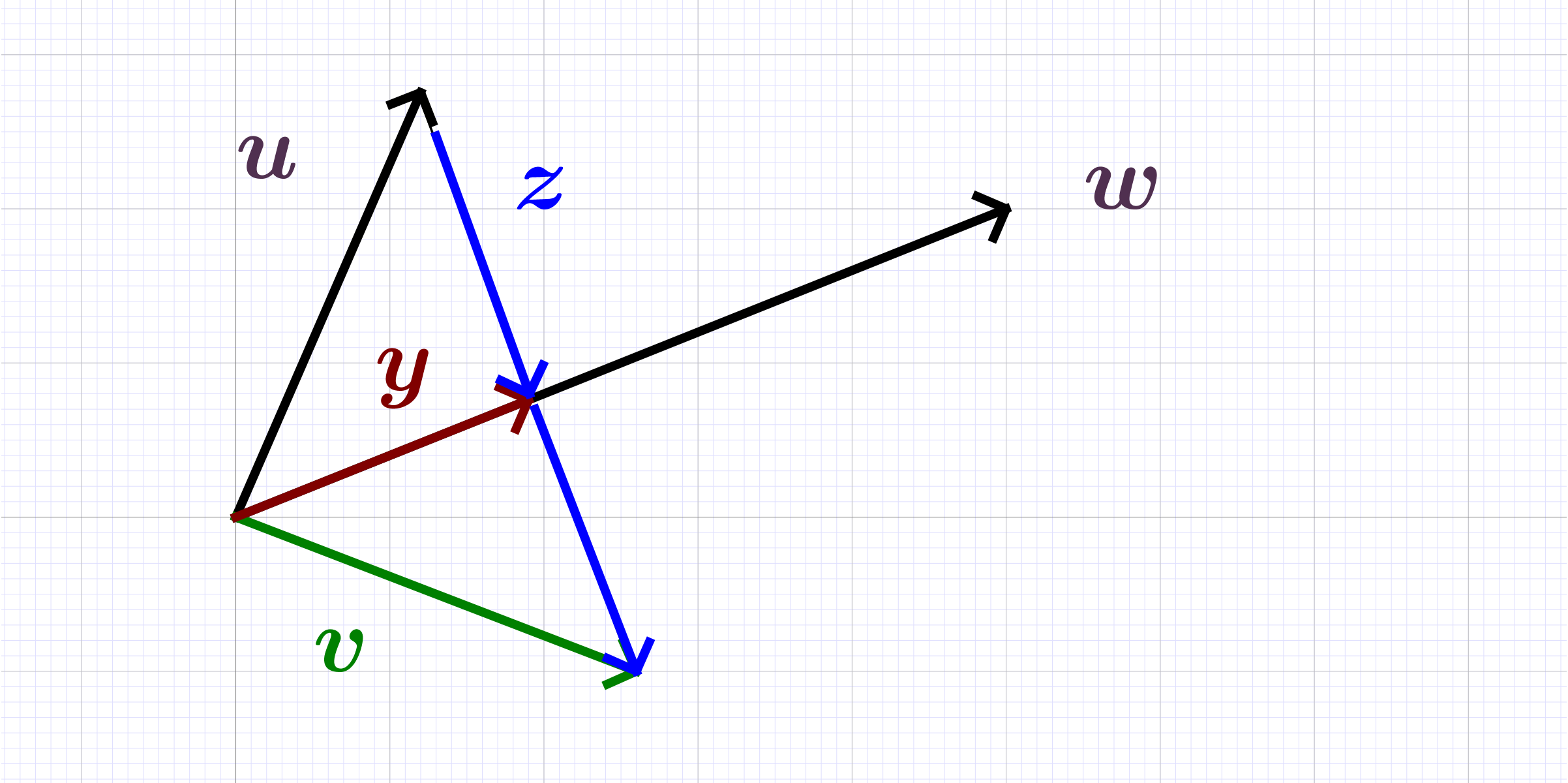
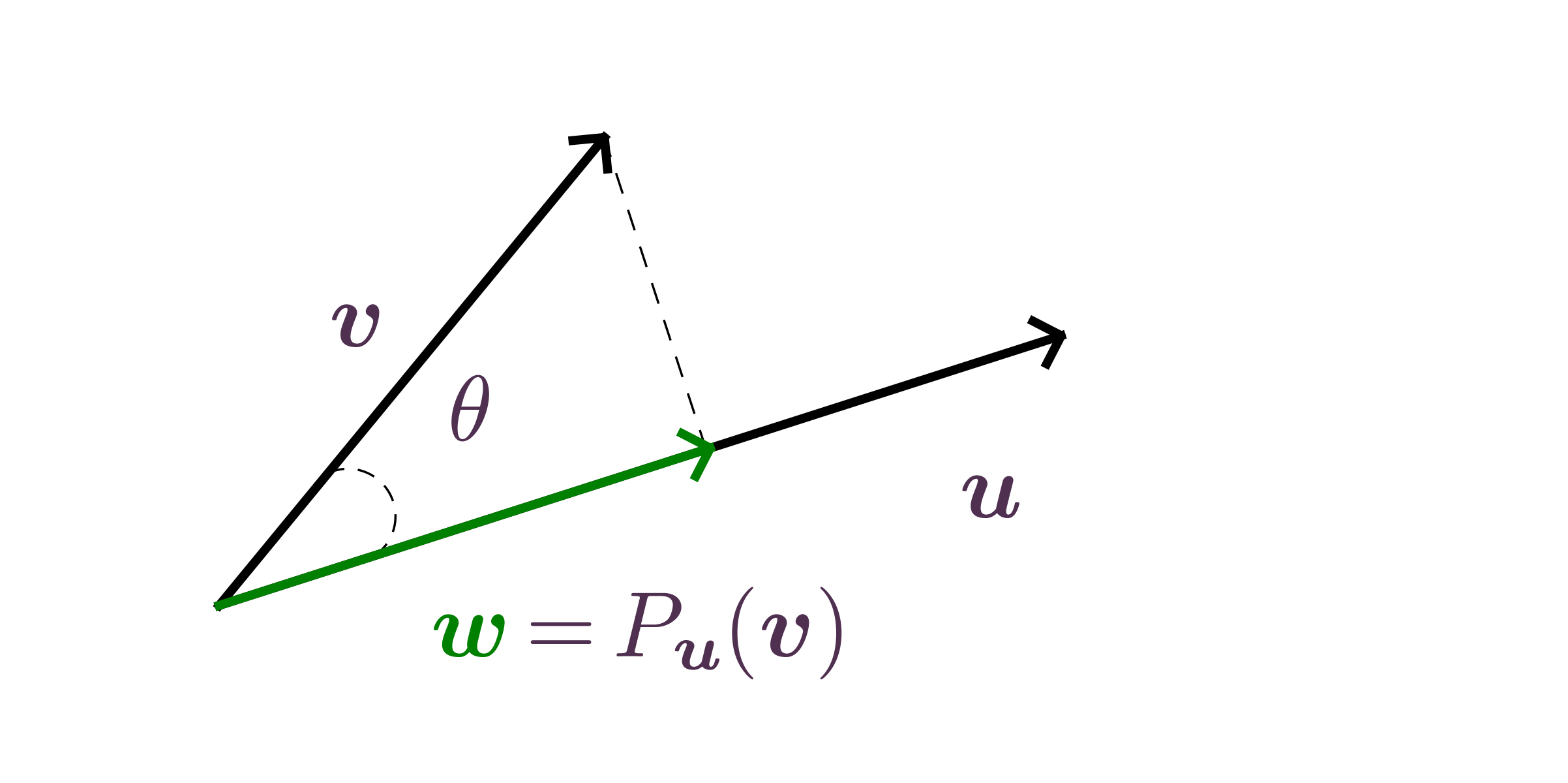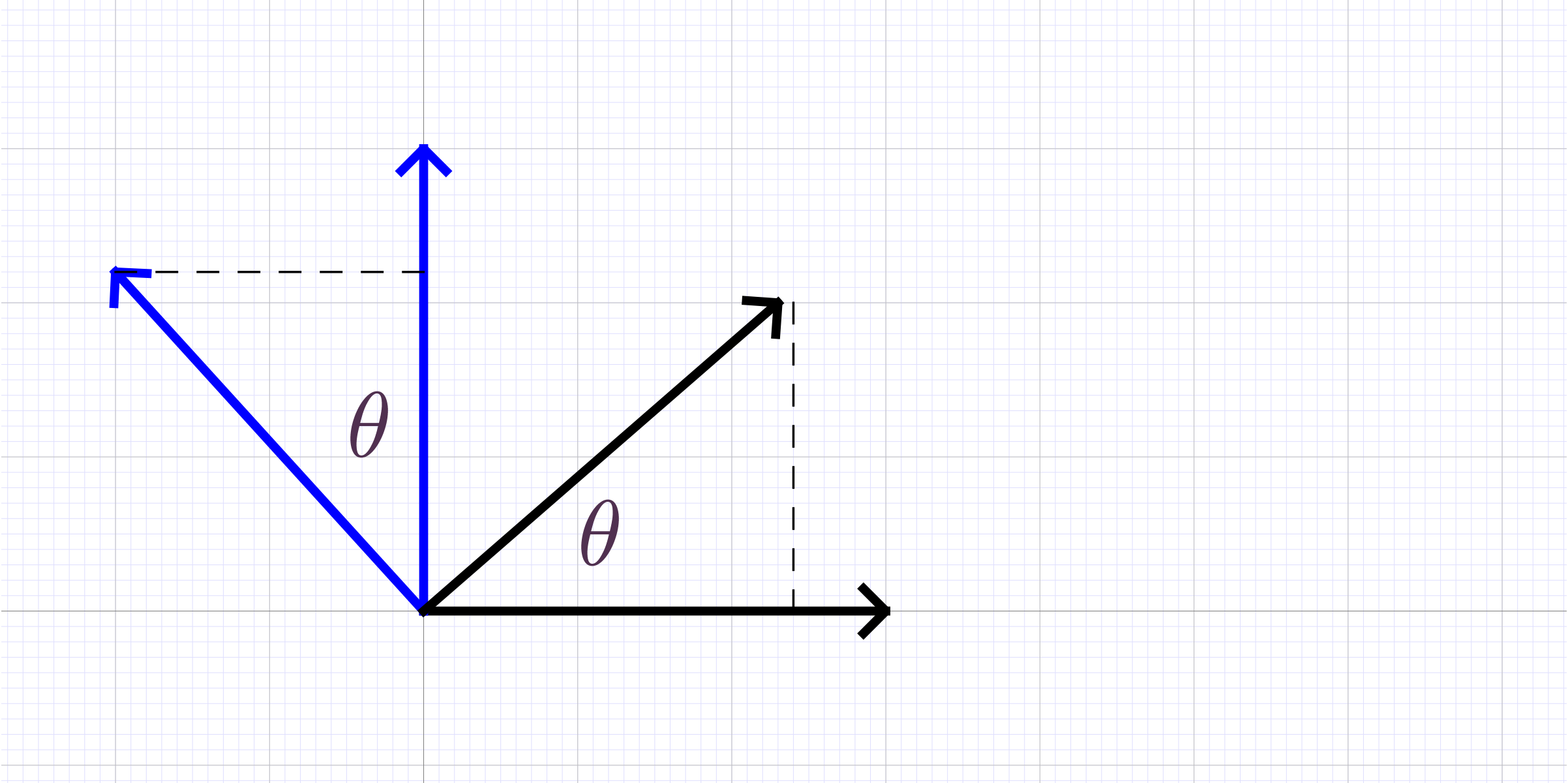Definition. (Relation) . A relation $R$ between two sets $X, Y$ is a subset of the Cartesian product $X \times Y$ , $R \subseteq X \times Y$ .

Definition. (Function) . A function from set $X$ to set $Y$ is a relation $F \subseteq X \times Y$ , that associates to $x \in X$ a single $y \in Y$ .

Common notation $f : X \to Y$ , $f (x) = y$ , $(x, y) \in F \subseteq X \times Y$
Examples: $f : ℝ \to [- 1, 1], f (θ) = \sin θ$ , $g : ℝ \to ℝ_{+}, g (x) = \exp (x) = e^{x}$
Operations defined in $ℝ$ are addition $(+)$ and multiplication $(\cdot)$ . Polynomial functions combine these operations $p_{n} (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{1} x + a_{0}$ .

Definition. (Functional) . A function from vector set $V$ of vector space $𝒱 = (V, S, +, \cdot)$ to scalar set $S$ is a called a functional, $f : V \to S$ .

Definition. (Linear functional) . A mapping that preserves linear combinations $f : V \to S$ , with $f (a 𝒖 + b 𝒗) = a f (𝒖) + b f (𝒗)$ .

Definition. (Mapping) . A function from vector set $U$ of vector space $𝒰 = (U, S, +, \cdot)$ to vector set $V$ of vector space $𝒱 = (V, S, +, \cdot)$ , $𝒇 : U \to V$ .

Definition. (Linear Mapping) . A mapping that preserves linear combinations $𝒇 : U \to V$ , with $𝒇 (a 𝒖 + b 𝒗) = a 𝒇 (𝒖) + b 𝒇 (𝒗)$ .

Linear functionals and mappings are identical to matrices

Linear mappings satisfy $𝒇 (a 𝒖 + b 𝒗) = a 𝒇 (𝒖) + b 𝒇 (𝒗)$
The equation of line is $y = a x + b$ , but $y (x)$ is not a linear mapping if $b \neq 0$
Consider effect of linear mapping upon a vector $𝒙 \in ℝ^{m}$
$𝒇 (𝒙) = 𝒇 (x_{1} 𝒆_{1} + x_{2} 𝒆_{2} + \dots + x_{m} 𝒆_{m}) = x_{1} 𝒇 (𝒆_{1}) + x_{2} 𝒇 (𝒆_{2}) + \dots + x_{m} 𝒇 (𝒆_{m})$
Introduce notation for effect of linear mapping upon column vectors of $𝑰$
$𝒂_{1} = 𝒇 (𝒆_{1}), \dots, 𝒂_{m} = 𝒇 (𝒆_{m})$
Observe that a linear mapping can be expressed as a matrix-vector product
$𝒇 (𝒙) = 𝑨 𝒙$
The mapping $𝒇$ can be identified with the matrix $𝑨$

Measurements: Norm

Definition. The norm of a vector is a function that takes a vector argument, returns a positive real number, $|| || : 𝒱 \to ℝ_{+}$ , and for $𝒖, 𝒗 \in 𝒱$ , $a \in S$ ,satisfies properties:

$|| a 𝒖 || = | a | || 𝒖 ||$

$|| 𝒖 + 𝒗 || ⩽ || 𝒖 || + || 𝒗 ||$

$|| 𝒖 || = 0 \Rightarrow 𝒖 = 𝟎$ .

A norm embodies the concept of measurement of the magnitude of a vector

Different ways of measuring the magnitude of a vector are most appropriate in various applications, resulting in different definitions of a vector norm for $𝒖 \in ℝ^{m}$

1-norm	${\|\| 𝒖 \|\|}_{1} = \sum_{i = 1}^{m} \| u_{i} \|$
2-norm (Euclidean norm)	${\|\| 𝒖 \|\|}_{2} = {(\sum_{i = 1}^{m} u_{i}^{2})}^{1 / 2} = {(𝒖^{T} 𝒖)}^{1 / 2}$
inf-norm	${\|\| 𝒖 \|\|}_{\infty} = {max}_{i \in {1, 2, \dots, m}} \| u_{i} \|$

Different norms are distinguished by subscripts as above. The most commonly used norm is the Euclidean norm that corresponds to the square root of the scalar product, i.e. $|| 𝒖 || = {(𝒖 \cdot 𝒖)}^{1 / 2}$ , in which case the subscript is often suppressed to simplify notation $|| 𝒖 || = {|| 𝒖 ||}_{2}$

Example: Vector norm

∴	u=[1 2 3]; v=[3 0 1]; norm(u)

$3.7416573867739413$

∴	sqrt(dot(u,u))

$3.7416573867739413$

∴	e1=[1 0 0]; e2=[0 1 0]; e3=[0 0 1]; norm(e1)

$1.0$

∴

Measurements: Inner (scalar) product

Scalar products prove to useful in many other contexts than real-valued vectors.

Definition. Consider vectors $𝒖, 𝒗, 𝒘 \in 𝒱$ and scalar $a \in ℝ .$ The function

$⟨, ⟩ : 𝒱 \times 𝒱 \to S$

is a scalar product if:
$⟨ 𝒖, 𝒗 ⟩ = ⟨ 𝒗, 𝒖 ⟩$ (Symmetry)

$⟨ a 𝒖, 𝒗 ⟩ = a ⟨ 𝒖, 𝒗 ⟩, ⟨ 𝒖 + 𝒗, 𝒘 ⟩ = ⟨ 𝒖, 𝒘 ⟩ + ⟨ 𝒗, 𝒘 ⟩$ (Linearity in first argument)

$⟨ 𝒖, 𝒖 ⟩ ⩾ 0, ⟨ 𝒖, 𝒖 ⟩ = 0 \Rightarrow 𝒖 = 𝟎$ (Positive definiteness)
Inner product of $𝒖, 𝒗 \in ℝ^{m}$ , $𝒖 \cdot 𝒗 = u_{1} v_{1} + u_{2} v_{2} + \dots + u_{m} v_{m}$
Preferred expression is through matrix vector multiplication
$𝒖^{T} 𝒗 = [\begin{array}{llll} u_{1} & u_{2} & \dots & u_{m} \end{array}] [\begin{array}{l} v_{1} \\ v_{2} \\ ⋮ \\ v_{m} \end{array}] = 𝒖 \cdot 𝒗 = u_{1} v_{1} + u_{2} v_{2} + \dots + u_{m} v_{m} .$

Example: Inner product of two vectors

∴	u=[1 2 3]; v=[3 0 1]; dot(u,v)

$6$

∴	e1=[1 0 0]; e2=[0 1 0]; e3=[0 0 1]; dot(e1,e2)

$0$

∴	dot(e1,e3)

$0$

∴	dot(e2,e3)

$0$

∴	dot(e1,e1)

$1$

∴

dot(u,e1)

$1$

∴

Measurements: angle between two vectors

Law of cosines
${|| 𝒗 - 𝒘 ||}^{2} = {|| 𝒗 ||}^{2} + {|| 𝒘 ||}^{2} - 2 || 𝒗 || || 𝒘 || \cos (θ)$
Inner product properties
${|| 𝒗 - 𝒘 ||}^{2} = {|| 𝒗 ||}^{2} + {|| 𝒘 ||}^{2} - 2 (𝒗^{T} 𝒘)$
Combine, and define
$\cos (θ) = \frac{𝒗^{T} 𝒘}{|| 𝒗 || || 𝒘 ||}$
In particular if $\cos (θ) = 0 \Rightarrow 𝒗 \cdot 𝒘 = 0$ , $𝒗, 𝒘$ are said to be orthogonal

Example: Angle between two vectors

\cos θ = \frac{𝒖^{T} 𝒗}{|| 𝒖 || || 𝒗 ||}

∴	transpose(e1)*e2/norm(e1)/norm(e2)

$0.0$

∴

acos(0.0)

$1.5707963267948966$

∴	transpose(e1)*e1/norm(e1)/norm(e1)

$1.0$

∴

acos(1)

$0.0$

∴	u=[1; 0]; v=[1; 1]; transpose(u)*v/norm(u)/norm(v)

$0.7071067811865475$

∴	acos(0.7071)/pi*180

$45.00054946652557$

∴

Matrix of a linear transformation

$𝒗 \in ℝ^{n}$ , $𝒗 = 𝑰 𝒗$ , $𝑰 = [\begin{array}{llll} 𝒆_{1} & 𝒆_{2} & \dots & 𝒆_{n} \end{array}]$
$𝒗 = [\begin{array}{llll} 𝒆_{1} & 𝒆_{2} & \dots & 𝒆_{n} \end{array}] [\begin{array}{l} v_{1} \\ v_{2} \\ ⋮ \\ v_{n} \end{array}] = v_{1} 𝒆_{1} + \dots + v_{n} 𝒆_{n} = v_{1} [\begin{array}{l} 1 \\ 0 \\ ⋮ \\ 0 \end{array}] + \dots + v_{n} [\begin{array}{l} 0 \\ ⋮ \\ 0 \\ 1 \end{array}]$
$T : ℝ^{n} \to ℝ^{m}$ a linear mapping (transformation)
$T (𝒗) = T (v_{1} 𝒆_{1} + \dots + v_{n} 𝒆_{n}) = v_{1} T (𝒆_{1}) + \dots + v_{n} T (𝒆_{n})$
Let $𝑨 = [\begin{array}{llll} T (𝒆_{1}) & T (𝒆_{2}) & \dots & T (𝒆_{n}) \end{array}] \in ℝ^{m \times n}$ , $T (𝒗) = 𝑨 𝒗$ . $𝑨$ is the standard matrix of a linear transformation

Stretching transformation

$T$ stretches the $x$ component of $𝒗 \in ℝ^{2}$ by factor $α$ , the $y$ component by $β$
$T (𝒆_{1}) = [\begin{array}{l} α \\ 0 \end{array}], T (𝒆_{2}) = [\begin{array}{l} 0 \\ β \end{array}], 𝑨 = [\begin{array}{ll} T (𝒆_{1}) & T (𝒆_{2}) \end{array}] = [\begin{array}{ll} α & 0 \\ 0 & β \end{array}]$ $T ([\begin{array}{l} 2 \\ 1 \end{array}]) = [\begin{array}{l} 2 α \\ β \end{array}] = [\begin{array}{ll} α & 0 \\ 0 & β \end{array}] [\begin{array}{l} 2 \\ 1 \end{array}]$
In general a diagonal matrix describes stretching with factors $λ_{1}, λ_{2}, \dots, λ_{m} > 0$
$𝑨 = [\begin{array}{llll} λ_{1} & 0 & \dots & 0 \\ 0 & λ_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & λ_{m} \end{array}]$

Projection

Projection of $𝒗 \in ℝ^{m}$ along direction $𝒖 \in ℝ^{m}$ , $|| 𝒖 || = 1$

Figure 1. Projection operation

$𝒘 = (|| 𝒗 || \cos θ) 𝒖 = (|| 𝒗 ||) 𝒖 = (𝒖^{T} 𝒗) 𝒖 = 𝒖 (𝒖^{T} 𝒗) = (𝒖 𝒖^{T}) 𝒗 \Rightarrow$
Projection matrix $𝑷_{𝒖} = 𝒖 𝒖^{T}$

Projection examples

Projection along $𝒆_{1}$ direction in $ℝ^{2}$
$𝑷_{𝒆_{1}} = [\begin{array}{l} 1 \\ 0 \end{array}] [1 \begin{array}{ll} 0 \end{array}] = [\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}], 𝑷_{𝒆_{1}} [\begin{array}{l} x_{1} \\ x_{2} \end{array}] = [\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] = [\begin{array}{l} x_{1} \\ 0 \end{array}] .$
Projection along direction of vector $𝒘 = [\begin{array}{l} 1 \\ 1 \\ 1 \end{array}]$ in $ℝ^{3}$ :
- First obtain a vector of unit norm $𝒖 = 𝒘 / || 𝒘 || = \frac{1}{\sqrt{3}}$ $[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}]$
- Projection matrix
  $𝑷_{𝒖} = 𝒖 𝒖^{T} = \frac{1}{3} [\begin{array}{l} 1 \\ 1 \\ 1 \end{array}] [\begin{array}{lll} 1 & 1 & 1 \end{array}] = \frac{1}{3} [\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}] .$

Reflection

Reflection of $𝒖 \in ℝ^{2}$ across $x_{1}$ axis
$T (𝒆_{1}) = [\begin{array}{l} 1 \\ 0 \end{array}], T (𝒆_{2}) = [\begin{array}{l} 0 \\ - 1 \end{array}], 𝑨 = [\begin{array}{ll} 1 & 0 \\ 0 & - 1 \end{array}], 𝑨 [\begin{array}{l} x_{1} \\ x_{2} \end{array}] = [\begin{array}{l} x_{1} \\ - x_{2} \end{array}] .$

Reflection of $𝒖 \in ℝ^{2}$ across $𝒘 \in ℝ^{2}$ , $|| 𝒘 || = 1$ , $𝒗 = T_{𝒘} (𝒖) = 𝑨 𝒖$ . Two steps:

Project $𝒖$ onto direction of $𝒘$ , $𝒚 = 𝒘 𝒘^{T} 𝒖$ , $𝒚 = 𝒖 + 𝒛$ .
Go from $𝒖$ twice the vector $𝒛$ to obtain the reflection
$𝒗 = 𝑨 𝒖 = 𝒖 + 2 𝒛 = 𝒖 + 2 (𝒚 - 𝒖) = - 𝒖 + 2 𝒘 𝒘^{T} 𝒖 = (2 𝒘 𝒘^{T} - 𝑰) 𝒖$

Figure 2. Reflection matrix diagram $𝑨 = 2 𝒘 𝒘^{T} - 𝑰$ .

Reflection example

Reflect $𝒆_{2}$ across $𝒘 = \frac{1}{\sqrt{2}} [\begin{array}{l} 1 \\ 1 \end{array}] .$
$𝑨 = 2 𝒘 𝒘^{T} - 𝑰 = [\begin{array}{l} 1 \\ 1 \end{array}] [\begin{array}{ll} 1 & 1 \end{array}] - [\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}] = [\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}]$ $𝑨 𝒆_{2} = [\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}] [\begin{array}{l} 0 \\ 1 \end{array}]$

Rotation in

ℝ^{2}

Construct standard rotation matrix by rotating $𝒆_{1}, 𝒆_{2}$

𝑨 = [\begin{array}{ll} T (𝒆_{1}) & T (𝒆_{2}) \end{array}] = [\begin{array}{ll} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array}]

Figure 3. Diagram for construction of rotation matrix

Linear mapping composition, matrix-matrix multiplication

$f : A \to B$ and $g : B \to C$ , a composite function, $h = g \circ f$ , $h : A \to C$ is defined by
$h (x) = g (f (x)) .$
$𝒇 (𝒙) = 𝑨 𝒙, 𝒈 (𝒚) = 𝑩 𝒚, 𝑨 \in ℝ^{m \times n}, 𝑩 \in ℝ^{p \times m}$

$𝒉 (𝒙) = 𝑪 𝒙 = 𝑩 𝑨 𝒙 .$ (1)
Matrix-matrix product is a grouping of matrix-vector products
$𝑪 = [\begin{array}{cccc} 𝒄_{1} & 𝒄_{2} & \dots & 𝒄_{n} \end{array}] = [𝑩 \begin{array}{cccc} 𝒂_{1} & 𝑩 𝒂_{2} & \dots & 𝑩 𝒂_{n} \end{array}] = 𝑩 𝑨$

Transformation composition example: successive rotations in

ℝ^{2}

Consider two transformations $S (𝒖) = 𝑨 𝒖$ , $T (𝒖) = 𝑩 𝒖$ . Composition $S (T (𝒖))$
$R (𝒖) = S (T (𝒖)) = S (𝑩 𝒖) = 𝑨 𝑩 𝒖 = 𝑪 𝒖$
Matrix of transformation composition is product of the individual transformation matrices
Example: Rotation by $φ$ followed by rotation by $θ$ in $ℝ^{2}$
$[\begin{array}{ll} \cos (θ + φ) & - \sin (θ + φ) \\ \sin (θ + φ) & \cos (θ + φ) \end{array}] = [\begin{array}{ll} \cos (θ) & - \sin (θ) \\ \sin (θ) & \cos (θ) \end{array}] [\begin{array}{ll} \cos (φ) & - \sin (φ) \\ \sin (φ) & \cos (φ) \end{array}]$ $\cos (θ + φ) = \cos (θ) \cos (φ) - \sin (θ) \sin (φ)$ $\sin (θ + φ) = \sin (θ) \cos (φ) + \cos (θ) \sin (φ)$

Block matrices

$𝑨 \in ℝ^{4 \times 4}$ is a matrix with 4 rows and 4 columns
$𝑨 = [\begin{array}{llll} 1 & 2 & - 1 & 0 \\ 2 & 1 & 0 & 2 \\ - 1 & 0 & 1 & 2 \\ 0 & 2 & 2 & 1 \end{array}], 𝑫 = [\begin{array}{llll} 1 & - 1 & 1 & 0 \\ - 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & - 1 \\ 0 & 1 & - 1 & 1 \end{array}]$
It is useful to recognize common structures in a matrix
$𝑨 = [\begin{array}{ll} 𝑩 & 𝑪 \\ 𝑪 & 𝑩 \end{array}], 𝑩 = [\begin{array}{ll} 1 & 2 \\ 2 & 1 \end{array}], 𝑪 = [\begin{array}{ll} - 1 & 0 \\ 0 & 2 \end{array}]$ $𝑫 = [\begin{array}{ll} 𝑬 & 𝑭 \\ 𝑭 & 𝑬 \end{array}], 𝑬 = [\begin{array}{ll} 1 & - 1 \\ - 1 & 1 \end{array}], 𝑭 = [\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}]$

Block matrix addition, multiplication, transposition

Matrix block addition
$𝑨 = [\begin{array}{ll} 𝑩 & 𝑪 \\ 𝑪 & 𝑩 \end{array}], 𝑫 = [\begin{array}{ll} 𝑬 & 𝑭 \\ 𝑭 & 𝑬 \end{array}],$ $𝑨 + 𝑫 = [\begin{array}{ll} 𝑩 & 𝑪 \\ 𝑪 & 𝑩 \end{array}] + [\begin{array}{ll} 𝑬 & 𝑭 \\ 𝑭 & 𝑬 \end{array}] = [\begin{array}{ll} 𝑩 + 𝑬 & 𝑪 + 𝑭 \\ 𝑪 + 𝑭 & 𝑩 + 𝑬 \end{array}]$
Matrix block multiplication
$𝑨 𝑫 = [\begin{array}{ll} 𝑩 & 𝑪 \\ 𝑪 & 𝑩 \end{array}] [\begin{array}{ll} 𝑬 & 𝑭 \\ 𝑭 & 𝑬 \end{array}] = [\begin{array}{ll} 𝑩 𝑬 + 𝑪 𝑭 & 𝑩 𝑭 + 𝑪 𝑬 \\ 𝑪 𝑬 + 𝑩 𝑭 & 𝑪 𝑭 + 𝑩 𝑬 \end{array}]$
Matrix block transposition
$𝑴 = [\begin{array}{ll} 𝑼 & 𝑽 \\ 𝑿 & 𝒀 \end{array}], 𝑴^{T} = [\begin{array}{ll} 𝑼^{T} & 𝑿^{T} \\ 𝑽^{T} & 𝒀^{T} \end{array}]$

Transpose of matrix columns

$𝑨 \in ℝ^{m \times n}$ contains $n$ column vectors with $m$ components each
$𝑨 = [\begin{array}{llll} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}]$
The transpose switches rows and columns
$𝑨^{T} = [\begin{array}{l} 𝒂_{1}^{T} \\ 𝒂_{2}^{T} \\ ⋮ \\ 𝒂_{n}^{T} \end{array}] \in ℝ^{n \times m}$
has $n$ rows and $m$ columns

Block operation examples: forming blocks, block assembly

∴	A=[1 2 -1 0; 2 1 0 2; -1 0 1 2; 0 2 2 1]

$[\begin{array}{cccc} 1 & 2 & - 1 & 0 \\ 2 & 1 & 0 & 2 \\ - 1 & 0 & 1 & 2 \\ 0 & 2 & 2 & 1 \end{array}]$ (2)

∴	B=A[1:2,1:2]; C=A[1:2,3:4]; [B C; C B]

$[\begin{array}{cccc} 1 & 2 & - 1 & 0 \\ 2 & 1 & 0 & 2 \\ - 1 & 0 & 1 & 2 \\ 0 & 2 & 2 & 1 \end{array}]$ (3)

∴	D=[1 -1 1 0; -1 1 0 1; 1 0 1 -1; 0 1 -1 1];

∴	E=D[1:2,1:2]; F=D[1:2,3:4]; [D [E F; F E]]

$[\begin{array}{cccccccc} 1 & - 1 & 1 & 0 & 1 & - 1 & 1 & 0 \\ - 1 & 1 & 0 & 1 & - 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & - 1 & 1 & 0 & 1 & - 1 \\ 0 & 1 & - 1 & 1 & 0 & 1 & - 1 & 1 \end{array}]$ (4)

∴

Block operation examples: addition

$𝑨 + 𝑫 = [\begin{array}{ll} 𝑩 & 𝑪 \\ 𝑪 & 𝑩 \end{array}] + [\begin{array}{ll} 𝑬 & 𝑭 \\ 𝑭 & 𝑬 \end{array}] = [\begin{array}{ll} 𝑩 + 𝑬 & 𝑪 + 𝑭 \\ 𝑪 + 𝑭 & 𝑩 + 𝑬 \end{array}]$

∴

A+D

$[\begin{array}{cccc} 2 & 1 & 0 & 0 \\ 1 & 2 & 0 & 3 \\ 0 & 0 & 2 & 1 \\ 0 & 3 & 1 & 2 \end{array}]$ (5)

∴	[B C; C B] + [E F; F E]

$[\begin{array}{cccc} 2 & 1 & 0 & 0 \\ 1 & 2 & 0 & 3 \\ 0 & 0 & 2 & 1 \\ 0 & 3 & 1 & 2 \end{array}]$ (6)

∴

Block operation examples: multiplication

$𝑨 𝑫 = [\begin{array}{ll} 𝑩 & 𝑪 \\ 𝑪 & 𝑩 \end{array}] [\begin{array}{ll} 𝑬 & 𝑭 \\ 𝑭 & 𝑬 \end{array}] = [\begin{array}{ll} 𝑩 𝑬 + 𝑪 𝑭 & 𝑩 𝑭 + 𝑪 𝑬 \\ 𝑪 𝑬 + 𝑩 𝑭 & 𝑪 𝑭 + 𝑩 𝑬 \end{array}]$

∴

A*D

$[\begin{array}{cccc} - 2 & 1 & 0 & 3 \\ 1 & 1 & 0 & 3 \\ 0 & 3 & - 2 & 1 \\ 0 & 3 & 1 & 1 \end{array}]$ (7)

∴	[BE+CF BF+CE; CE+BF CF+BE]

$[\begin{array}{cccc} - 2 & 1 & 0 & 3 \\ 1 & 1 & 0 & 3 \\ 0 & 3 & - 2 & 1 \\ 0 & 3 & 1 & 1 \end{array}]$ (8)

∴

Block operation examples: transposition

$𝑴 = [\begin{array}{ll} 𝑼 & 𝑽 \\ 𝑿 & 𝒀 \end{array}], 𝑴^{T} = [\begin{array}{ll} 𝑼^{T} & 𝑿^{T} \\ 𝑽^{T} & 𝒀^{T} \end{array}]$

∴	M=[1 2 3 4; 5 6 7 8; -1 -2 -3 -4; -5 -6 -7 -8]

$[\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ - 1 & - 2 & - 3 & - 4 \\ - 5 & - 6 & - 7 & - 8 \end{array}]$ (9)

∴	U=M[1:2,1:2]; V=M[1:2,3:4]; X=M[3:4,1:2]; Y=M[3:4,3:4]; M'

$[\begin{array}{cccc} 1 & 5 & - 1 & - 5 \\ 2 & 6 & - 2 & - 6 \\ 3 & 7 & - 3 & - 7 \\ 4 & 8 & - 4 & - 8 \end{array}]$ (10)

∴	[U' X'; V' Y']

$[\begin{array}{cccc} 1 & 5 & - 1 & - 5 \\ 2 & 6 & - 2 & - 6 \\ 3 & 7 & - 3 & - 7 \\ 4 & 8 & - 4 & - 8 \end{array}]$ (11)

∴