MATH347DS L04: Vector space dimension
|
|
Overview
-
Linear dependence and independence
-
Orthogonal, orthonormal vector sets
-
Orthogonal matrices
-
Basis, dimension
-
Realistic application of vector operations framework: ECG
representation and compression
-
Let
be a matrix with
column vectors, each with
components
-
can be
thought of as representing a linear mapping from
to ,
-
Column space, ,
the part of
reachable by linear combination of columns of
-
Left null space, ,
the part of
not reachable by linear combination of columns of
-
Row space, ,
the part of
reachable by linear combination of rows of
-
Null space, ,
the part of
not reachable by linear combination of rows of
Linear dependence and independence: motivating examples
|
|
-
Zero product property of scalar multiplication:
or
-
Matrix-vector counterexamples of zero product property
-
-
-
Matrix-vector example satisfying the zero product property
-
Question: how to distinguish between above examples?
-
Note:
Linear dependence and independence
|
|
Definition.
The vectors are
linearly dependent if there exist scalars, ,
at least one of which is different from zero such that
Note that , with
is a linearly dependent set of vectors since .
The converse of linear dependence is linear independence, a member of
the set cannot be expressed as a non-trivial linear combination of the
other vectors
Definition.
The vectors are
linearly independent if the only
scalars, ,
that satisfy
are ,
,…,.
The choice
that always satisfies (1) is called a trivial
solution. We can restate linear independence as (1)
being satisfied only by the trivial
solution.
Relationship between linear dependence and null space
|
|
Recall:
Definition.
The null space of a
matrix
is the set
|
(2) |
Definition.
The left null space of a
matrix
is the set
|
(3) |
Definition.
The column vectors
of matrix
are orthogonal if
Definition.
The column vectors
of matrix
are orthonormal if
Definition.
The matrix
is orthogonal if
Example. The
reflection matrix across direction ,
in ,is
orthogonal
since .
Suppose in the set spans , .
Adding another vector does not change the span .
Intuitively
contains a redundant vector, it is not a minimal spanning set. Avoid
redundancy by defining minimal spanning sets.
Definition.
A set of vectors
is a basis for vector space if:
-
are linearly independent;
-
.
Adding another vector leads
to a linearly dependent set .
Definition.
The number of vectors
within a basis is the dimension of the vector
space .
Matrix subspace dimensions
|
|
-
the column space of ,
-
the row space of ,
-
the null space of ,
-
the left null space of
, or null
space of ,
.
The dimensions of these subspaces arise so often in applications to
warrant formal definition.
Definition.
The rank of a matrix
is the dimension of its column space.
Definition.
The nullity of a matrix
is the dimension of its null space.
Dimension of column space equals dimension of row space
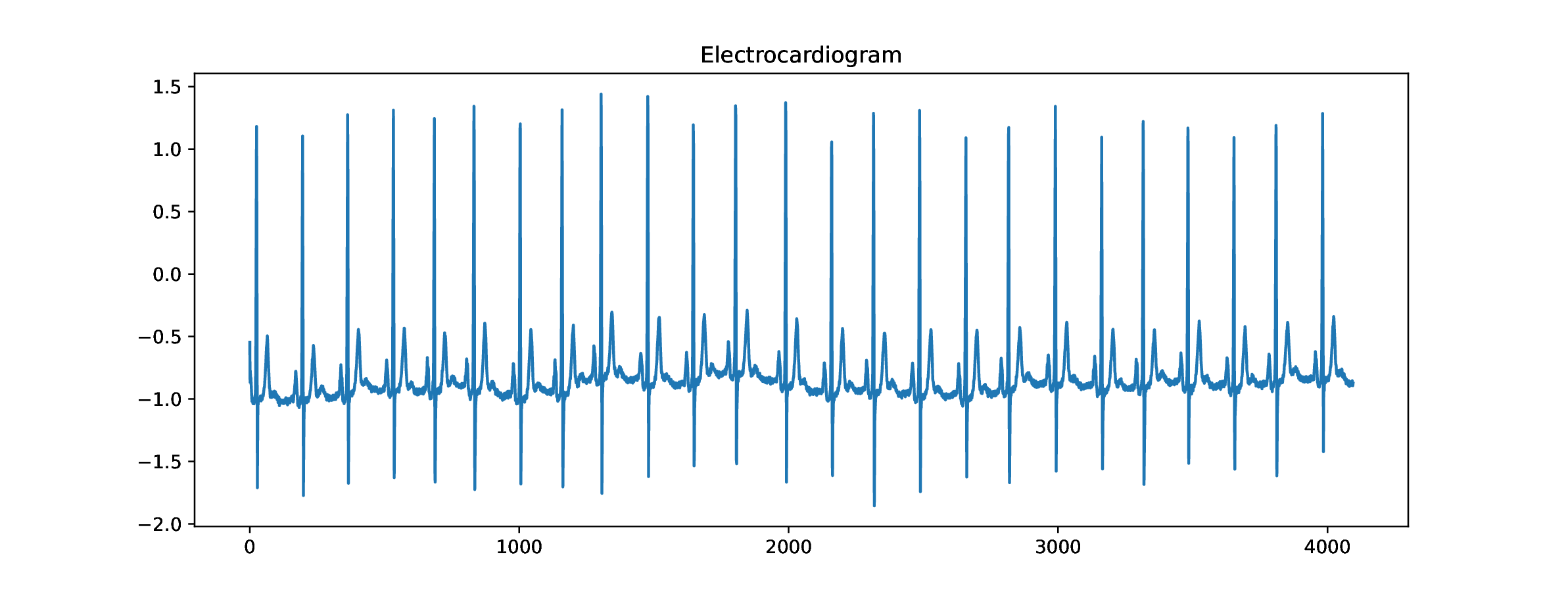
A realistic example: ECG storage and analysis
|
|
∴ |
DataFileName = homedir()*"/courses/MATH347DS/data/ecg/ECGData.mat"; |
∴ |
DataFile = matopen(DataFileName,"r"); |
∴ |
dict = read(DataFile,"ECGData"); |
∴ |
q=12; m=2^q; k=15; b=data[1:m,k]; |
∴ |
figure(1); clf(); plot(b); title("Electrocardiogram"); |
∴ |
cd(homedir()*"/courses/MATH347DS/images"); savefig("S04Fig01.eps"); |
Exterior product construction of
|
|
Definition.
The exterior product of
matrices
and
is the matrix
Matrix structure visualization
|
|
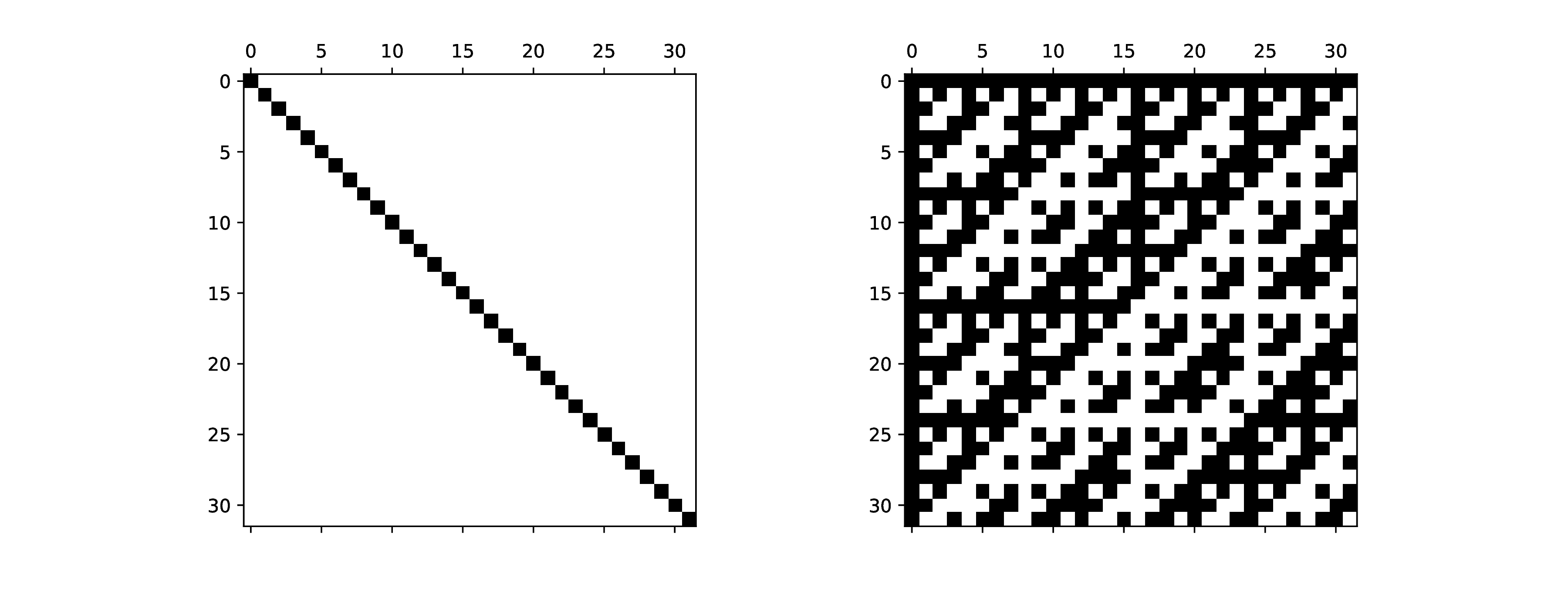 |
|
Figure 1. Structures of ,
|
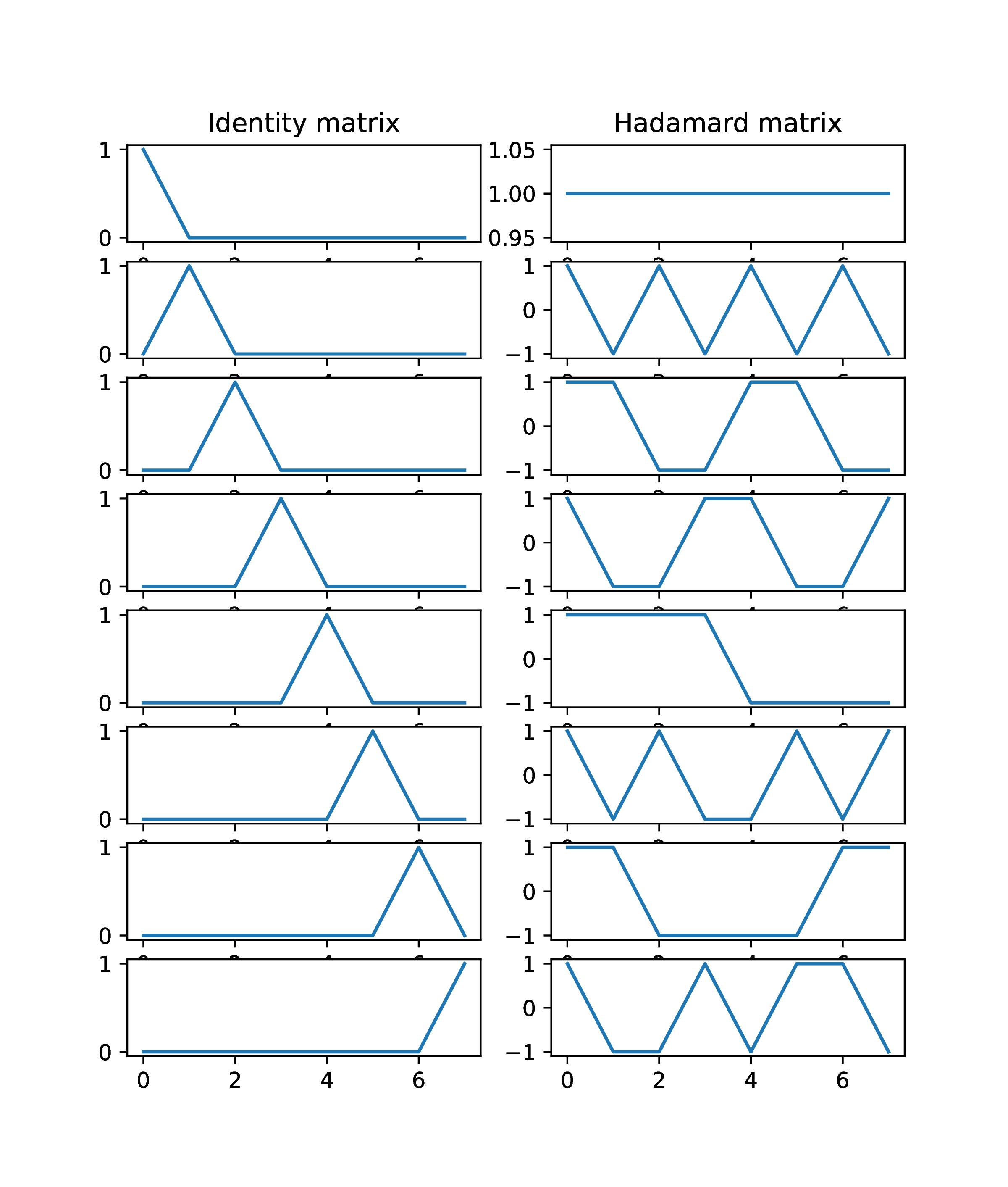 |
|
Figure 2. Comparison of column vectors of
.
|
Vectors of
sample one moment in time, vectors of
sample multiple moments
First attempt at ECG compression
|
|
Results of first attempt at ECG compression
|
|
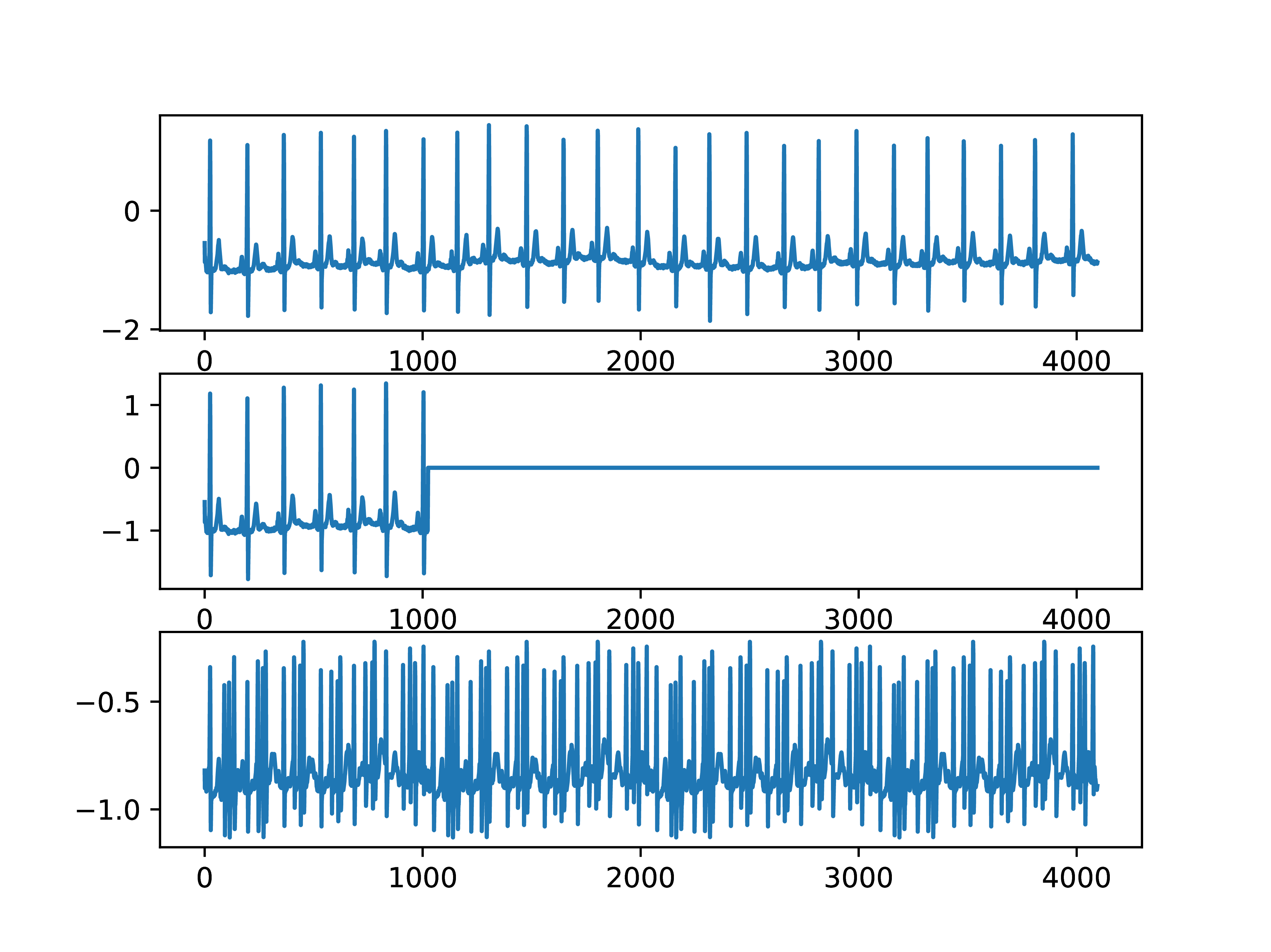 |
|
Figure 3. Top: original ECG, Middle:
Truncation in -basis,
Bottom: Truncation in -basis
|




