MATH347DS L07: Least squares

Overview

• Gram-Schmidt algorithm, $𝑸𝑹$ factorization

• Projection onto subspaces

• Orthogonal projectors

• Best approximation in the 2-norm

• Linear regression

• Polynomial approximation

• Polynomial interpolation

Orthonormal vector sets

Definition. The Dirac delta symbol ${\delta }_{ij}$ is defined as

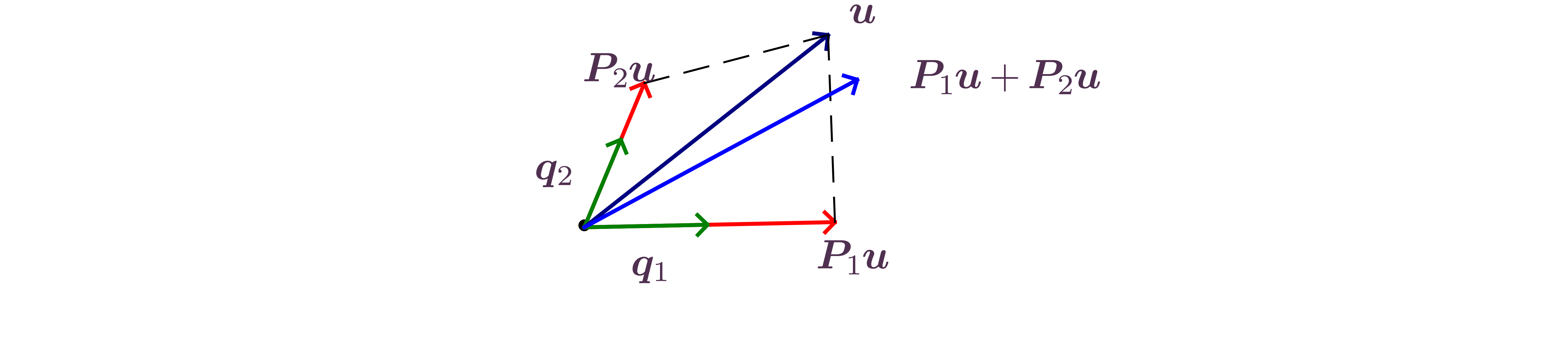
Definition. A set of vectors $\{{𝒖}_1,\dots ,{𝒖}_n\}$ is said to be orthonormal if

• The column vectors of the identity matrix are orthonormal

Gram-Schmidt algorithm

• An arbitrary vector set can be transformed into an orthonormal set by the Gram-Schmidt algorithm

• Idea:

  • Start with an arbitrary direction ${𝒂}_1$

  • Divide by its norm to obtain a unit-norm vector ${𝒒}_1={𝒂}_1/||{𝒂}_1||$

  • Choose another direction ${𝒂}_2$

  • Subtract off its component along previous direction(s) ${𝒂}_2-\left({𝒒}_1^T{𝒂}_2\right){𝒒}_1$

  • Divide by norm ${𝒒}_2=({𝒂}_2-\left({𝒒}_1^T{𝒂}_2\right){𝒒}_1)/||{𝒂}_2-\left({𝒒}_1^T{𝒂}_2\right){𝒒}_1||$

  • Repeat the above

Matrix formulation of Gram-Schmidt ($𝑸𝑹$ factorization)

• Consider $𝑨\in {ℝ}^{m\times n}$ with linearly independent columns. By linear combinations of the columns of $𝑨$ a set of orthonormal vectors ${𝒒}_1,\dots ,{𝒒}_n$ will be obtained. This can be expressed as a matrix product

  ${\displaystyle 𝑨=\left(\begin{array}{cccc}{𝒂}_1& {𝒂}_2& \dots & {𝒂}_n\end{array}\right)=\left(\begin{array}{cccc}{𝒒}_1& {𝒒}_2& \dots & {𝒒}_n\end{array}\right)\left(\begin{array}{ccccc}{r}_{11}& r_{12}& r_{13}& \dots & r_{1n}\\ 0& r_{22}& r_{23}& \dots & r_{2n}\\ 0& 0& r_{33}& \dots & r_{3n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & \dots & r_{mn}\end{array}\right)=𝑸𝑹}$

  with $𝑸\in {ℝ}^{m\times n}$, $𝑹\in {ℝ}^{n\times n}$. The matrix $𝑹$ is upper-triangular (also referred to as right-triangular) since to find vector ${𝒒}_1$ only vector ${𝒂}_1$ is used, to find vector ${𝒒}_2$ only vectors ${𝒂}_1,{𝒂}_2$ are used

• The above is equivalent to the system

  ${\displaystyle \{\begin{array}{l}{𝒂}_1=r_{11}{𝒒}_1\\ {𝒂}_2=r_{12}{𝒒}_1+r_{22}{𝒒}_2\\ ⋮\\ {𝒂}_n=r_{1n}{𝒒}_1+r_{2n}{𝒒}_2+\dots +r_{nn}{𝒒}_n\end{array}}$

Matrix formulation of Gram-Schmidt ($𝑸𝑹$ factorization)

• The system can be solved to find $𝑹,𝑸$ by:

  1. Imposing $||{𝒒}_1||=1\Rightarrow r_{11}=||{𝒂}_1||$, ${𝒒}_1=a_1/r_{11}$

  2. Computing projections of ${𝒂}_2,\dots ,{𝒂}_n$ along ${𝒒}_1$

     ${\displaystyle r_{12}={𝒒}_1^T{𝒂}_2,\dots ,r_{1n}={𝒒}_1^T{𝒂}_n}$

  3. Subtracting components along ${𝒒}_1$ from ${𝒂}_2,\dots ,{𝒂}_n$

     ${\displaystyle \{\begin{array}{l}{𝒂}_2-r_{12}{𝒒}_1=r_{22}{𝒒}_2\\ ⋮\\ {𝒂}_n-r_{1n}{𝒒}_1=r_{2n}{𝒒}_2+\dots +r_{nn}{𝒒}_n\end{array}}$

  4. The above steps reduced the size of the system by 1. Repeating the steps completes the solution. The overall process is known as the Gram-Schmidt algorithm

$𝑸𝑹$ factorization

• For $𝑨\in {ℝ}^{m\times n}$ with linearly independent columns, the Gram-Schmidt algorithm furnishes a factorization

  ${\displaystyle 𝑸𝑹=𝑨}$

  with $𝑸\in {ℝ}^{m\times n}$ with orthonormal columns and $𝑹\in {ℝ}^{n\times n}$ an upper triangular matrix.

• Since the column vectors within $𝑸$ were obtained through linear combinations of the column vectors of $𝑨$ we have

  ${\displaystyle C\left(𝑨\right)=C\left(𝑸\right)}$

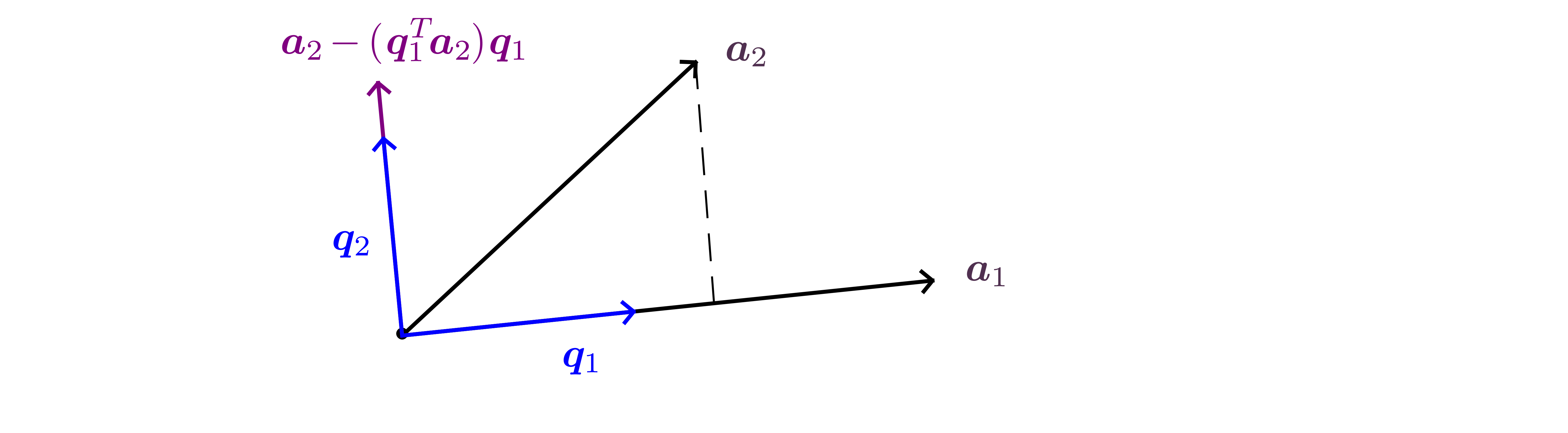
Orthogonal projection of a vector along another vector

• Consider a vector $𝒖\in {ℝ}^m$, and a unit-norm vector ${𝒒}_1\in {ℝ}^m$

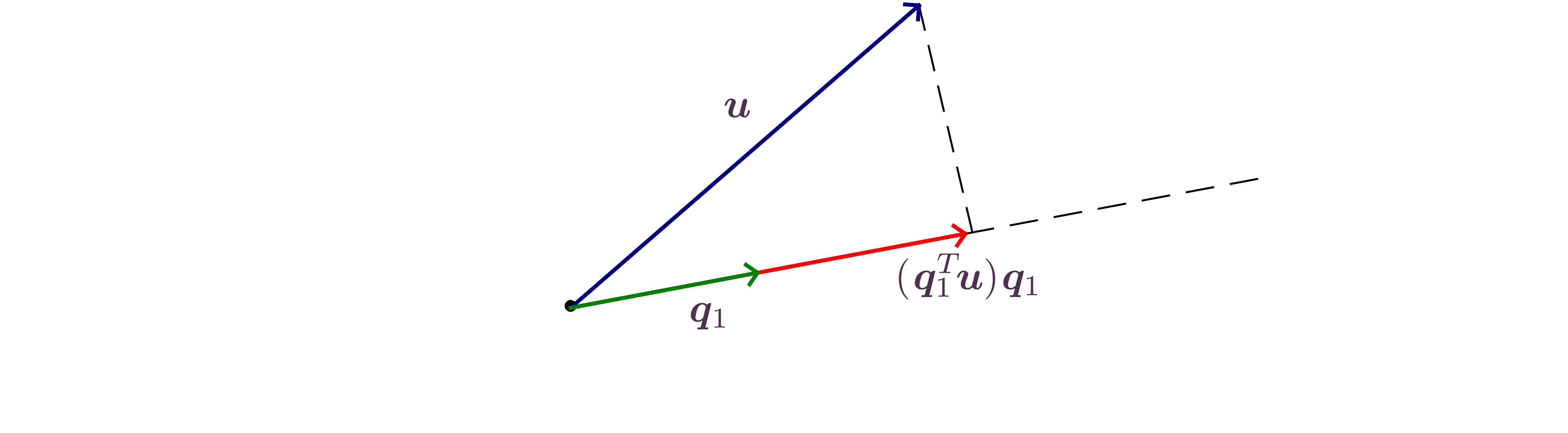
Definition. The orthogonal projection of $𝒖\in {ℝ}^m$ along direction ${𝒒}_1\in {ℝ}^m$, $||{𝒒}_1||=1$ is the vector $\left({𝒒}_1^T𝒖\right){𝒒}_1$.

• Scalar-vector multiplication commutativity: $\left({𝒒}_1^T𝒖\right){𝒒}_1={𝒒}_1\left({𝒒}_1^T𝒖\right)$

• Matrix multiplication associativity: ${𝒒}_1\left({𝒒}_1^T𝒖\right)=\left({𝒒}_1{𝒒}_1^T\right)𝒖={𝑷}_1𝒖$, with ${𝑷}_1\in {ℝ}^{m\times m}$

Definition. The matrix ${𝑷}_1={𝒒}_1{𝒒}_1^T\in {ℝ}^{m\times m}$ is the orthogonal projector along direction ${𝒒}_1\in {ℝ}^m$, $||{𝒒}_1||=1$.

Orthogonal projection onto a subspace

• Consider $n$ orthonormal vectors grouped into a matrix $𝑸=\left(\begin{array}{lll}{𝒒}_1& \dots & {𝒒}_n\end{array}\right)\in {ℝ}^{m\times n}$

• The orthogonal projection of $𝒖$ onto the subspace spanned by ${𝒒}_1,\dots ,{𝒒}_n$ is

  ${\displaystyle 𝑷𝒖={𝑷}_1𝒖+\dots +{𝑷}_n𝒖=\left({𝒒}_1{𝒒}_1^T\right)𝒖+\dots {+}_{}\left({𝒒}_n{𝒒}_n^T\right)𝒖\Rightarrow }$ ${\displaystyle 𝑷={𝒒}_1{𝒒}_1^T+\dots +{𝒒}_n{𝒒}_n^T=\left(\begin{array}{ccc}{𝒒}_1& \dots & {𝒒}_n\end{array}\right)\left(\begin{array}{c}{𝒒}_1^T\\ ⋮\\ {𝒒}_n^T\end{array}\right)=𝑸{𝑸}^T}$

  Definition. The orthogonal projector onto $C\left(𝑸\right)$, $𝑸\in {ℝ}^{m\times n}$ with orthonormal column vectors is $𝑷=𝑸{𝑸}^T$

Complementary orthogonal projector

• Given $𝒖\in {ℝ}^m$ and $𝑸=\left(\begin{array}{lll}{𝒒}_1& \dots & {𝒒}_n\end{array}\right)\in {ℝ}^{m\times n}$ with orthonormal columns

Definition. The complementary orthogonal projector to $𝑷=𝑸{𝑸}^T$ is $𝑰-𝑷$, where $𝑸\in {ℝ}^{m\times n}$ is a matrix with orthonormal columns.

• The complementary orthogonal projector projects a vector onto the left null space, $N\left({𝑸}^T\right)$

Orthogonal projectors and linear systems

• Consider the linear system $𝑨𝒙=𝒃$ with $𝑨\in {ℝ}^{m\times n}$, $𝒙\in {ℝ}^n$, $𝒃\in {ℝ}^m$. Orthogonal projectors and knowledge of the four fundamental matrix subspaces allows us to succintly express whether there exist no solutions, a single solution of an infinite number of solutions:

  • Consider the factorization $𝑸𝑹=𝑨$, the orthogonal projector $𝑷=𝑸{𝑸}^T$, and the complementary orthogonal projector $𝑰-𝑷$

  • If $||(𝑰-𝑷)𝒃||\ne 0$, then $𝒃$ has a component outside the column space of $𝑨$, and $𝑨𝒙=𝒃$ has no solution

  • If $||(𝑰-𝑷)𝒃||=0$, then $𝒃\in C\left(𝑸\right)=C\left(𝑨\right)$ and the system has at least one solution

  • If $N\left(𝑨\right)=\left\{𝟎\right\}$ (null space only contains the zero vector, i.e., null space of dimension 0) the system has a unique solution

  • If $\dim N\left(𝑨\right)=n-r>0$, then a vector $𝒚\in N\left(𝑨\right)$ in the null space is written as

    ${\displaystyle 𝒚=c_1{𝒛}_1+\dots +c_{n-r}{𝒛}_{n-r}}$

    and if $𝒙$ is a solution of $𝑨𝒙=𝒃$, so is $𝒙+𝒚$, since

    ${\displaystyle 𝑨(𝒙+𝒚)=𝑨𝒙+c_1𝑨{𝒛}_1+\dots +c_{n-r}𝑨{𝒛}_{n-r}=𝒃+𝟎+\dots +𝟎=𝒃}$

    The linear system has an $(n-r)$-parameter family of solutions

Best approximation in the 2-norm (least squares)

Figure 1. Least squares problem: find $𝒗\in C\left(𝑨\right)$, $𝑨\in {ℝ}^{m\times n}$ closest to some given $𝒚$ in the 2-norm

• Mathematical statement: solve the minimization problem ${min}_{𝒄\in {ℝ}^n}||𝒚-𝑨𝒄||$

• Approach: project $𝒚$ onto the column space of $𝑨$:

  1. Find an orthonormal basis for column space of $𝑨$ by $𝑸𝑹$ factorization, $𝑸𝑹=𝑨$

  2. State that $𝒗$ is the projection of $𝒚$, $𝒗={𝑷}_{C\left(𝑨\right)}𝒚={𝑷}_{𝑸}𝒚=𝑸{𝑸}^T𝒚$

  3. State that $𝒗$ is within the column space of $𝑨$, $𝒗=𝑨𝒄=𝑸𝑹𝒄$

  4. Set equal the two expressions of $𝒗$, $$$𝑸{𝑸}^T𝒚=𝑸𝑹𝒄\Rightarrow 𝑹𝒄={𝑸}^T𝒚$

  5. Solve the triangular system to find $𝒄$ (in Julia, Matlab, Octave: c=R\(Q'y))

Least squares: linear regression calculus approach

• In many scientific fields the problem of determining the straight line $y\left(x\right)=c_0+c_{1}x$, that best approximate data $𝒟=\{(x_i,y_i),i=1,\dots ,m\}$ arises. The problem is to find the coefficients $c_0,c_1$, and this is referred to as the linear regression problem.

• The calculus approach: Form sum of squared differences between $y\left(x_i\right)$ and $y_i$

  ${\displaystyle S(c_0,c_1)=\sum _{i=1}^m{(y\left(x_i\right)-y_i)}^2=\sum _{i=1}^m{(c_0+c_1{x}_i-y_i)}^2}$

  and seek $(c_0,c_1)$ that minimize $S(c_0,c_1)$ by solving the equations

  ${\displaystyle \frac{\partial S}{\partial c_0}=0\Rightarrow 2\sum _{i=1}^m(c_0+c_1{x}_i-y_i)=0\iff m{c}_0+\left(\sum _{i=1}^m{x}_i\right)c_1=\sum _{i=1}^m{y}_i}$ ${\displaystyle \frac{\partial S}{\partial c_1}=0\Rightarrow 2\sum _{i=1}^m(c_0+c_1{x}_i-y_i)x_i=0\iff \left(\sum _{i=1}^m{x}_i\right)c_0+\left(\sum _{i=1}^m{x}_i^2\right)c_1=\sum _{i=1}^m{x}_i{y}_i}$

Geometry of linear regression: normal equations

• If $𝑸𝑹=𝑨$ is known, preferable to solve $𝑸{𝑸}^T𝒚=𝑸𝑹𝒄\Rightarrow 𝑹𝒄={𝑸}^T𝒚$.

Linear regression example

1. Generate some data on a line and perturb it by some random quantities

   ∴	m=100; x=(0:m-1)./m; c0=2; c1=3; yex=c0.+c1*x; y=(yex.+rand(m,1).-0.5);

   ∴

2. Form the $𝑸,𝑹$ matrices, $𝑸𝑹=𝑨$, (qr(A,0))

   ∴	A=ones(m,2); A[:,2]=x[:]; QR=qr(A); Q=QR.Q[:,1:2]; R=QR.R[1:2,1:2];

   ∴

3. Solve the system $𝑹𝒙={𝑸}^T𝒚$

   ∴	c = R\(transpose(Q)*y)

   ${\displaystyle \left[\begin{array}{c}1.9812089298039193\\ 2.9758677046339135\end{array}\right]}$

   (1)

   ∴

4. Form the linear combination $𝒗=𝑨𝒙$ closest to $𝒃$

   ∴

   v=A*c;

   ∴

Linear regression result

• Plot the perturbed data (black dots), the result of the linear regression (green circles), as well as the line used to generate yex (red line)

  ∴	plot(x,y,".k",x,v,"og",x,yex,"r"); title("Linear regression"); xlabel("x"); ylabel("y,v,yex");

  ∴	cd(homedir()*"/Desktop/courses/MATH347DS/images"); savefig("L07Fig02.eps");

  ∴

Figure 2. Linear reqression through least squares result

Quadratic regression

• The calculus approach becomes complex for higher-degree approximation

  ${\displaystyle y\left(x\right)=c_0+c_{1}x+c_2{x}^2=\left[\begin{array}{lll}1& x& x^2\end{array}\right]\left[\begin{array}{l}{c}_0\\ c_1\\ c_2\end{array}\right]=A\left(x\right)𝒄.}$

  Note that $y\left(x\right)$ is nonlinear.

• The least squares approach retains its simplicity since but $y(c_0,c_1,c_2)$ is linear.

  ∴	m=100; x=(0:m-1)./m; c0=2; c1=3; c2=-5; yex=c0.+c1*x.+c2*x.^2;

  ∴	y=(yex.+rand(m,1).-0.5);

  ∴	A=ones(m,3); A[:,2]=x[:]; A[:,3]=x[:].^2; QR=qr(A); Q=QR.Q[:,1:3]; R=QR.R[1:3,1:3];

  ∴	c = R\(transpose(Q)*y)

  ${\displaystyle \left[\begin{array}{c}2.019352129655483\\ 2.8933875491171213\\ -4.773241628594068\end{array}\right]}$

  (2)

  ∴

  v=A*c;

  ∴

Quadratic regression result

• Plot the perturbed data (black dots), the result of the linear regression (green circles), as well as the line used to generate yex (red line)

  ∴	plot(x,y,".k",x,v,"og",x,yex,"r"); title("Quadratic regression"); xlabel("x"); ylabel("y,v,yex");

  ∴	cd(homedir()*"/Desktop/courses/MATH347DS/images"); savefig("L07Fig03.eps");

  ∴

Figure 3. Linear reqression through least squares result

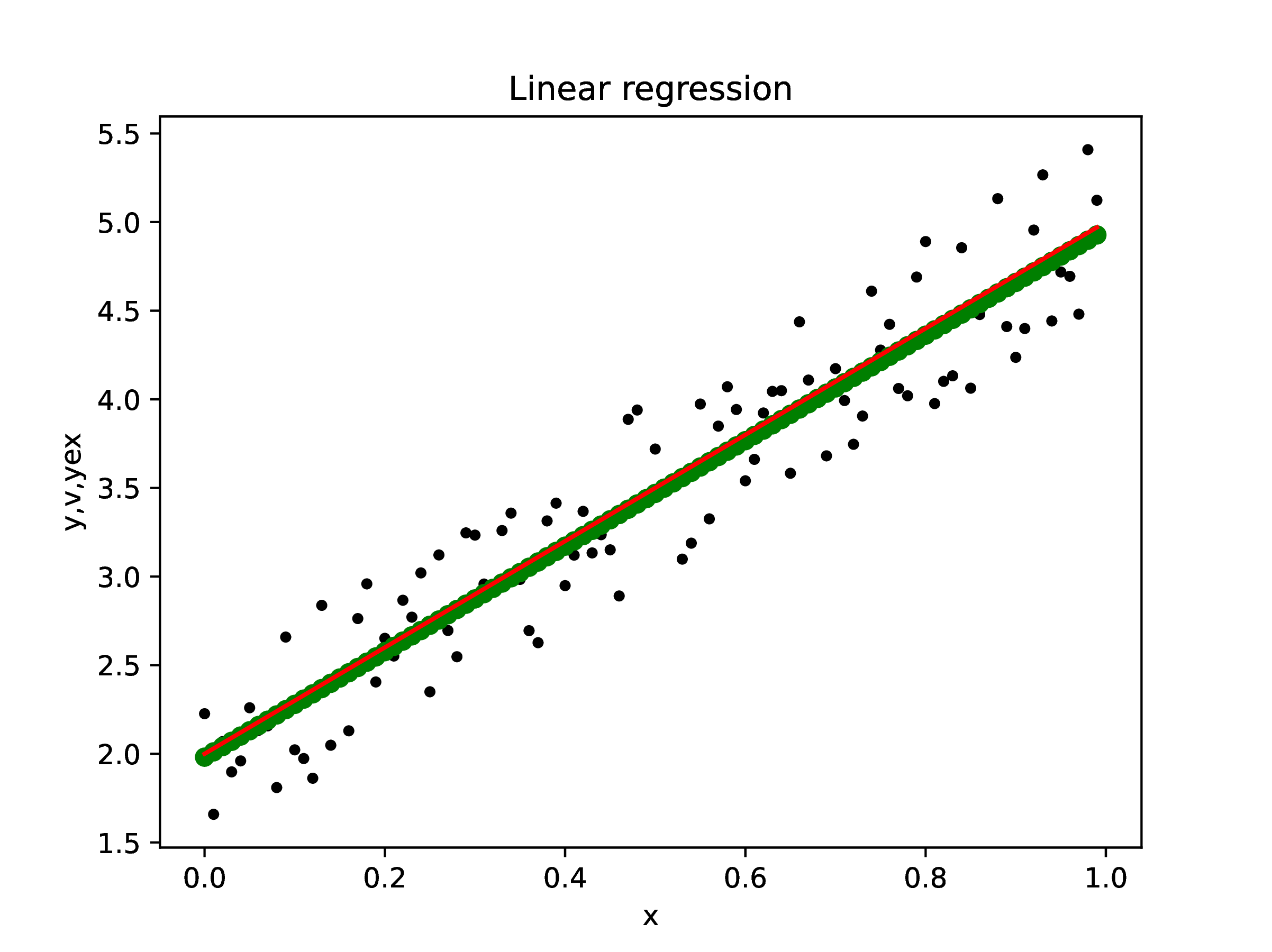
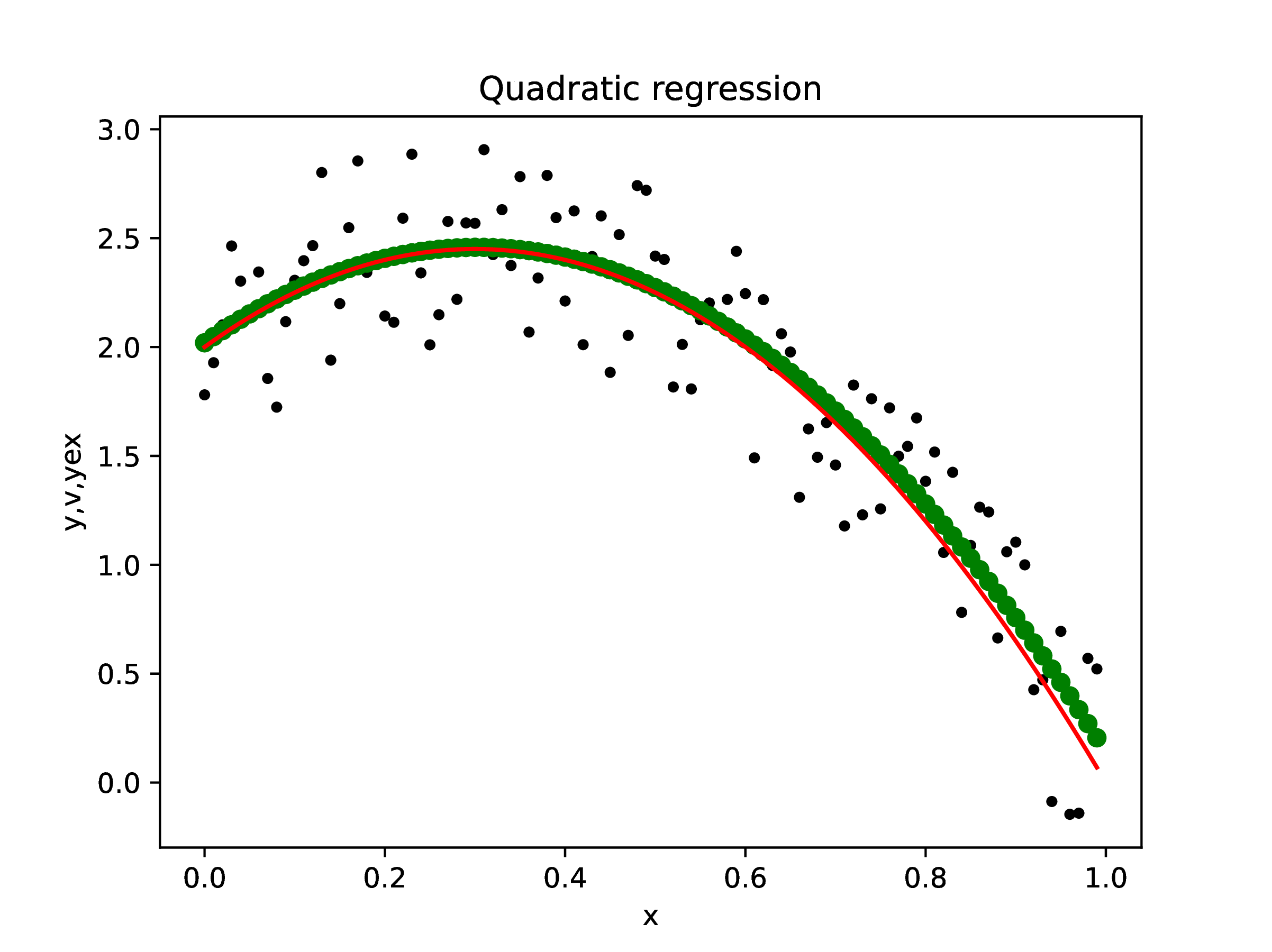
The $m=n$ case: polynomial interpolation

Definition. The polynomial interpolant of data $𝒟=\{(x_i,y_i),i=1,\dots ,m\}$ with $x_i\ne x_j$ if $i\ne j$ is a polynomial of degree $m-1$

that satisfies the conditions $p_{m-1}\left(x_i\right)=y_i$, $i=1,\dots ,m$.

• We can apply the same approach. In this particular case, the error $𝒆$ can be made zero.

∴ 

m=3; x=(0:m-1)./m; c0=2; c1=3; c2=-5; yex=c0.+c1*x.+c2*x.^2;

∴ 

A=ones(m,3); A[:,2]=x[:]; A[:,3]=x[:].^2; QR=qr(A); Q=QR.Q[:,1:3]; R=QR.R[1:3,1:3];

∴ 

c = R\(transpose(Q)*yex)

Note that the coefficients used to generate the data are recovered exactly.