MATH347DS L09: Eigenproblems

Overview

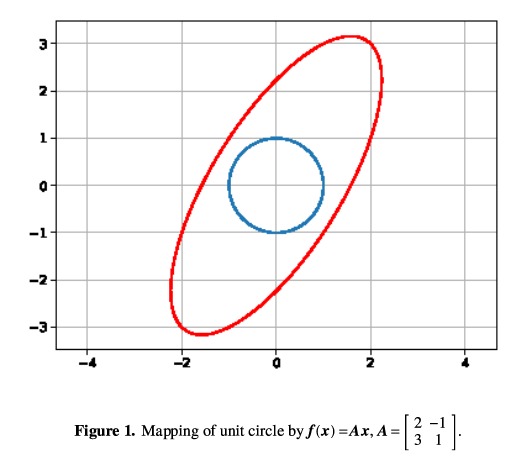
• Determinants

  • geometric interpretation

  • computation rules

• Characteristic polynomial

  • repeated roots, algebraic multiplicity

• Eigenspaces

  • null space dimension, geometric multiplicity

• Eigendecomposition

  • possible if algebraic multiplicity equals geometric multiplicity for each eigenvalues

  • simple, meaning, an orthogonal or unitary decomposition for normal matrices

• Computing the SVD reduces to computing two eigenproblems

Geometric definition

Definition. The determinant of a square matrix $𝑨=\left[\begin{array}{lll}{𝒂}_1& \dots & {𝒂}_m\end{array}\right]\in {ℝ}^{m\times m}$

is a real number giving the (oriented) volume of the parallelepiped spanned by matrix column vectors.

• $m=2$

  ${\displaystyle 𝑨=\left[\begin{array}{ll}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right],\det \left(𝑨\right)=\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|.}$

• $m=3$

  ${\displaystyle 𝑨=\left[\begin{array}{lll}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right],\det \left(𝑨\right)=\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|.}$

Determinants of $m=2$, $m=3$ size matrices

• Computation of a determinant with $m=2$

  ${\displaystyle \left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|=a_{11}{a}_{22}-a_{12}{a}_{21}}$

• Computation of a determinant with $m=3$

  ${\displaystyle \begin{array}{rcl}\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|& =& a_{11}{a}_{22}{a}_{33}+a_{21}{a}_{32}{a}_{13}+a_{31}{a}_{12}{a}_{23}\\ & & -a_{13}{a}_{22}{a}_{31}-a_{23}{a}_{32}{a}_{11}-a_{33}{a}_{12}{a}_{21}\end{array}}$

• Where do these determinant computation rules come from? Two viewpoints

  • Geometric viewpoint: determinants express parallelepiped volumes

  • Algebraic viewpoint: determinants are computed from all possible products that can be formed from choosing a factor from each row and each column

Determinant in 2D gives area of parallelogram

• $m=2$

  

• In two dimensions a “parallelepiped” becomes a parallelogram with area given as

  ${\displaystyle \left(\mathrm{Area}\right)=(\mathrm{Length}\mathrm{of}\mathrm{Base})\times (\mathrm{Length}\mathrm{of}\mathrm{Height})}$

• Take ${𝒂}_1$ as the base, with length $b=||{𝒂}_1||$. Vector ${𝒂}_1$ is at angle ${\phi }_1$ to $x_1$-axis, ${𝒂}_2$ is at angle ${\phi }_2$ to $x_2$-axis, and the angle between ${𝒂}_1$, ${𝒂}_2$ is $\theta ={\phi }_2-{\phi }_1$. The height has length

  ${\displaystyle h=||{𝒂}_2||\sin \theta =||{𝒂}_2||\sin .(.{\phi }_2-{\phi }_1)=||{𝒂}_2||(\sin {\phi }_2\cos {\phi }_1-\sin {\phi }_1\cos {\phi }_2)}$

• Use $\cos {\phi }_1=a_{11}/||{𝒂}_1||$, $\sin {\phi }_1=a_{12}/||{𝒂}_1||$, $\cos {\phi }_2=a_{21}/||{𝒂}_2||$, $\sin {\phi }_2=a_{22}/||{𝒂}_2||$

  ${\displaystyle \left(\mathrm{Area}\right)=||{𝒂}_1||||{𝒂}_2||(\sin {\phi }_2\cos {\phi }_1-\sin {\phi }_1\cos {\phi }_2)=a_{11}{a}_{22}-a_{12}{a}_{21}}$

Determinant calculations

• The geometric interpretation of a determinant as an oriented volume is useful in establishing rules for calculation with determinants:

  • Determinant of matrix with repeated columns is zero (since two edges of the parallelepiped are identical). Example for $m=3$

    ${\displaystyle \Delta =\left|\begin{array}{ccc}a& a& u\\ b& b& v\\ c& c& w\end{array}\right|=abw+bcu+cav-ubc-vca-wab=0}$

    This is more easily seen using the column notation

    ${\displaystyle \Delta =\det \left(\begin{array}{cccc}{𝒂}_1& {𝒂}_1& {𝒂}_3& \dots \end{array}\right)=0}$

  • Determinant of matrix with linearly dependent columns is zero (since one edge lies in the 'hyperplane' formed by all the others)

Determinant calculation rules

• Separating sums in a column (similar for rows)

  ${\displaystyle \det \left(\begin{array}{cccc}{𝒂}_1+{𝒃}_1& {𝒂}_2& \dots & {𝒂}_m\end{array}\right)=\det \left(\begin{array}{cccc}{𝒂}_1& {𝒂}_2& \dots & {𝒂}_m\end{array}\right)+\det \left(\begin{array}{cccc}{𝒃}_1& {𝒂}_2& \dots & {𝒂}_m\end{array}\right)}$

  with ${𝒂}_i,{𝒃}_1\in {ℝ}^m$

• Scalar product in a column (similar for rows)

  ${\displaystyle \det \left(\begin{array}{cccc}\alpha {𝒂}_1& {𝒂}_2& \dots & {𝒂}_m\end{array}\right)=\alpha \det \left(\begin{array}{cccc}{𝒂}_1& {𝒂}_2& \dots & {𝒂}_m\end{array}\right)}$

  with $\alpha \in ℝ$

• Linear combinations of columns (similar for rows)

  ${\displaystyle \det \left(\begin{array}{cccc}{𝒂}_1& {𝒂}_2& \dots & {𝒂}_m\end{array}\right)=\det \left(\begin{array}{cccc}{𝒂}_1& \alpha {𝒂}_1+{𝒂}_2& \dots & {𝒂}_m\end{array}\right)}$

  with $\alpha \in ℝ$.

Determinant of transpose, matrix product, non-full rank matrices

• $\det \left(𝑨\right)=\det \left({𝑨}^T\right)$

• $\det (𝑨𝑩)=\det \left(𝑨\right)\det \left(𝑩\right)$

• $𝑨\in {ℝ}^{m\times m}$, if $\mathrm{rank}\left(𝑨\right)<m$ then $\det \left(𝑨\right)=0$

The eigenvalue problem

• For square matrix $𝑨\in {ℝ}^{m\times m}$ find non-zero vectors whose directions are not changed by multiplication by $𝑨$, $𝑨𝒙=\lambda 𝒙$, $\lambda$ is scalar, the eigenvalue problem.

• Consider the eigenproblem $𝑨𝒙=\lambda 𝒙$ for $𝑨\in {ℝ}^{m\times m}$. Rewrite as

  ${\displaystyle 𝑨𝒙=\lambda 𝒙\Rightarrow (𝑨-\lambda 𝑰)𝒙=𝟎.}$

  Since $𝒙\ne 𝟎$, a solution to eigenproblem exists only if $𝑨-\lambda 𝑰$ is singular.

• $𝑨-\lambda 𝑰$ singular implies $\det (𝑨-\lambda 𝑰)=0$.

• Investigate form of $\det (𝑨-\lambda 𝑰)=0$

  ${\displaystyle \det (𝑨-\lambda 𝑰)=\left|\begin{array}{ccccc}{a}_{11}-\lambda & a& a_{13}& \dots & a_{1m}\\ a_{21}& a_{22}-\lambda & a_{23}& \dots & a_{2m}\\ a_{31}& a_{32}& a_{33}-\lambda & \dots & a_{3m}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& a_{m3}& \dots & a_{mm}-\lambda \end{array}\right|}$

• $p_m\left(\lambda \right)=\det (\lambda 𝑰-𝑨)$, an $m^{\mathrm{th}}$-degree polynomial in $\lambda$, characteristic polynomial of $𝑨$, with $m$ roots, ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_m$, the eigenvalues of $𝑨$

Eigenproblem in matrix form

• $𝑨\in {ℝ}^{m\times m}$, eigenvalue problem $𝑨𝒙=\lambda 𝒙$ ($𝒙\ne 𝟎$) in matrix form:

  ${\displaystyle 𝑨𝑿=𝑿𝚲}$ ${\displaystyle 𝑿=\left[\begin{array}{lll}{𝒙}_1& \dots & {𝒙}_m\end{array}\right],𝚲=\mathrm{diag}({\lambda }_1,\dots ,{\lambda }_m)=\left[\begin{array}{llll}{\lambda }_1& 0& \dots & 0\\ 0& {\lambda }_2& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & {\lambda }_m\end{array}\right].}$

• $𝑿$ is the eigenvector matrix, $𝚲$ is the (diagonal) eigenvalue matrix

• If column vectors of $𝑿$ are linearly independent, then $𝑿$ is invertible

  ${\displaystyle 𝑨=𝑿𝚲{𝑿}^{-1},}$

  the eigendecomposition of $𝑨$ (compare to $𝑨=𝑳𝑼$, $𝑨=𝑸𝑹$)

• Rule “determinant of product = product of determinants” implies

  ${\displaystyle \det (𝑨𝑿)=\det (𝑿𝚲)\Rightarrow \det \left(𝑨\right)=\det \left(𝚲\right)(\mathrm{for}\det \left(X\right)\ne 0).}$

Simple cases

• Eigendecomposition of $𝑰\in {ℝ}^{m\times m}$. Compare $𝑨𝑿=𝑿𝚲$

  ${\displaystyle 𝑰𝑰=𝑰𝑰,𝑨=𝑰,𝑿=𝑰,𝚲=𝑰}$

  to find eigenvalues ${\lambda }_1=1,\dots$, ${\lambda }_m=1$, eigenvectors ${𝒙}_1={𝒆}_1,\dots$, ${𝒙}_m={𝒆}_m$.

• Eigendecomposition of $𝑨=\mathrm{diag}(s_1,s_2,\dots ,s_m)$. Compare $𝑨𝑿=𝑿𝚲$

  ${\displaystyle 𝑨𝑰=𝑰𝑨}$

  to find eigenvalues ${\lambda }_1=s_1,\dots ,{\lambda }_m=s_m$, eigenvectors ${𝒙}_1={𝒆}_1,\dots ,{𝒙}_m={𝒆}_m$.

• Reflection across $x_1$-axis in ${ℝ}^2$

  ${\displaystyle 𝑨=\left[\begin{array}{ll}1& 0\\ 0& -1\end{array}\right]}$

  is a diagonal matrix, ${\lambda }_1=1$, ${\lambda }_2=-1$, ${𝒙}_1={𝒆}_1$, ${𝒙}_2={𝒆}_2$

${ℝ}^3$ rotation matrix eigenvalues

• Rotate by $\theta$ around $x_3$ axis in ${ℝ}^3$

  ${\displaystyle 𝑨=\left[\begin{array}{lll}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\in {ℝ}^{3\times 3},m=3}$

• One direction not change by rotation is ${𝒙}_3={𝒆}_3$ with ${\lambda }_3=1$

• Where are the other two directions?

  • Compute characteristic polynomial $p_3\left(\lambda \right)=\det (\lambda 𝑰-𝑨)$

    ${\displaystyle p_3\left(\lambda \right)=\left|\begin{array}{lll}\lambda -\cos \theta & \sin \theta & 0\\ -\sin \theta & \lambda -\cos \theta & 0\\ 0& 0& \lambda -1\end{array}\right|=(\lambda -1)({\lambda }^2-2\lambda \cos \theta +1)}$

  • One root of $p_3\left(\lambda \right)$ is ${\lambda }_3=1$, as expected.

  • Solve $$${\lambda }^2-2\lambda \cos \theta +1=0$ to find remaining eigenvalues to be complex

    ${\displaystyle {\lambda }_{1,2}=\cos \theta \pm \sqrt{{\cos }^2\theta -1}=\cos \theta \pm i\sin \theta =e^{\pm i\theta }\in ℂ,i^2=-1.}$

Complex numbers primer

• $z\in ℂ$ can be represented in

  • Cartesian form $z=x+iy$

  • Polar form $z=r{e}^{i\theta }=r(\cos \theta +i\sin \theta )$

• Complex conjugate of $z\in ℂ$ negates imaginary part $\bar{z}=x-iy=r{e}^{-i\theta }$

• Absolute value of $z\in ℂ$ is $\left|z\right|={(x^2+y^2)}^{1/2}=r$

• Argument of $z$ is angle $\theta$ from polar form $z=r{e}^{i\theta }$

• Absolute value can be expressed as $\left|z\right|={(\bar{z}z)}^{1/2}$

• Recall for $𝒙\in {ℝ}^m$

  ${\displaystyle {||𝒙||}_2^2={𝒙}^T𝒙=x_1^2+\cdots +x_m^2,}$

  stating that squared 2-norm of real vector $𝒙$ is sum of squares of components.

• Extend above to vector of complex numbers $𝒖\in {ℂ}^m$ by

  ${\displaystyle {||𝒖||}_2^2={\left|u_1\right|}^2+\cdots +{\left|u_m\right|}^2={\left(\overline{𝒖}\right)}^T𝒖.}$

• Taking the complex conjugate and transposing arises frequently, notation

  ${\displaystyle {𝒖}^{\ast }={\left(\overline{𝒖}\right)}^T,\mathrm{adjoint}\mathrm{of}𝒖}$

${ℝ}^3$ rotation matrix eigenvectors

• Consider ${\lambda }_2=e^{i\theta }=\exp (i\theta )=\cos \theta +i\sin \theta$. Eigenvector ${𝒙}_2$ satisfies

  ${\displaystyle (𝑨-{\lambda }_2𝑰){𝒙}_2=𝟎,}$

  which implies ${𝒙}_2\in N(𝑨-{\lambda }_2𝑰)$

• Compute basis vector for $N(𝑨-{\lambda }_2𝑰)$

  ${\displaystyle 𝑨-{\lambda }_2𝑰=\left[\begin{array}{lll}-i\sin \theta & -\sin \theta & 0\\ \sin \theta & -i\sin \theta & 0\\ 0& 0& -e^{i\theta }\end{array}\right]\sim \left[\begin{array}{lll}-i\sin \theta & -\sin \theta & 0\\ 0& 0& 0\\ 0& 0& -e^{i\theta }\end{array}\right].}$

• Find eigenvector

  ${\displaystyle {𝒙}_2=\left[\begin{array}{l}i\\ 1\\ 0\end{array}\right]}$

• Repeat for ${\lambda }_2=e^{-i\theta }$, find ${𝒙}_3=\left[\begin{array}{l}-i\\ 1\\ 0\end{array}\right]$

Verify ${ℝ}^3$ rotation eigenvectors, eigenvalues

• Compute $𝑨{𝒙}_2-{\lambda }_2{𝒙}_2=(𝑨-{\lambda }_2𝑰){𝒙}_2$

  ${\displaystyle (𝑨-{\lambda }_2𝑰){𝒙}_2=\left[\begin{array}{lll}-i\sin \theta & -\sin \theta & 0\\ \sin \theta & -i\sin \theta & 0\\ 0& 0& -e^{i\theta }\end{array}\right]\left[\begin{array}{l}i\\ 1\\ 0\end{array}\right]=\left[\begin{array}{l}0\\ 0\\ 0\end{array}\right]=𝟎.?}$

• In general a polynomial of degree $m$ $p_m\left(\lambda \right)$ with real coefficients has $m$ complext roots ${\lambda }_1,\dots ,{\lambda }_m\in ℂ$

Not all eigenvector matrices are invertible

• Consider

  ${\displaystyle 𝑨=\left[\begin{array}{ll}1& 1\\ 0& 1\end{array}\right]}$

• Eigenvalues ${\lambda }_1={\lambda }_2=1$, a repeated root, since

  ${\displaystyle \det (\lambda 𝑰-𝑨)=\left|\begin{array}{ll}\lambda -1& 1\\ 0& \lambda -1\end{array}\right|={(\lambda -1)}^2.}$

• However

  ${\displaystyle 𝑨-{\lambda }_1𝑰=\left[\begin{array}{ll}0& 1\\ 0& 0\end{array}\right]}$

  $\mathrm{rank}(𝑨-{\lambda }_1𝑰)=1=\dim C\left({(𝑨-{\lambda }_1𝑰)}^T\right)$, FTLA $\Rightarrow \dim N(𝑨-{\lambda }_1𝑰)=1$, only one non-zero eigenvector

Algebraic, geometric multiplicity

Definition 1. The algebraic multiplicity of an eigenvalue $\lambda$ is the number of times it appears as a repeated root of the characteristic polynomial $p\left(\lambda \right)=\det (A-\lambda I)$

Example. $p\left(\lambda \right)=\lambda (\lambda -1){(\lambda -2)}^2$ has two single roots ${\lambda }_1=0$, ${\lambda }_2=1$ and a repeated root ${\lambda }_{3,4}=2$. The eigenvalue $\lambda =2$ has an algebraic multiplicity of 2

Definition 2. The geometric multiplicity of an eigenvalue $\lambda$ is the dimension of the null space of $A-\lambda I$

Definition 3. An eigenvalue for which the geometric multiplicity is less than the algebraic multiplicity is said to be defective

Theorem. A matrix is diagonalizable if the geometric multiplicity of each eigenvalue is equal to the algebraic multiplicity of that eigenvalue.

Computing eigenvectors

• Find eigenvectors as non-trivial solutions of system $(𝑨-\lambda 𝑰)𝒙=0$, e.g., ${\lambda }_1=1$

  ${\displaystyle 𝑨-{\lambda }_1𝑰=\left(\begin{array}{ccc}4& -4& 2\\ 5& -5& 1\\ -2& 2& -4\end{array}\right)\sim \left(\begin{array}{ccc}-2& 2& -4\\ 0& 0& -6\\ 5& -5& 1\end{array}\right)\sim \left(\begin{array}{ccc}-2& 2& -4\\ 0& 0& -6\\ 0& 0& 0\end{array}\right)}$

  Note convenient choice of row operations to reduce amount of arithmetic, and use of knowledge that $𝑨-{\lambda }_1𝑰$ is singular to deduce that last row must be null

• In traditional form the above row-echelon reduced system corresponds to

  ${\displaystyle \{\begin{array}{lll}-2x_1+2x_2-4x_3& =& 0\\ 0x_1+0x_2-6x_3& =& 0\\ 0x_1+0x_2+0x_3& =& 0\end{array}\Rightarrow 𝒙=\alpha \left(\begin{array}{c}1\\ 1\\ 0\end{array}\right),.||𝒙||=1\Rightarrow \alpha =1/\sqrt{2}}$

When is diagonal factorization useful?

• Suppose $𝑨\in {ℝ}^{m\times m}$ diagonalizable, $𝑨=𝑿𝚲{𝑿}^{-1}$

• Repeated application of $𝑨$

  ${\displaystyle {𝑨}^2=(𝑿𝚲{𝑿}^{-1})(𝑿𝚲{𝑿}^{-1})=𝑿{𝚲}^2{𝑿}^{-1}}$ ${\displaystyle {𝑨}^k=(𝑿𝚲{𝑿}^{-1})\cdot \cdots \cdot (𝑿𝚲{𝑿}^{-1})=𝑿{𝚲}^k{𝑿}^{-1}}$

• Above allows definition of $e^{𝑨},\sin \left(𝑨\right),\cos \left(𝑨\right)$, for example

  ${\displaystyle e^x=\frac{1}{0!}{x}^0+\frac{1}{1!}x+\frac{1}{2!}{x}^2+\cdots +\frac{1}{k!}{x}^k+\cdots \Rightarrow }$ ${\displaystyle e^{𝑨}=𝑿(\frac{1}{0!}{𝚲}^0+\frac{1}{1!}𝚲+\frac{1}{2!}{𝚲}^2+\cdots +\frac{1}{k!}{𝚲}^k+\cdots ){𝑿}^{-1}}$

• The differential system ${𝒚}^{\text{'}}=𝑨𝒚$ has solution $𝒚\left(t\right)=e^{𝑨t}y\left(0\right)$.