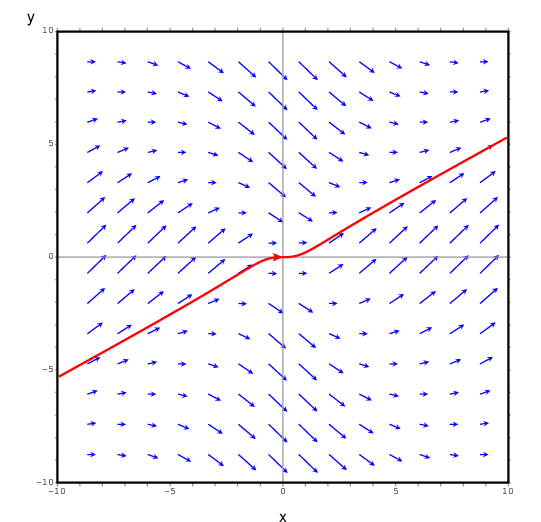
(%i5)
plotdf((x^2-y^2)/(1+x^2+y^2),[trajectory_at,0,0])$
Theorem on existence of solution to IVP
Examples
Theorem. If continuous on the open rectangle , and , then the IVP , has at least one solution on some open interval of that contains
Theorem. If and continuous on the open rectangle , and , then the IVP , has an unique solution on some open interval of that contains
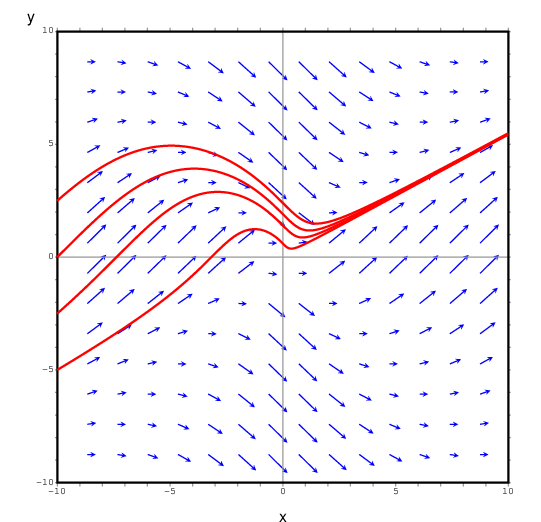
(%i5)
plotdf((x^2-y^2)/(1+x^2+y^2),[trajectory_at,0,0])$

(%i5)
plotdf((x^2-y^2)/(x^2+y^2),[trajectory_at,0,0])$
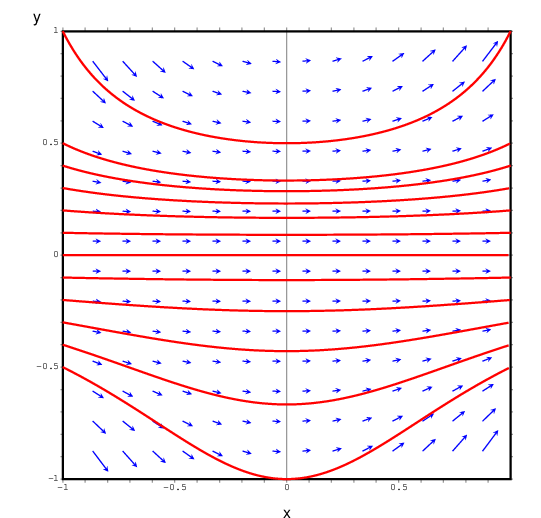
(%i6)
plotdf((x+y)/(x-y),[x,-1,1],[y,-1,1])$

(%i7)
plotdf(2*x*y^2,[x,-1,1],[y,-1,1])$
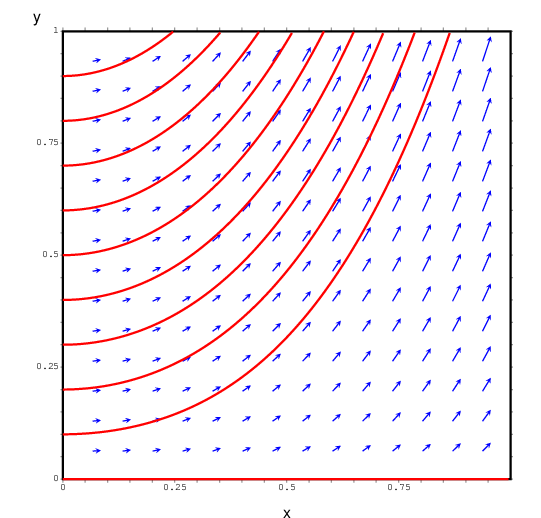
(%i8)
plotdf(10*x*y^.4/3,[x,0,1],[y,0,1])$
(%i9)
plotdf(10*x*y^.4/3,[x,0,1],[y,0,1])$
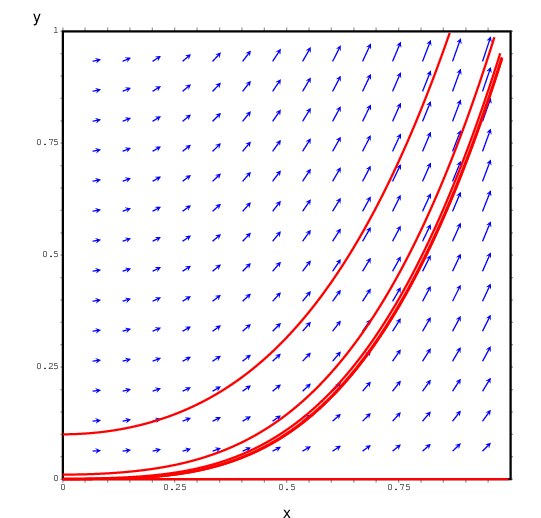
General solution: .
Initial condition: has no solution in .
However in ,