MATH383: A first course in differential equationsFebruary 20, 2019

Solve the following problems (3 course points each). Present a brief motivation of your method of solution. Explicitly state any conditions that must be met for solution procedure to be valid. Organize your computation and writing so the solution you present is readily legible.

No credit is awarded for statement of the final answer to a problem without presentation of the solution procedure.

1. A benefactor wishes to establish a trust fund to pay a researcher's salary for $T$ years. The salary is to start at $S_0$ dollars per year and increase at a fractional rate of $a$ per year. Find the amount of money $P_0$ that the benefactor must deposit in a trust fund paying interest at a rate $r$ per year. Assume that the researcher's salary is paid continuously, the interest is compounded continuously, and the salary increases are granted continuously.

   Solution. The salary increases as $S^{\text{'}}\left(t\right)=aS\left(t\right)$, with solution $S\left(t\right)=e^{at}{S}_0$. The trust fund rate of change is $P^{\text{'}}=rP-S\left(t\right)=rP-e^{at}{S}_0$. Solve homogeneous equation $P^{\text{'}}=rP$ to find $P_h\left(t\right)=u{e}^{rt}$, and apply variation of parameters, ${(u{e}^{rt})}^{\text{'}}=ru{e}^{rt}-e^{at}{S}_0$, to obtain the equation, $u^{\text{'}}=-e^{(a-r)t}{S}_0$, solvable by direct integration to give

   ${\displaystyle u=-\frac{1}{a-r}{e}^{(a-r)t}{S}_0+C,}$

   leading to solution of trust fund balance

   ${\displaystyle P\left(t\right)=C{e}^{rt}-\frac{1}{a-r}{e}^{at}{S}_0.}$

   From initial condition $P\left(0\right)=P_0$ obtain $P_0=C-S_0/(a-r)$, hence

   ${\displaystyle P\left(t\right)=[P_0+\frac{S_0}{a-r}]e^{rt}-\frac{1}{a-r}{e}^{at}{S}_0=P_0{e}^{rt}+\frac{S_0}{a-r}(e^{rt}-e^{at}).}$

   To ensure $P\left(t\right)>0$, i.e., there's always money in the trust fund the initial amount $P_0$ must satisfy

   ${\displaystyle P_0>S_0{\frac{1-e^{(a-r)t}}{r-a}}_{}.}$

   Assuming the trust fund goes to zero balance after $T$ years, $P\left(T\right)=0$

   ${\displaystyle 0=P_0+\frac{S_0}{a-r}(1-e^{(a-r)t})\Rightarrow P_0=\frac{S_0}{r-a}(1-e^{(a-r)t}),}$

   is the necessary initial trust fund amount.

2. A tank initially contains 100 liters of a salt solution with a concentration of .1 g/liter. A solution with a salt concentration of .3 g/liter is added to the tank at 5 liters/min, and the resulting mixture is drained out at the same rate. Find the concentration $K\left(t\right)$ of salt in the tank as a function of time $t$.

   Solution. The tank always contains $V=100$ liters, and the salt in the tank is concentration times volume or $S\left(t\right)=VK\left(t\right)$. With $c=0.3$ g/liter, $Q=5$ liters/minute, the amount of salt added in grams per minute is $cQ$. The amount of salt lost by tank drainage is $QK$, so the change in salt content is

   ${\displaystyle S^{\text{'}}=cQ-QK\Rightarrow V{K}^{\text{'}}=(c-K)Q\Rightarrow K^{\text{'}}+\frac{Q}{V}K=c\frac{Q}{V}.}$

   Solution of homogeneous equation $K^{\text{'}}+(Q/V)K=0$, is $K_h\left(t\right)=e^{-Qt/V}$. BY variation of parameters, try $K\left(t\right)=u\left(t\right)K_h\left(t\right)$, and obtain

   ${\displaystyle u^{\text{'}}=c\frac{Q}{V}{e}^{Qt/V}+C,K\left(t\right)=c\frac{Q}{V}+C{e}^{Qt/V}.}$

   Initial condition $K\left(0\right)=K_0=.1$ g/liter gives $K_0=cQ/V+C\Rightarrow C=K_0-cQ/V$, hence

   ${\displaystyle K\left(t\right)=c\frac{Q}{V}+(K_0-c\frac{Q}{V})e^{Qt/V}=0.3\frac{5}{100}+(0.1-0.3\frac{5}{100})\exp (0.3\frac{5t}{100}).}$

3. Consider the functions $𝑭=\{f_1\left(t\right),f_2\left(t\right),f_3\left(t\right),f_4\left(t\right),f_5\left(t\right)\}=\{1,\cos t,\sin t,\cos 2t,\sin 2t\}$.

   1. Determine whether the functions are linearly independent on the interval $[0,2\pi ]$.

      Solution. Write $a_1{f}_1+a_2{f}_2+a_3{f}_3+a_4{f}_4+a_5{f}_5=0$, with $a_1,\dots ,a_5\in ℝ$,

      ${\displaystyle a_1+a_2\cos t+a_3\sin t+a_4\cos 2t+a_5\sin 2t=0.}$

      Evaluate at $t=-\pi ,-\pi /2,0,\pi /2$ to obtain

      ${\displaystyle \begin{array}{l}{a}_1-a_2+a_4=0\\ a_1-a_3-a_4=0\\ a_1+a_2+a_4=0\\ a_1+a_3-a_4=0\end{array}\Rightarrow \left(\begin{array}{llll}1& -1& 0& 1\\ 1& 0& -1& -1\\ 1& 1& 0& 1\\ 1& 0& 1& -1\end{array}\right)\left(\begin{array}{l}{a}_1\\ a_2\\ a_3\\ a_4\end{array}\right)=\left(\begin{array}{l}0\\ 0\\ 0\\ 0\end{array}\right).}$

      Solve system by Gaussian elimination

      ${\displaystyle \left(\begin{array}{lllll}1& -1& 0& 1& 0\\ 1& 0& -1& -1& 0\\ 1& 1& 0& 1& 0\\ 1& 0& 1& -1& 0\end{array}\right)\sim \left(\begin{array}{lllll}1& -1& 0& 1& 0\\ 0& 2& -1& -3& 0\\ 0& 2& 0& 0& 0\\ 0& 1& 1& -2& 0\end{array}\right)\sim \left(\begin{array}{lllll}1& -1& 0& 1& 0\\ 0& 2& 0& 0& 0\\ 0& 2& -1& -3& 0\\ 0& 1& 1& -2& 0\end{array}\right)\sim \left(\begin{array}{lllll}1& -1& 0& 1& 0\\ 0& 2& 0& 0& 0\\ 0& 0& -1& -3& 0\\ 0& 0& 1& -2& 0\end{array}\right)\sim }$ ${\displaystyle \left(\begin{array}{lllll}1& -1& 0& 1& 0\\ 0& 2& 0& 0& 0\\ 0& 0& -1& -3& 0\\ 0& 0& 0& -5& 0\end{array}\right)}$

      or $a_1=a_2=a_3=a_4=0$. Choose $t=\pi /4$ to then obtain that $a_5=0$, so $𝑭$ forms a linearly independent set.

   2. The functions $f_4,f_5$ can be stated in terms of $f_2,f_3$ through the identities $\sin 2t=2\sin t\cos t$, $\cos 2t={\cos }^{2}t-{\sin }^{2}t$. Does this imply that they are linearly dependent?

      Solution. No, since $\sin 2t=2\sin t\cos t$, $\cos 2t={\cos }^{2}t-{\sin }^{2}t$, are nonlinear relations between $f_1,\dots ,f_5.$, and therefore furnish no information on linear dependence.

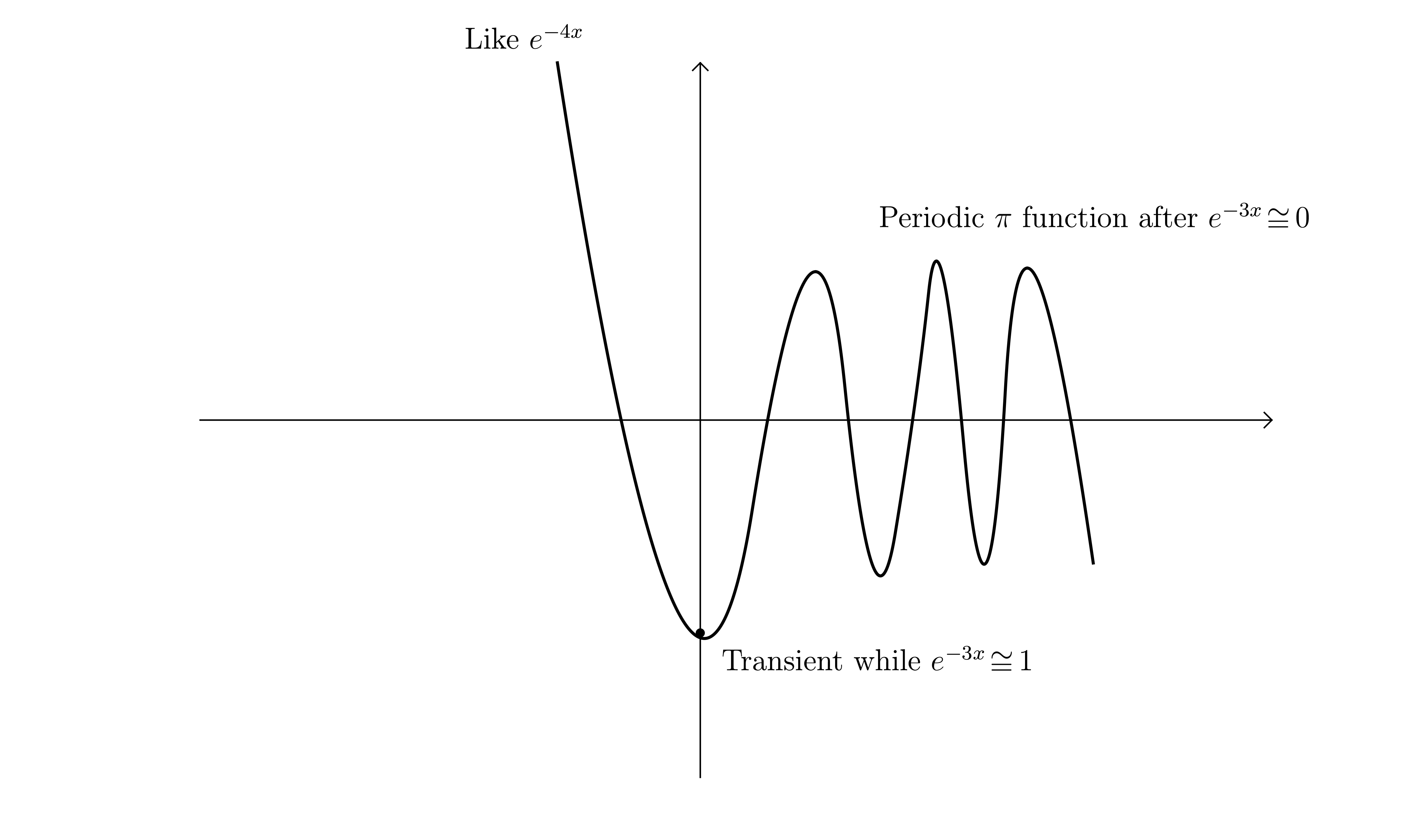
4. Find and subsequently sketch the solution to the initial value problem

   ${\displaystyle y^{\text{'}\text{'}}+7y^{\text{'}}+12y=-2\cos 2x+36\sin 2x,y\left(0\right)=-3,y^{\text{'}}\left(0\right)=2.}$

   Solution. Try $y=e^{rt}$ in the homogeneous equation $y^{\text{'}\text{'}}+7y^{\text{'}}+12y=0$ to find

   ${\displaystyle r^2+7r+12=(r+4)(r+3)=0,}$

   and the homogeneous solution $y_h=c_1{e}^{-3x}+c_2{e}^{-4x}$. Try to find a particular solution of the inhomogeneous equation of the form $y_p=A\sin 2x+B\cos 2x$

   ${\displaystyle {(A\sin 2x+B\cos 2x)}^{\text{'}\text{'}}+7{(A\sin 2x+B\cos 2x)}^{\text{'}}+12(A\sin 2x+B\cos 2x)=-2\cos 2x+36\sin 2x\Rightarrow }$ ${\displaystyle (8A-14B)\sin 2x+(14A+8B)\cos 2x=-2\cos 2x+36\sin 2x\Rightarrow }$ ${\displaystyle \{\begin{array}{l}4A-7B=18\\ 7A+4B=-1\end{array}.\Rightarrow A=1,B=-2.}$

   The solution is

   ${\displaystyle y=\sin 2x-2\cos 2x+c_1{e}^{-3x}+c_2{e}^{-4x}.}$

   Apply initial conditions

   ${\displaystyle \begin{array}{l}y\left(0\right)=-3\Rightarrow -2+c_1+c_2=-3\\ y^{\text{'}}\left(0\right)=2\Rightarrow 2-3c_1-4c_2=2\end{array}\Rightarrow \begin{array}{l}{c}_1+c_2=-1\\ 3c_1+4c_2=0\end{array}\Rightarrow c_1=-4,c_2=3.}$

   Solution is

   ${\displaystyle y=\sin 2x-2\cos 2x-4e^{-3x}+3e^{-4x}.}$