MATH529: Mathematical methods for the physical sciences IIMay 3, 2022

Solve the following problems (4 course points each). Present a brief motivation of your method of solution. No credit awarded for calculations without presentation of solution method. Your objective is to demonstrate mastery of course concepts. Avoid lengthy calculations. Attempt all questions. Questions 1-3 cover material tested on the midterm. The higher of your cummulative score on these three questions or your midterm score is used in grade calculations.

Figure 1. Half-ring $H$, $1<r<e$, $0<\theta <\pi$, $x=r\cos \theta$, $y=r\sin \theta$.

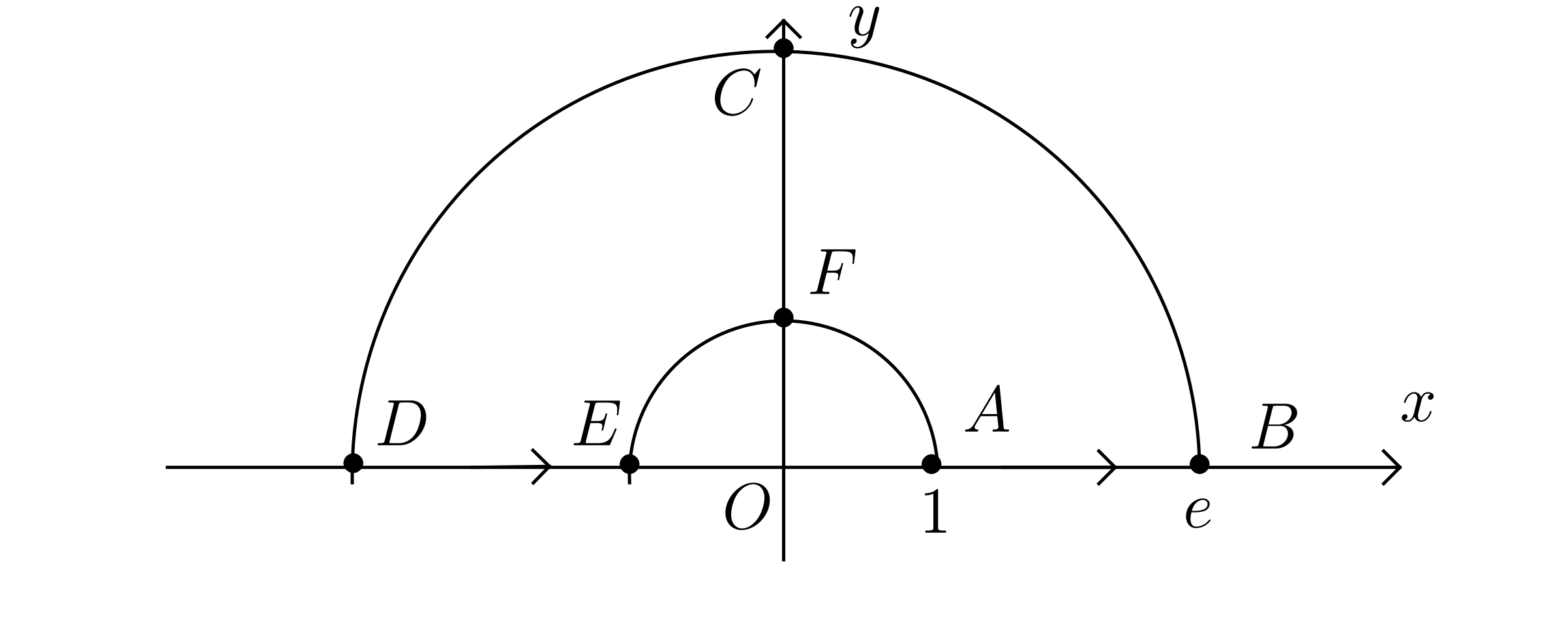
1. Solve ${\nabla }^{2}u=u_{rr}+\frac{1}{r}{u}_r+\frac{1}{r^2}{u}_{\theta \theta }=0$, in the half-ring (Fig. 1), with boundary conditions

   ${\displaystyle \begin{array}{llll}u(r,0)=0& 1<r<e,& u(r,\pi )=0,& 1<r<e,\\ u(1,\theta )=0,& 0<\theta <\pi ,& u(e,\theta )=\sin \theta ,& 0<\theta <\pi .\end{array}}$

2. Find the solution of $u_t={\nabla }^{2}u$ in the half-ring from the initial condition $u=0$.

3. Apply the Laplace transform $ℒ\left\{u(r,\theta ,t)\right\}={\int }_0^{\infty }{e}^{-st}u(r,\theta ,t)dt=U(r,\theta ,s)$ to find the solution of $u_{tt}={\nabla }^{2}u$ in the half-ring from the initial conditions $u=0$, $u_t=\sin \theta$.

4. For $z=x+iy\in ℂ$ prove $\sin z=\sin x\cosh y+i\cos x\sinh y$.

5. Compute the integral

   ${\displaystyle I=\underset{H}{\oint }\frac{}{\sin (z-)}}$

7. Let $w=u+iv=\mathrm{Ln}z=\mathrm{Ln}(x+iy)$, with $\mathrm{Ln}$ denoting the principal value of the complex natural logarithm function. Determine whether $w\left(z\right)$ is a conformal mapping of the half-ring. Sketch the image of the half-ring through $w\left(z\right)$, identifying the images of the points in Fig. 1.

8. Find $\phi (s,t)$, solution of ${\nabla }^2\phi ={\phi }_{ss}+{\phi }_{tt}=0$, with boundary conditions

   ${\displaystyle \begin{array}{llll}\phi (s,0)=0& 0<s<1,& \phi (s,\pi )=0,& 0<s<1,\\ \phi (0,t)=0,& 0<t<\pi ,& \phi (1,t)=\sin t,& 0<t<\pi .\end{array}}$