MATH529

MATH529 L03: Fourier Series

Overview

Orthogonal functions
Fourier Series
Fourier Cosine and Sine Series

Orthogonal functions: inner product

Definition. In $ℝ^{3}$ the inner product $(𝒖, 𝒗)$ of two vectors $𝒖, 𝒗 \in ℝ^{3}$ is defined as

$𝒖 = (\begin{array}{l} u_{1} \\ u_{2} \\ u_{3} \end{array}), 𝒗 = (\begin{array}{l} v_{1} \\ v_{2} \\ v_{3} \end{array}), (𝒖, 𝒗) = u_{1} v_{1} + u_{2} v_{2} + u_{3} v_{3} = \sum_{i = 1}^{3} u_{i} v_{i} \cdot 1$

Definition. In general a scalar product $(,) : 𝒰 \times 𝒰 \to ℝ$ has properties:

$(𝒖, 𝒗) = (𝒗, 𝒖)$

$(k 𝒖 + l 𝒗, 𝒘) = k (𝒖, 𝒘) + l (𝒗, 𝒘)$

$(𝒖, 𝒖) = 0$ if $𝒖 = 𝟎$ , and $(𝒖, 𝒖) > 0$ if $𝒖 \neq 𝟎$

Definition. The inner product of two functions $f, g : [a, b] \to ℝ$ is defined as

$(f, g) = \int_{a}^{b} f (x) g (x) d x$

Orthogonal functions: inner product

Example. The scalar product of $f (x) = x$ , $g (x) = x^{2}$ , $f, g : [- 1, 1] \to ℝ .$

(f, g) = \int_{- 1}^{1} x \cdot x^{2} d x = \frac{1}{4} {. x^{4} |}_{x = - 1}^{x = 1} = 0

In[6]:=

ScProd[f_,g_]:=Integrate[f g,{x,-1,1}];
Table[ScProd[x^l,x^m],{l,1,4},{m,1,4}]

$(\begin{array}{cccc} \frac{2}{3} & 0 & \frac{2}{5} & 0 \\ 0 & \frac{2}{5} & 0 & \frac{2}{7} \\ \frac{2}{5} & 0 & \frac{2}{7} & 0 \\ 0 & \frac{2}{7} & 0 & \frac{2}{9} \end{array})$

Definition. Functions $f, g$ are orthogonal if their scalar product is null, $(f, g) = 0$ .

Definition. Functions ${ϕ_{1}, ϕ_{2}, \dots}$ are an orthogonal set if $\forall i \neq j \Rightarrow (ϕ_{i}, ϕ_{j}) = 0$ .

Orthogonal functions: norm

The $2$ -norm of vector $𝒖 \in ℝ^{n}$ given by inner product $|| 𝒖 || = {(𝒖, 𝒖)}^{1 / 2} .$
Similarly for functions, $|| f || = {(f, f)}^{1 / 2}$

Definition. Functions ${ϕ_{1}, ϕ_{2}, \dots}$ are an orthonormal set if $\forall i \neq j \Rightarrow (ϕ_{i}, ϕ_{j}) = 0,$ and $\forall i, (ϕ_{i}, ϕ_{i}) = 1 .$ Using Kronecker delta $(ϕ_{i}, ϕ_{j}) = δ_{i j}$ .

${\frac{1}{\sqrt{π}} \cdot 1, \frac{1}{\sqrt{π}} \cos x, \frac{1}{\sqrt{π}} \cos 2 x, \dots}$ is an orthogonal set on $[- π, π]$

(\cos m x, \cos n x) = \int_{- π}^{π} (\cos m x) (\cos n x) d x = \frac{1}{2} \int_{- π}^{π} [\cos (m - n) x + \cos (m + n) x] d x = π δ_{m n}

In[2]:=

ScCos[m_,n_]:=Integrate[Cos[m x] Cos[n x],{x,-Pi,Pi}];
Table[ScCos[m,n],{m,1,3},{n,1,3}]

$(\begin{array}{ccc} π & 0 & 0 \\ 0 & π & 0 \\ 0 & 0 & π \end{array})$

Orthogonal functions: weighted scalar product

For $𝒖, 𝒗 \in ℝ^{2}$ , $𝒖 \cdot 𝒗 = u_{1} v_{1} + u_{2} v_{2}$ , $𝒖 = [\begin{array}{l} u_{1} \\ u_{2} \end{array}], 𝒗 = [\begin{array}{l} v_{1} \\ v_{2} \end{array}], 𝒖 \cdot 𝒗 = 𝒖^{T} 𝒗 = 𝒖^{T} 𝑰 𝒗$
The inner product reflects Euclidean geometry, other geometries described by a weighted version of the inner product ${(𝒖, 𝒗)}_{𝑨} = 𝒖^{T} 𝑨 𝒗$ , with $𝑨$ s.p.d
Similarly for functions $f, g : [a, b] \to ℝ$ , weighted scalar products are defined as
$(f, g) = \int_{a}^{b} w (x) f (x) g (x) d x$

Orthogonal functions: Trigonometric (Fourier) series

Find the expansion of $f (x)$ on the set ${ϕ_{1}, ϕ_{2}, ϕ_{3}, \dots}$ , e.g.:
- expansion on the cosines ${1, \cos x, \cos 2 x, \dots}$
- expansion on the sines ${\sin x, \sin 2 x, \dots}$
- expansion on the trigonometric basis ${1, \sin x, \cos x, \sin 2 x, \cos 2 x, \dots}$
  
  that is analogous to the expansion of a vector
  $𝒖 = u_{1} 𝒆_{1} + u_{2} 𝒆_{2} + u_{3} 𝒆_{3}, u_{1} = (𝒖, 𝒆_{1}), u_{2} = (𝒖, 𝒆_{2}), u_{3} = (𝒖, 𝒆_{3})$
Find a trigonometric (Fourier) series for $f : [- π, π] \to ℝ$ , $f (x) = f (x + 2 π)$
$f (x) = A_{0} \cdot 1 + A_{1} \cdot \cos x + B_{1} \cdot \sin x + A_{2} \cdot \cos 2 x + B_{2} \cdot \sin 2 x + \dots$
The coefficients are
$A_{0} = (f, 1), A_{1} = (f, \cos x), B_{1} = (f, \sin x),$
In general for $f : [- p, p] \to ℝ$
$A_{k} = \int_{- p}^{p} f (x) \cos (k x), B_{k} = \int_{- p}^{p} f (x) \sin (k x) .$

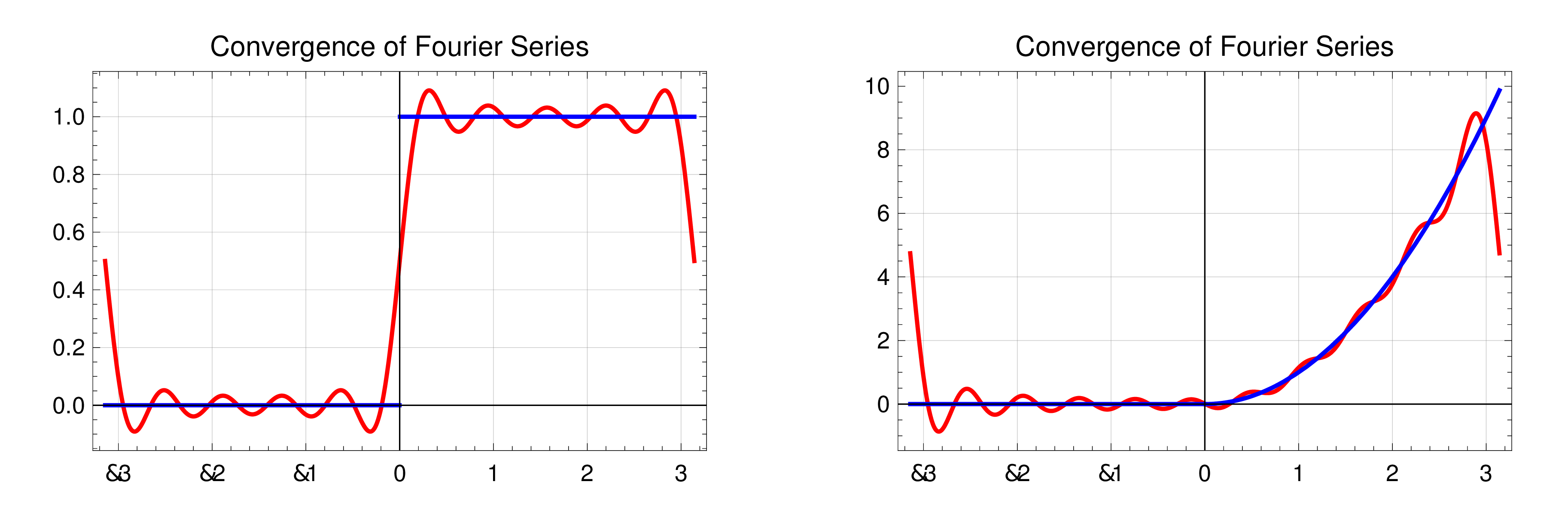
Fourier series convergence

For $f : [- p, p] \to ℝ$ , $f, f^{'}$ piecewise continuous the Fourier series converges to $f (x)$ except at discontinuities where it converges to the arithmetic average
$A_{0} + \sum_{k = 1}^{\infty} (A_{k} \cos [k x] + B_{k} \sin [k x]) \to \frac{1}{2} [f (x_{-}) + f (x_{+})]$

Figure 1. Convergence behavior of Fourier series of discontinuous functions

Cosine series

Consider $f : [- p, p] \to ℝ$ , $f (x) = f (- x)$ , i.e., $f$ is an even function. Then
$f (x) = A_{0} + \sum_{k = 1}^{\infty} A_{k} \cos [k x]$
for $f, f^{'}$ piecewise continuous

Sine series

Consider $f : [- p, p] \to ℝ$ , $f (x) = - f (- x)$ , i.e., $f$ is an odd function. Then
$f (x) = \sum_{k = 1}^{\infty} B_{k} \sin [k x]$
for $f, f^{'}$ piecewise continuous