MATH529: L19 Complex functions

Overview

• Cauchy-Riemann equations

• Exponential and logarithmic functions

• Trigonometric & hyperbolic functions

Cauchy-Riemann conditions

• $w:ℂ\to ℂ$, $w\left(z\right)=u+iv$, $z=x+iy$, $w$ is differentiable at $z_0$ iff

  ${\displaystyle \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}}$

  Proof: $w$ differentiable implies existence of limit ${lim}_{z\to z_0}\frac{w\left(z\right)-w\left(z_0\right)}{z-z_0}=w^{\text{'}}\left(z_0\right)$, irrespective of path $z\to z_0$. Choose two paths $x\to x_0,y=y_0$, $x=x_0$, $y\to y_0$

  ${\displaystyle {lim}_{x\to x_0,y=y_0}\frac{u(x,y_0)-u(x_0,y_0)+i[v(x,y_0)-v(x_0,y_0)]}{x-x_0}=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}}$ ${\displaystyle {lim}_{x=x_0,y\to y_0}\frac{u(x_0,y)-u(x_0,y_0)+i[v(x_0,y)-v(x_0,y_0)]}{i(y-y_0)}=-i\frac{\partial u}{\partial y}+\frac{\partial v}{\partial y}}$

  Identify real and imaginary parts to obtain $\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$

Logarithmic function in $ℂ$

• Defined as inverse of exponential $w=\ln z$, if $z=e^w$

  ${\displaystyle e^w=e^{\ln \left|z\right|+i(\theta +2k\pi )}=e^{\ln \left|z\right|+i\theta }=e^{\ln \left|z\right|}{e}^{i\theta }=e^{\ln \left|z\right|}(\cos \theta +i\sin \theta )}$

• However: $e^w$ periodic, $e^{w+k2\pi i}=e^w$ implies multiple possible values for $\ln z$

  ${\displaystyle \ln z=\ln \left|z\right|+i(\theta +2k\pi )(\ln \left|z\right|={\log }_e\left|z\right|)}$

• Principal value $\mathrm{Ln}z$ in terms of $\mathrm{Arg}z\in (-\pi ,\pi ]$

  ${\displaystyle k\in \mathbb{Z},\mathrm{Ln}z=\log \left|z\right|+i\mathrm{Arg}z}$

• $\mathrm{Ln}z$ analytic in $D=ℂ\backslash (-\infty ,0]$, i.e., the complex plane with a branch cut

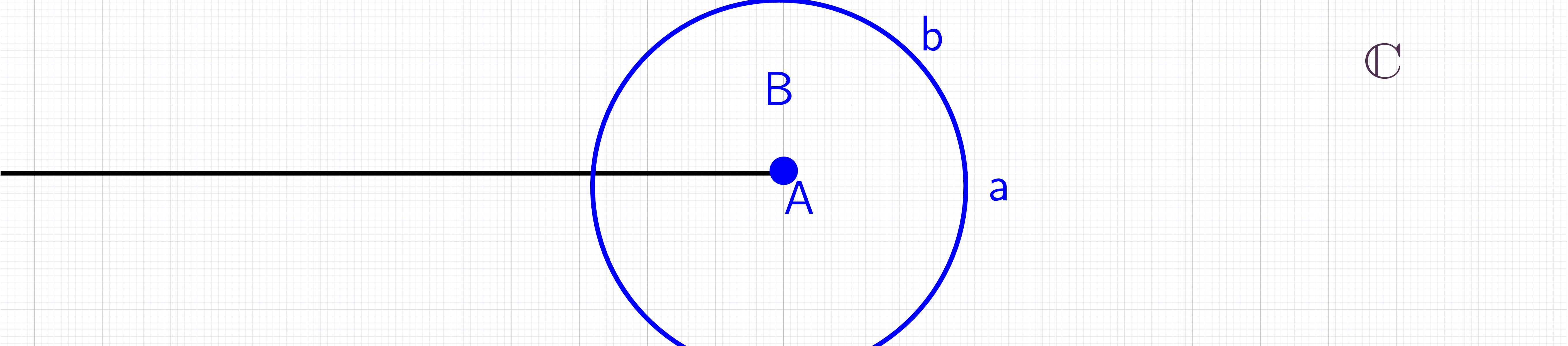
Properties of logarithmic function in $ℂ$

• $\ln (z_1{z}_2)=\ln z_1+\ln z_2$

  ${\displaystyle z_1=r_1{e}^{i{\theta }_1},z_2=r_2{e}^{i{\theta }_2},\ln \left(z_1{z}_2\right)=\ln \left(r_1{r}_2{e}^{i({\theta }_1+{\theta }_2)}\right)=\ln \left(r_1{r}_2\right)+i({\theta }_1+{\theta }_2+2k?\pi )=\ln r_1+\ln r_2+i({\theta }_1+2l\pi )+i({\theta }_2+2m\pi )=\ln z_1+\ln z_2,l+m=k}$

• $\ln (z_1/z_2)=\ln z_1-\ln z_2$

• $\ln z^{\alpha }=\alpha \ln z$

  ${\displaystyle z=r{e}^{i\theta },\ln z^{\alpha }=\ln {(r{e}^{i\theta })}^{\alpha }=\ln r^{\alpha }{e}^{i\alpha \theta }=\ln r^{\alpha }+i(\alpha \theta +2k\pi )=\alpha [\ln r+i(\theta +2k\pi )]=\alpha \ln z}$

• $z^{\alpha }=e^{\alpha \ln z}$

Trigonometric & hyperbolic functions in $ℂ$

• Defined through exponential function

  ${\displaystyle \cos z=\frac{e^{iz}+e^{-iz}}{2}=\cosh (iz),\sin z=\frac{e^{iz}-e^{-iz}}{2i}=-i\sinh (iz)}$ ${\displaystyle iz=e^{i\pi /2}r{e}^{i\theta }=r{e}^{i(\theta +\pi /2)}}$ ${\displaystyle \cosh z=\frac{e^z+e^{-z}}{2}=\cos (iz),\sinh z=\frac{e^z-e^{-z}}{2}=-i\sin (iz)}$

• $\cos z$, $\sin z$, $\cosh z$, $\sinh z$ are entire functions (analytic over $ℂ$)

• Many identities, most remarkable

  ${\displaystyle \sin z=\sin (x+iy)=\sin x\cos (iy)+\cos x\sin (iy)=\sin x\cosh y+i\cos x\sinh y}$ ${\displaystyle \cos z=\cos (x+iy)=\cos x\cos (iy)-\sin \left(x\right)\sin (iy)=\cos x\cosh y-i\sin x\sinh y}$

Inverse trigonometric & hyperbolic functions in $ℂ$

• $w={\sin }^{-1}z=-i\ln [iz+{(1-z^2)}^{1/2}]$ if $z=\sin w$

  ${\displaystyle z=\frac{e^{iw}-e^{-iw}}{2i},t=e^{iw},z=\frac{t^2-1}{2it}\Rightarrow t^2-2izt-1=0}$ ${\displaystyle t_{1,2}=iz\pm \sqrt{-z^2+1},t=iz+\sqrt{1-z^2}=e^{iw}\Rightarrow iw=\ln [iz+\sqrt{1-z^2}]\Rightarrow }$ ${\displaystyle w=-i\ln [iz+\sqrt{1-z^2}]}$

• $w={\cos }^{-1}z=-i\ln [z+{(1-z^2)}^{1/2}]$ if $z=\cos w$

• $w={\sinh }^{-1}z=\ln [z+{(z^2+1)}^{1/2}]$ if $z=\sinh w$

• $w={\cosh }^{-1}z=\ln [z+{(z^2-1)}^{1/2}]$ if $z=\cosh w$