MATH529: L21 $ℂ$ integration

Overview

• Bounding integral values

• Cauchy-Goursat theorem

• Cauchy's integral formulas

Integral bounds

• If $f$ continuous on smooth curve $C$ and $\left|f\left(z\right)\right|⩽M$ for $\forall z\in C$ then

  ${\displaystyle |\underset{C}{\int }f\left(z\right)dz|⩽ML}$

  with $L$ the curve length

• Example

  ${\displaystyle I=\underset{\left|z\right|=4}{\oint }\frac{e^z}{z+1}dz}$ ${\displaystyle |z_1+z_2|⩽\left|z_1\right|+\left|z_2\right|}$ ${\displaystyle \left|z_1\right|⩽|z_1+z_2+(-z_2)|⩽|z_1+z_2|+\left|z_2\right|\Rightarrow \left|z_1\right|-\left|z_2\right|⩽|z_1+z_2|}$ ${\displaystyle \left|\frac{e^z}{z+1}\right|=\frac{\left|e^z\right|}{|z+1|}⩽\frac{\left|e^z\right|}{\left|z\right|-1}=\frac{\left|e^x{e}^{iy}\right|}{\left|z\right|-1}=\frac{\left|e^x\right|}{\left|z\right|-1}⩽\frac{e^4}{3}\Rightarrow I⩽\frac{e^4}{3}2\pi 4=\frac{8\pi e^4}{3}}$

Cauchy-Goursat theorem: Domains

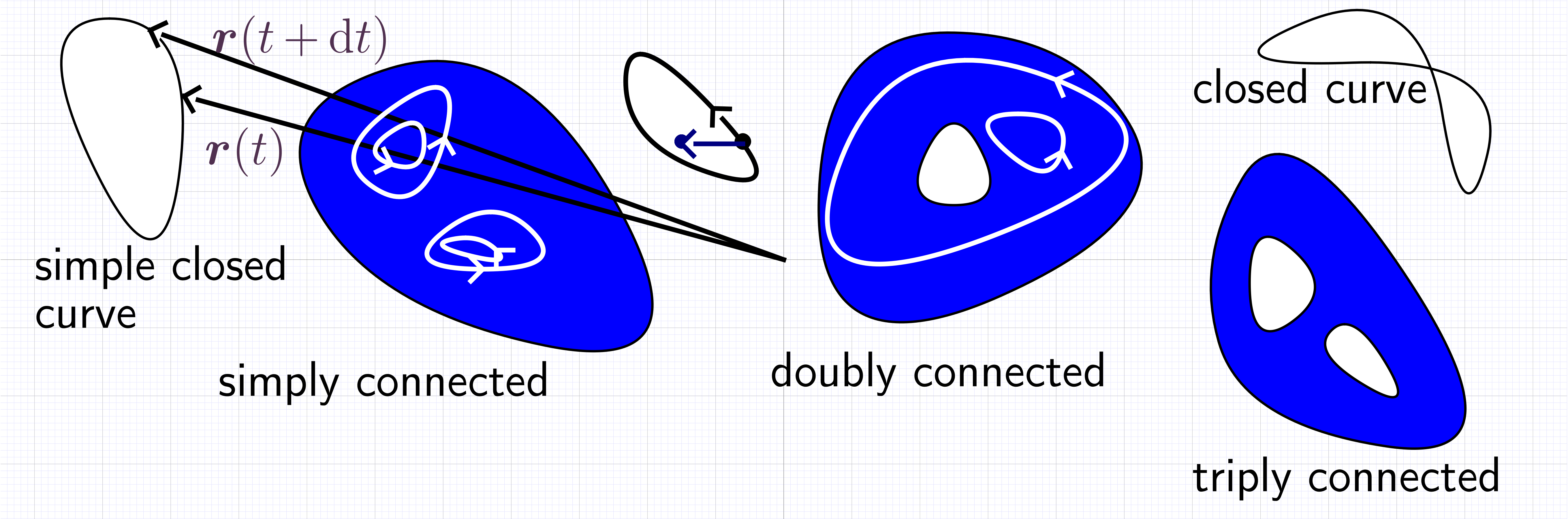
• Consider contour integrals, i.e., integrals over a simple closed curve $C$ $I={\oint }_{C}f\left(z\right)dz$, $𝒓\left(t\right)=x\left(t\right){𝒆}_x+y\left(t\right){𝒆}_y$, $𝝉={𝒓}^{\text{'}}\left(t\right)$, $f:[a,b]\to ℝ$, $f^{\text{'}}:(a,b)\to ℝ$

• Recall: a domain in $ℂ$ is an open and connected set within $ℂ$

  • a domain is simply connected if any contour can be shrunk to a point without leaving the domain (domain has no “holes”)

  • otherwise the domain is multiply connected, e.g., doubly connected, triply connected, etc.

Circulation, flux, Green's theorem

• Closed curve $C:𝒓\left(s\right)$, tangent, normal vectors $𝒕\left(s\right),𝒏\left(s\right)$$$,

  $f:ℂ\to ℂ$, $f=u+iv$, $𝒗=u{𝒆}_x+v{𝒆}_y$, $𝒗:{ℝ}^2\to {ℝ}^2$$$

  • $\Gamma ={\oint }_c𝒗(x\left(s\right),y\left(s\right))\cdot 𝒕\left(s\right)ds$ is the circulation of $𝒗$ on curve $C$.

    ${\displaystyle \underset{c}{\oint }𝒗(x\left(s\right),y\left(s\right))𝒕\left(s\right)ds=\underset{c}{\oint }udx+vdy}$

  • $\Phi ={\oint }_c𝒗(x\left(s\right),y\left(s\right))\cdot 𝒏\left(s\right)ds$ is the flux of $𝒗$ across curve $C$.

    ${\displaystyle \underset{c}{\oint }𝒗(x\left(s\right),y\left(s\right))𝒏\left(s\right)ds=\underset{c}{\oint }udy-vdx}$

  • In $ℂ$: $\Psi =\Gamma +i\Phi ={\oint }_c(u-iv)(dx+idy)={\oint }_c\overline{f\left(z\right)}dz$,

    $\Gamma =\mathrm{Re}\left(\Psi \right)$, $\Phi =\mathrm{Im}\left(\Psi \right)$

• Green's theorem

  ${\displaystyle \underset{C=\partial D}{\oint }pdx+qdy=\underset{D}{iint}(\frac{\partial q}{\partial x}-\frac{\partial p}{\partial y})dA}$

Cauchy theorem

Theorem. If $f$ is analytic in a simply connected domain $D\subseteq ℂ$ and $f^{\text{'}}$ is continuous then $I={\oint }_{C}f\left(z\right)dz=0$ for any contour $C$ within $D$.

Cauchy-Goursat

• Continuity of $f^{\text{'}}$ not required

Theorem. If $f$ is analytic in a simply connected domain $D\subseteq ℂ$ then $I={\oint }_{C}f\left(z\right)dz=0$ for any contour $C$ within $D$.

• ${\oint }_C{e}^{z}dz=0$

• ${\oint }_C{z}^{n}dz=0,n\in \mathbb{N}$

• ${\oint }_{|z-2|=1}{z}^{-2}dz=0$

• ${\oint }_{|z-2|=1}{z}^{-1}dz=0$

• ${\oint }_{\left|z\right|=1}{z}^{-1}dz=2\pi i\ne 0$

Examples

• ${\oint }_{|z-i|=1}\frac{1}{z-i}dz=2\pi i$

• ${\oint }_{|z-2|=2}\frac{5z+7}{z^2+2z-3}dz=6\pi i$

• ${\oint }_{\left|z\right|=3}\frac{1}{z^2+1}dz=0$

Cauchy's integral formulas: for the function

• $f$ analytic in domain $D$, and $C$ a simple closed contour in $D$

  ${\displaystyle f\left(z_0\right)=\frac{1}{2\pi i}\underset{C}{\oint }\frac{f\left(z\right)}{z-z_0}dz}$

  (1)

• Proof: Let $C_{\epsilon }$ be circle of radius $\epsilon$ around $z_0$

  ${\displaystyle \underset{C}{\oint }\frac{f\left(z\right)}{z-z_0}dz=\underset{{}_{C_{\epsilon }}}{\oint }\frac{f\left(z\right)-f\left(z_0\right)+f\left(z_0\right)}{z-z_0}dz=M\epsilon +f\left(z_0\right)\underset{C_{\epsilon }}{\oint }\frac{1}{z-z_0}dz\Rightarrow }$ ${\displaystyle \underset{C}{\oint }\frac{f\left(z\right)}{z-z_0}dz=M\epsilon +f\left(z_0\right)2\pi i,\mathrm{take}\mathrm{limit}\epsilon \to 0\Rightarrow \left(1\right)}$

Cauchy integral formula for derivatives

• $f$ analytic along with derivatives up to order $n$ in domain $D$, and $C$ a simple closed contour in $D$

  ${\displaystyle f^{\left(n\right)}\left(z_0\right)=\frac{n!}{2\pi i}\underset{C}{\oint }\frac{f\left(z\right)}{{(z-z_0)}^{n+1}}dz}$

  (2)

• Examples:

  • ${\oint }_C\frac{z+1}{z^4+4z^3}dz=-\frac{3\pi }{32}i$, $C:\left|z\right|=1$

  • ${\oint }_C\frac{z^3+3}{z{(z-i)}^2}dz=-6\pi i$, $C:$figure “8” enclosing $z_1=0$, $z_2=i$