MATH529: Mathematical methods for the physical sciences IIMarch 6, 2024

Concisely answer the following problems (2 course points each). Present brief motivation of your solutions.

Motivation: How to rapidly shut down a nuclear reactor.

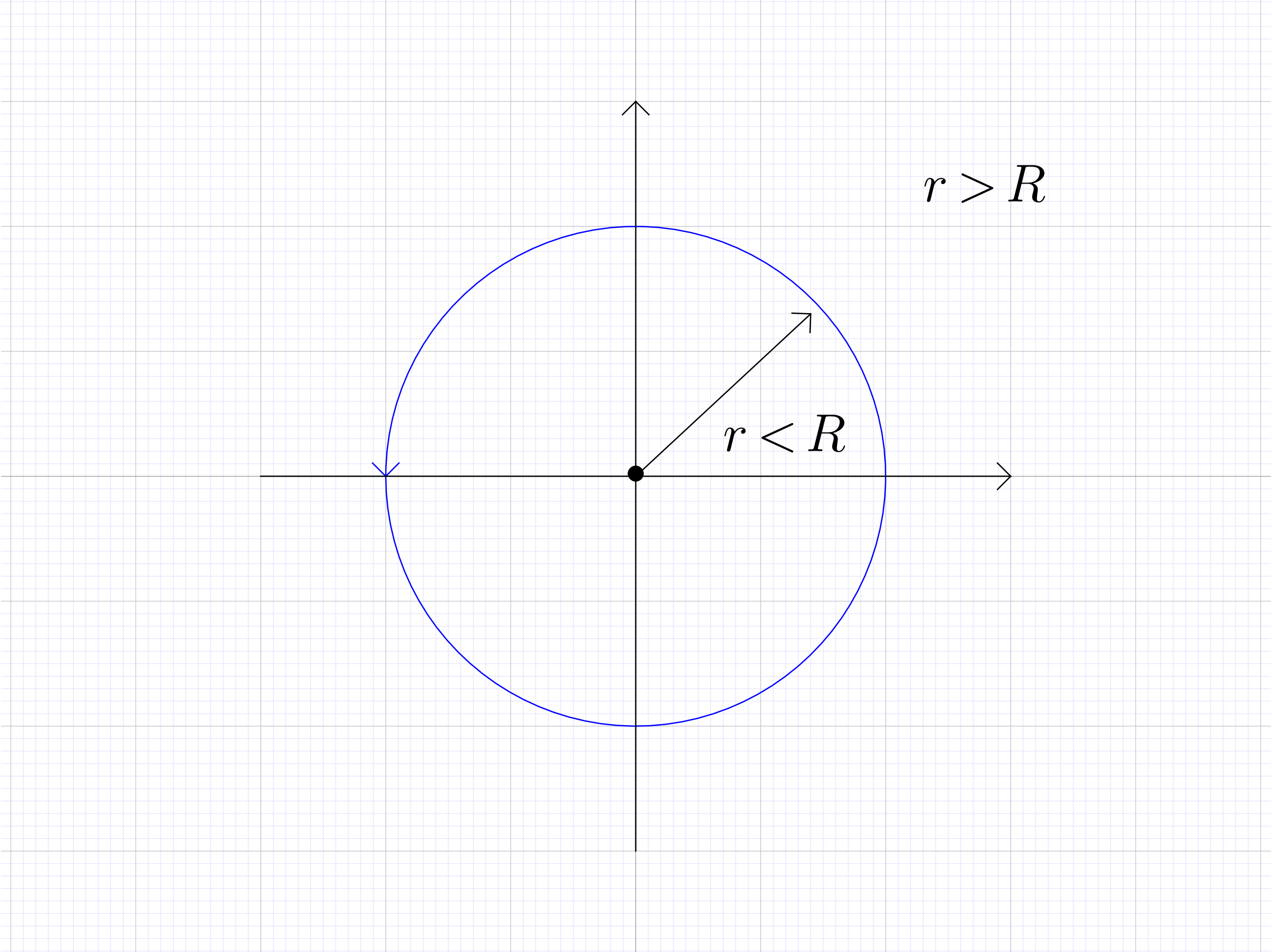
A cylindrical rod of radius $R=0.1$ (m) at initial temperature $u(r<R,0)=U=1000$ (K) is rapidly cooled by quenching, i.e., rapid insertion into a cooling medium of ambient temperature $u(r>R,0)=0$ (K). The cooling medium is much larger than the rod radius, hence is considered to be infinite. The rod is long by comparison to its radius, hence heat conduction is considered only in a cross section.

1. Assuming that heat continuously flows into the rod to maintain its initial temperature, state the IBVP for the temperature distribution $u(r,t)$, $r⩾R$, $t⩾0$ in the cooling medium. Classify the problem you obtain. (Exterior Problem)

2. Assuming that the temperature of the cooling medium is constant, state the IBVP for the temperature distribution $u(r,t)$, $r⩽R$, $t⩾0$ in the rod cross section. Classify the problem you obtain. (Interior Problem)

3. Solve the Exterior Problem.

4. Solve the Interior Problem.

5. Consider the rod to have an initial thermal energy density $Q$ (J/m${}^2$), i.e. amount of heat initially present in a cross section of the rod. When quenched, this initial heat content is distributed throughout the rod and cooling medium. Classify the IBVPs governing this phenomenon. (There is no requirement to actually formulate the IBVPs).

Fundamental physical units: m - meter, s - second, kg - kilogram, K - Kelvin

Derived physical units: J = kg m${}^2$/s - Joule, W=J/s - Watt

Unforced heat equation $u_t=k{\nabla }^{2}u$

Specific heat $c$, $Q=mcu/A$, $m$ mass, $u$ temperature, $A$ cross-section area

Figure 1. Rod thermal quenching