MATH529: Mathematical methods for the physical sciences IIMarch 10, 2022

Solve the following problems (3 course points each). Present a brief motivation of your method of solution.

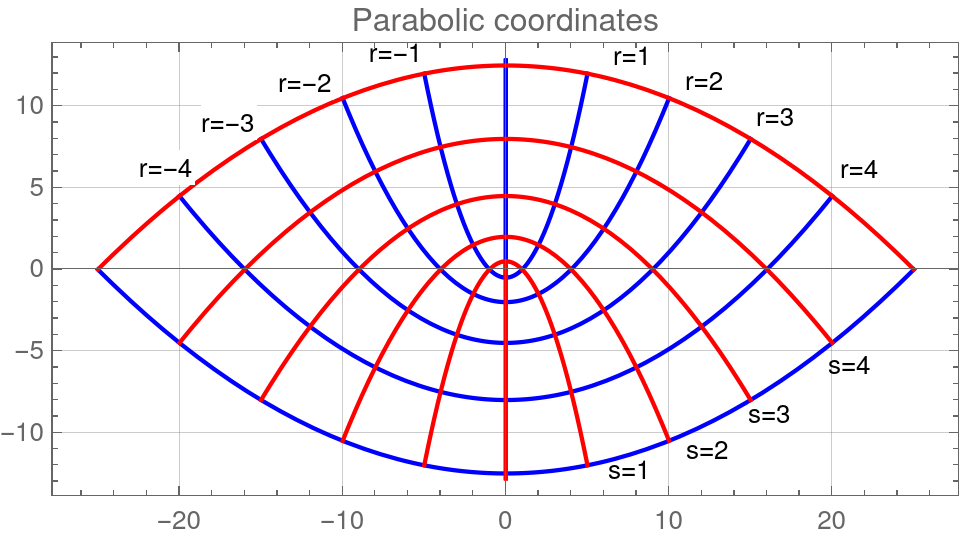
Parabolic coordinates $(a,b)$ are related to rectangular coordinates $(x,y)$ through

have metric coefficients $L_r=L_s=\sqrt{r^2+s^2}$, and the Laplacian

Figure 1. Parabolic coordinate lines of constant $r$ (blue) and constant $s$ (red). Parabolic coordinates are useful in optics and acoustics lens design.

1. Use separation of variables to find the parabolic coordinate solution $u(r,s,t)$ of the initial boundary value problem

   ${\displaystyle \begin{array}{llll}{u}_{tt}=c^2{\nabla }^{2}u,& t>0,& -5<r<5,& -5<s<5,\\ u(r,5,t)=0,& t>0,& -5<r<5,& \\ u(5,s,t)=0,& t>0,& & -5<s<5,\\ u(r,s,0)=f(r,s),& & -5<r<5,& -5<s<5,\\ u_t(r,s,0)=0,& & -5<r<5,& -5<s<5.\end{array}}$

2. Use separation of variables to find the parabolic coordinate solution $u(r,s,t)$ of the initial boundary value problem

   ${\displaystyle \begin{array}{llll}{u}_t=c^2{\nabla }^{2}u,& t>0,& -5<r<5,& -5<s<5,\\ u(r,5,t)=1,& t>0,& -5<r<5,& \\ u(5,s,t)=0,& t>0,& & -5<s<5,\\ u(r,s,0)=0,& & -5<r<5,& -5<s<5.\end{array}}$

3. Find the solution of Problem 1 through the Laplace transform

   ${\displaystyle U(r,s,\tau )=ℒ\left\{u(r,s,t)\right\}=\underset{0}{\overset{\infty }{\int }}u(r,s,t)e^{-t\tau }dt.}$

4. Find the solution of Problem 2 through the Fourier transform

   ${\displaystyle U(a,s,t)=ℱ\left\{u(r,s,t)\right\}=\underset{-\infty }{\overset{\infty }{\int }}u(r,s,t)e^{iar}dr.}$

   Recall the Fourier transform of monomials formula

   ${\displaystyle ℱ\left\{r^n\right\}=\underset{-\infty }{\overset{\infty }{\int }}{r}^n{e}^{-iar}dr=2\pi {(-i)}^n{\delta }^{\left(n\right)}\left(a\right),}$

   where ${\delta }^{\left(n\right)}\left(a\right)$ is the $n^{\mathrm{th}}$ derivative of the Dirac delta function $\delta \left(a\right)$.