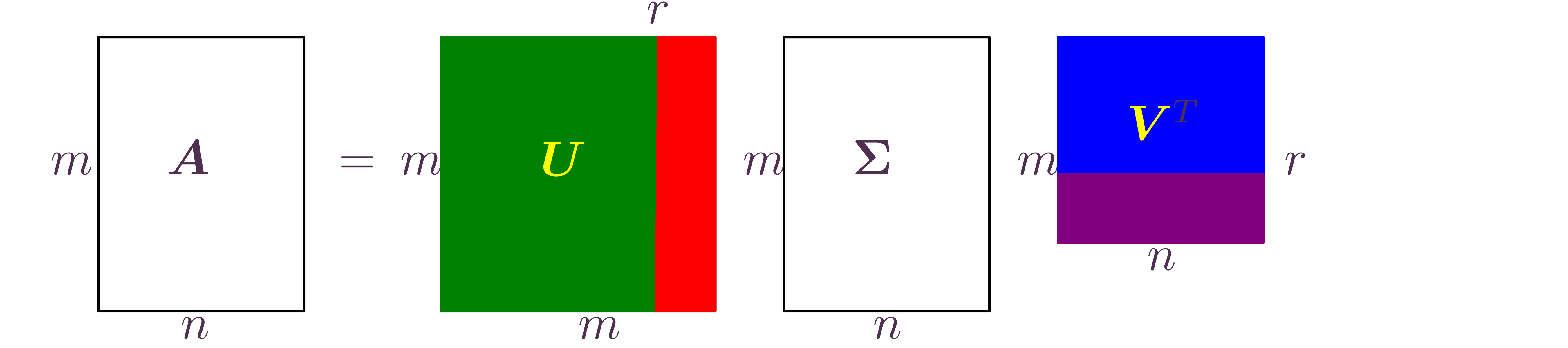"Maymester MATH547 Linear Algebra for Applications in Data Science"

Lesson 12: Course review

What is linear algebra and why is to so important to so many applications?
Basic operations
Factorizations
Fundamental theorem of linear algebra
Exposing the structure of a linear operator between different sets through the SVD
Exposing the structure of a linear operator between the same sets through eigendecomposition

What is linear algebra, and why is it important?

Science acquires and organizes knowledge into theories that can be verified by quantified tests. Mathematics furnishes the appropriate context through rigorous definition of $ℕ, ℝ, ℚ, ℂ$ .
Most areas of science require groups of numbers to describe an observation. To organize knowledge rules on how such groups of numbers may be combined are needed. Mathematics furnishes the concept of a vector space $(𝒮, 𝒱, +)$
1. formal definition of a single number: scalar, $α, β \in 𝒮$
2. formal definition of a group of numbers: vector, $𝒖, 𝒗 \in 𝒱$
3. formal definition of a possible way to combine vectors: $α 𝒖 + β 𝒗$
Algebra is concerned with precise definition of ways to combine mathematical objects, i.e., to organize more complex knowledge as a sequence of operations on simpler objects
Linear algebra concentrates on one particular operation: the linear combination $α 𝒖 + β 𝒗$
It turns out that a complete theory can be built around the linear combination, and this leads to the many applications linear algebra finds in all branches of knowledge.

Basic operations, concepts

Group vectors as column vectors into matrices $𝑨 = (\begin{array}{llll} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}) \in ℝ^{m \times n}$
Define matrix-vector multiplication to express the basic linear combination operation
$𝒃 = 𝑨 𝒙 = x_{1} 𝒂_{1} + \dots + x_{n} 𝒂_{n}$
Introduce a way to switch between column and row storage through the transposition operation $𝑨^{T}$ . ${(𝑨 + 𝑩)}^{T} = 𝑨^{T} + 𝑩^{T}$ , ${(𝑨 𝑩)}^{T} = 𝑩^{T} 𝑨^{T}$
Transform between one set of basis vectors and another $𝒃 𝑰 = 𝑨 𝒙$
Linear independence establishes when a vector cannot be described as a linear combination of other vectors, i.e., if the only way to satisfy $x_{1} 𝒂_{1} + \dots + x_{n} 𝒂_{n} = 𝟎$ is for $x_{1} = \dots = x_{n} = 0$ , then the vectors $𝒂_{1}, \dots, 𝒂_{n}$ are linearly independent
The span $⟨ 𝒂_{1}, \dots, 𝒂_{n} ⟩ = {𝒃 | . \exists 𝒙 \in ℝ^{n} such that 𝒃 = x_{1} 𝒂_{1} + \dots x_{n} 𝒂_{n}}$ is the set of all vectors is reachable by linear combination of $𝒂_{1}, \dots, 𝒂_{n}$
The set of vectors ${𝒂_{1}, \dots, 𝒂_{n}}$ is a basis of a vector space $𝒱$ if $⟨ 𝒂_{1}, \dots, 𝒂_{n} ⟩ = 𝒱$ , and $𝒂_{1}, \dots, 𝒂_{n}$ are linearly independent
The number of vectors in a basis is the dimension of a vector space.

Characterization of a linear operator

Any linear operator $A : 𝒟 \to 𝒞$ , $A (α 𝒖 + β 𝒗) = α A (𝒖) + β A (𝒗)$ can be characterized by a matrix
For each matrix $𝑨 \in ℝ^{m \times n}$ there exist four fundamental subspaces:
1. Column space, $C (𝑨) = {𝒃 \in ℝ^{m} | \exists 𝒙 \in ℝ^{n} such that 𝒃 = 𝑨 𝒙} \subseteq ℝ^{m}$ , the part of $ℝ^{m}$ reachable by linear combination of columns of $𝑨$
2. Left null space, $N (𝑨^{T}) = {𝒚 \in ℝ^{m} | 𝑨^{T} 𝒚 = 0} \subseteq ℝ^{m}$ , the part of $ℝ^{m}$ not reachable by linear combination of columns of $𝑨$
3. Row space, $R (𝑨) = C (𝑨^{T}) = {𝒄 \in ℝ^{n} | \exists 𝒚 \in ℝ^{m} such that 𝒄 = 𝑨^{T} 𝒚} \subseteq ℝ^{n}$ , the part of $ℝ^{m}$ reachable by linear combination of rows of $𝑨$
4. Null space, $N (𝑨) = {𝒙 \in ℝ^{n} | 𝑨 𝒙 = 0} \subseteq ℝ^{n}$ , the part of $ℝ^{m}$ not reachable by linear combination of rows of $𝑨$
The fundamental theorem of linear algebra (FTLA) states
$\begin{array}{rcl} C (𝑨), N (𝑨^{T}) \leq ℝ^{m}, C (𝑨) ⊥ N (𝑨^{T}), & C (𝑨) \cap N (𝑨^{T}) = {𝟎}, & C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m} \\ C (𝑨^{T}), N (𝑨) \leq ℝ^{n}, C (𝑨^{T}) ⊥ N (𝑨), & C (𝑨^{T}) \cap N (𝑨) = {𝟎}, & C (𝑨^{T}) \oplus N (𝑨) = ℝ^{n} \end{array}$

Factorizations

$𝑳 𝑼 = 𝑨$ , (or $𝑳 𝑼 = 𝑷 𝑨$ with $𝑷$ a permuation matrix) Gaussian elimination, solving linear systems. Given $𝑨 \in ℝ^{m \times m}, 𝒃 \in ℝ^{m}$ , $𝒃 \in C (𝑨)$ , find $𝒙 \in ℝ^{m}$ such that $𝑨 𝒙 = 𝒃 = 𝑰 𝒃$ by:
1. Factorize, $𝑳 𝑼 = 𝑷 𝑨$
2. Solve lower triangular system $𝑳 𝒚 = 𝑷 𝒃$ by forward substitution
3. Solve upper triangular system $𝑼 𝒙 = 𝒚$ by backward substitution
$𝑸 𝑹 = 𝑨$ , (or $𝑸 𝑹 = 𝑷 𝑨$ with $𝑷$ a permutation matrix) Gram-Schmidt, solving least squares problem. Given $𝑨 \in ℝ^{m \times n}$ , $𝒃 \in ℝ^{m}$ , $n ⩽ m$ , solve ${min}_{𝒙 \in ℝ^{n}} || 𝒃 - 𝑨 𝒙 ||$ by:
1. Factorize, $𝑸 𝑹 = 𝑷 𝑨$
2. Solve upper triangular system $𝑹 𝒙 = 𝑸^{T} 𝒃$ by forward substitution
$𝑿 𝚲 𝑿^{- 1} = 𝑨$ , eigendecomposition of $𝑨 \in ℝ^{m \times m}$ ( $𝑿$ invertible if $𝑨$ is normal, i.e., $𝑨 𝑨^{T} = 𝑨^{T} 𝑨$ )
$𝑸 𝑻 𝑸^{T} = 𝑨$ , Schur decomposition of $𝑨 \in ℝ^{m \times m}$ , $𝑸$ orthogonal matrix, $𝑻$ triangular matrix, decomposition always exists
$𝑼 𝚺 𝑽^{T} = 𝑨$ , Singular value decomposition of $𝑨 \in ℝ^{m \times n}$ , $𝑼 \in ℝ^{m \times m}, 𝑽 \in ℝ^{n \times n}$ orthogonal matrices, $𝚺 = diag (σ_{1}, σ_{2}, \dots) \in ℝ_{+}^{m \times n}$ , decomposition always exists

SVD

The SVD of $𝑨 \in ℝ^{m \times n}$ reveals: $rank (𝑨)$ , bases for $C (𝑨), N (𝑨^{T}), C (𝑨^{T}), N (𝑨)$

𝑨 = (\begin{array}{cccccc} 𝒖_{1} & \dots & 𝒖_{r} & 𝒖_{r + 1} & \dots & 𝒖_{m} \end{array}) (\begin{array}{ccccc} σ_{1} \\ ⋱ \\ σ_{r} \\ 0 \\ ⋱ \end{array}) (\begin{array}{c} {𝒗_{1}}^{T} \\ ⋮ \\ {𝒗_{r}}^{T} \\ {𝒗_{r + 1}}^{T} \\ ⋮ \\ {𝒗_{n}}^{T} \end{array})