|
This textbook presents the essential concepts from linear algebra of direct utility to analysis of large data sets. The theoretical foundations of the emerging discipline of Data Science are still being defined at present, but linear algebra is certainly one the cornerstones. Traditional presentations of linear algebra reflect its historical roots with a focus on linear systems and determinants, typically of small size. Presentation of the topic often links solutions of linear systems to posible intersections of lines or planes. Such an approach is ill-suited for data science in which the primary interest is in efficient description of large data sets, and automated extraction of regularity from the available data. Neither is the essence of solving a linear system presented as the information-conserving coordinate transformation that it actually represents when the system matrix is of full rank.
The emphasis in linear algebra presentation suggested by data science is quite different. The focus naturally shifts to the essential problem of efficient description of large data sets using a small, typically incomplete set of feature vectors. Linear algebra becomes the study of the basic operation of linear combination and its potential as a descriptor of large data sets. Rather than concentrate on the basis transformation represented by linear system solution, the focus shifts to maximal information compression. Instead of Gaussian elimination, the crucial algorithm becomes the singular value decomposition. The typical operation required is not to solve a linear system, but to construct low-dimensional approximations of the available data through projection and least squares.
Furthermore, computational exercises based on small matrices obscure the vitality and utility of linear algebra in data science of describing objects as disparate and information-rich as images, medical scans or sound recordings. To more faithfully portray the way linear algebra actually gets used in data science, this textbook is packaged with a complete software environment that contains extensive data sets, code snippets to carry out typical analysis, and procedures to transform heterogeneous data sources into standard linear algebra representations. Rather than relegate computational applications to isolated sections, the entire text is interspersed with practical examples using the Octave language, especially suited for linear algebra, and largely compatible with Matlab.
This textbook is drafted and meant to be worked through in TeXmacs, a scientific editing platform that features “live documents” with embedded computational examples constructed in freely available mathematical software systems such as Asymptote, Eukleides, Gnuplot, Maxima, and Octave. The most convenient method to ensure that these various systems work together as intended is to utilize this textbook within the Math@UNC virtual machine. A virtual machine is a program that runs on a physical computer and emulates another computer. Math@UNC is an Arch Linux environment built under VirtualBox, a freely available emulator that runs on Windows, OS X, Linux, and Solaris host computers. The main advantage of the Math@UNC system is pre-configuration of all Arch Linux and mathematical software settings, thus allowing students to learn usage of scientific software and mathematical concepts in a standard environment.
This textbook was developed for an intensive Maymester course that meets in twelve sessions of three hours each. The content organization reflects a desire to present crucial mathematical ideas and practical skills to students from various backgrounds who might be interested in data science. The key concepts required for mathematics students are present: matrix vector spaces, matrix factorizations, linear systems, eigenvalues. For a more general audience, these mathematical topics are also recast as addressing specific aspects of data: expressiveness, redundancy, efficiency, compression, partitioning. More than a simple relabeling, this reinterpretation allows for application of linear algebra operations to data far removed from the physial sciences or engineering. The text and its associated software environment considers data sets from visual art, music, biology, medicine, social sciences.
Vectors and Matrices 11
1.Quantities 11
1.1.Numbers 11
1.2.Quantities described by a single number 14
1.3.Quantities described by multiple numbers 14
2.Vectors 14
2.1.Vector spaces 14
2.2.Real vector space 15
Column vectors. 15
Row vectors. 16
Compatible vectors. 17
2.3.Working with vectors 17
Ranges. 17
Visualization. 18
3.Matrices 19
3.1.Forming matrices 19
3.2.Identity matrix 20
4.Linear combinations 20
4.1.Linear combination as a matrix-vector product 20
Linear combination. 21
Matrix-vector product. 21
4.2.Linear algebra problem examples 21
Linear combinations in . 21
Linear combinations in and . 22
5.Vectors and matrice in data science 23
Linear Mappings 24
1.Functions 24
1.1.Relations 24
Homogeneous relations. 25
1.2.Functions 26
1.3.Linear functionals 27
1.4.Linear mappings 28
2.Measurements 28
2.1.Equivalence classes 28
2.2.Norms 29
2.3.Inner product 31
3.Linear mapping composition 33
3.1.Matrix-matrix product 33
Formal Rules 35
1.Algebraic structures 35
1.1.Typical structures 35
Groups. 35
Rings. 35
Fields. 35
1.2.Vector subspaces 36
2.Vector subspaces of a linear mapping 38
Data Redundancy 41
1.Linear dependence 41
2.Basis and dimension 42
3.Dimension of matrix spaces 42
Data Information 43
1.Partition of linear mapping domain and codomain 43
Data Partitioning 45
1.Mappings as data 45
1.1.Vector spaces of mappings and matrix representations 45
1.2.Measurement of mappings 46
2.The Singular Value Decomposition (SVD) 48
2.1.Orthogonal matrices 48
2.2.Intrinsic basis of a linear mapping 49
2.3.SVD solution of linear algebra problems 51
Change of coordinates. 51
Best 2-norm approximation. 52
The pseudo-inverse. 52
Data Compression 53
1.Projection 53
2.Gram-Schmidt 55
3. solution of linear algebra problems 57
3.1.Transformation of coordinates 57
3.2.General orthogonal bases 58
3.3.Least squares 59
Model Reduction 62
1.Projection of mappings 62
2.Reduced bases 63
2.1.Correlation matrices 63
Correlation coefficient. 63
Patterns in data. 64
Data Transformation 67
1.Gaussian elimination and row echelon reduction 67
2.-factorization 68
2.1.Example for 68
2.2.General case 69
3.Inverse matrix 72
3.1.Gauss-Jordan algorithm 72
4.Determinants 73
4.1.Cross product 77
Data Efficiency 77
1.Krylov bases 77
2.Greedy approximation 78
Data Stability 79
1.The eigenvalue problem 79
2.Computation of the SVD 84
Data Resonance 84
1.Bases induced by eigenmodes 84
Most scientific disciplines introduce an idea of the amount of some entity or property of interest. Furthermore, the amount is usually combined with the concept of a number, an abstraction of the observation that the two sets {Mary, Jane, Tom} and {apple, plum, cherry} seem quite different, but we can match one distinct person to one distinct fruit as in {Maryplum, Janeapple, Tomcherry}. In contrast we cannot do the same matching of distinct persons to a distinct color from the set {red, green}, and one of the colors must be shared between two persons. Formal definition of the concept of a number from the above observations is surprisingly difficult since it would be self-referential due to the apperance of the numbers “one” and “two”. Leaving this aside, the key concept is that of quantity of some property of interest that is expressed through a number. Several types of numbers have been introduced in mathematics to express different types of quantities, and the following will be used throughout this text:
The set of natural numbers, , infinite and countable, ;
The set of integers, , infinite and countable;
The set of rational numbers , infinite and countable;
The set of real numbers, infinite, not countable, can be ordered;
The set of complex numbers, , infinite, not countable, cannot be ordered.
A computer has a finite amount of memory, hence cannot represent all numbers, but rather subsets of the above sets. Furthermore, computers internally use binary numbers composed of binary digits, or bits. Many computer number types are defined for specific purposes, and are often encountered in applications such as image representation or digital data acquisition. Here are the main types.
The number types uint8, uint16, uint32, uint64 represent subsets of the natural numbers (unsigned integers) using 8, 16, 32, 64 bits respectively. An unsigned integer with bits can store a natural number in the range from to . Two arbitrary natural numbers, written as can be added and will give another natural number, . In contrast, addition of computer unsigned integers is only defined within the specific range to .
The number types int8, int16, int32, int64 represent subsets of the integers. One bit is used to store the sign of the number, so the subset of that can be represented is from to
Computers approximate the real numbers through the set of floating point numbers. Floating point numbers that use bits are known as single precision, while those that use are double precision. A floating point number is stored internally as where , are bits within the mantissa of length , and , are bits within the exponent, along with signs for each. The default number type is usually double precision, more concisely referred to double. Common constants such as , are predefined as double, can be truncated to single, and the number of displayed decimal digits is controlled by format. The function disp(x) displays its argument x.
The approximation of the reals by the floats is characterized by: realmax, the largest float, realmin the smallest positive float, and eps known as machine epsilon. Machine epsilon highlights the differences between floating point and real numbers since it is defined as the largest number that satisfies . If of course implies , but floating points exhibit “granularity”, in the sense that over a unit interval there are small steps that are indistinguishable from zero due to the finite number of bits available for a float. Machine epsilon is small, and floating point errors can usually be kept under control. Keep in mind that perfect accuracy is a mathematical abstraction, not encountered in nature. In fields as sociology or psychology 3 digits of accuracy are excellent, in mechanical engineering this might increase to 6 digits, or in electronic engineering to 8 digits. The most precisely known physical constant is the Rydberg constant known to 12 digits. The granularity of double precision expressed by machine epsilon is sufficient to represent natural phenomena.
Within the reals certain operations are undefined such as . Special float constants are defined to handle such situations: Inf is a float meant to represent infinity, and NaN (“not a number”) is meant to represent an undefinable result of an arithmetic operation.
Complex numbers are specified by two reals, in Cartesian form as , or in polar form as , , . The computer type complex is similarly defined from two floats and the additional constant I is defined to represent . Functions are available to obtain the real and imaginary parts within the Cartesian form, or the absolute value and argument of the polar form.
Care should be exercised about the cummulative effect of many floating point errors. For instance, in an “irrational” numerical investigation of Zeno's paradox, one might want to compare the distance traversed by step sizes that are scaled by starting from one to , traversed by step sizes scaled by starting from
In the reals the above two expressions are equal, , but this is not verfied for all when using floating point numbers. Lists of the values , for the two orderings , and , can be generated and summed.
In the above numerical experiment a==b expresses an equality relationship which might evaluate as true denoted by 1, or false denoted by 0.
The above was called an “irrational” investigation since in Zeno's original paradox the scaling factor was 2 rather than , and due to the binary representation used by floats equality always holds.
The above numbers and their computer approximations are sufficient to describe many quantities encountered in applications. Typical examples include:
the position of a point on the unit line segment , approximated by the floating point number , to within machine epsilon precision, ;
the measure of resistance to change of the rate of motion known as mass, , ;
the population of a large community expressed as a float , even though for a community of individuals the population is a natural number, as in “the population of the United States is , i.e., 328.2 million”.
In most disciplines, there is a particular interest in comparison of two quantities, and to facilitate such comparison a common reference is used known as a standard unit. For measurement of a length , the meter is a standard unit, as in the statement , that states that is obtained by taking the standard unit ten times, . The rules for carrying out such comparisons are part of the definition of real and rational numbers. These rules are formalized in the mathematical definition of a field presented in the next chapter. Quantities that obey such rules, i.e., belong to a field, can be used in changes of scale and are called scalars. Not all numbers are scalars in this sense. For instance, the integers would not allow a scaling of 1:2 (halving the scale) even though 1,2 are integers.
Other quantities require more than a single number. The distribution of population in the year 2000 among the alphabetically-ordered South American countries (Argentina, Bolivia,..,Venezuela) requires 12 numbers. These are placed together in a list known in mathematics as a tuple, in this case a 12-tuple , with the population of Argentina, that of Bolivia, and so on. An analogous 12-tuple can be formed from the South American populations in the year 2020, say . Note that it is difficult to ascribe meaning to apparently plausible expressions such as since, for instance, some people in the 2000 population are also in the 2020 population, and would be counted twice.
In contrast to the population 12-tuple example above, combining multiple numbers is well defined in operations such as specifying a position within a three-dimensional Cartesian grid, or determining the resultant of two forces in space. Both of these lead to the consideration of 3-tuples or triples such as the force . When combined with another force the resultant is . If the force is amplified by the scalar and the force is similarly scaled by , the resultant becomes
It is useful to distinguish tuples for which scaling and addition is well defined from simple lists of numbers. In fact, since the essential difference is the behavior with respect to scaling and addition, the focus should be on these operations rather than the elements of the tuple.
The above observations underlie the definition of a
vector space by a set whose elements satisfy
certain scaling and addition properties, denoted all
together by the 4-tuple . The first element of the 4-tuple
is a set whose elements are called vectors. The
second element is a set of scalars, and the third is the
vector addition operation. The last is the scaling
operation, seen as multiplication of a vector by a scalar.
The vector addition and scaling operations must satisfy
rules suggested by positions or forces in three-dimensional
space, which are listed in Table . In particular, a vector
space requires definition of two distinguished elements: the
zero vector , and the identity scalar element .
The definition of a vector space reflects everyday experience with vectors in Euclidean geometry, and it is common to refer to such vectors by descriptions in a Cartesian coordinate system. For example, a position vector within the plane can be referred through the pair of coordinates . This intuitive understanding can be made precise through the definition of a vector space , called the real 2-space. Vectors within are elements of , meaning that a vector is specified through two real numbers, . Addition of two vectors, , is defined by addition of coordinates . Scaling by scalar is defined by . Similarly, consideration of position vectors in three-dimensional space leads to the definition of the , or more generally a real -space , , .
Note however that there is no mention of coordinates in the definition of a vector space as can be seen from the list of properties in Table . The intent of such a definition is to highlight that besides position vectors, many other mathematical objects follow the same rules. As an example, consider the set of all continuous functions , with function addition defined by the sum at each argument , and scaling by defined as . Read this as: “given two continuous functions and , the function is defined by stating that its value for argument is the sum of the two real numbers and ”. Similarly: “given a continuous function , the function is defined by stating that its value for argument is the product of the real numbers and ”. Under such definitions is a vector space, but quite different from . Nonetheless, the fact that both and are vector spaces can be used to obtain insight into the behavior of continuous functions from Euclidean vectors, and vice versa.
Since the real spaces play such an important role in themselves and as a guide to other vector spaces, familiarity with vector operations in is necessary to fully appreciate the utility of linear algebra to a wide range of applications. Following the usage in geometry and physics, the real numbers that specify a vector are called the components of . The one-to-one correspondence between a vector and its components , is by convention taken to define an equality relationship,
with the components arranged vertically and enclosed in square brackets. Given two vectors , and a scalar , vector addition and scaling are defined in by real number addition and multiplication of components
The vector space is defined using the real numbers as the set of scalars, and constructing vectors by grouping together scalars, but this approach can be extended to any set of scalars , leading to the definition of the vector spaces . These will often be referred to as -vector space of scalars, signifying that the set of vectors is .
To aid in visual recognition of vectors, the following notation conventions are introduced:
vectors are denoted by lower-case bold Latin letters: ;
scalars are denoted by normal face Latin or Greek letters: ;
the components of a vector are denoted by the corresponding normal face with subscripts as in equation ();
related sets of vectors are denoted by indexed bold Latin letters: .
In Octave, successive components placed vertically are separated by a semicolon.
The equal sign in mathematics signifies a particular equivalence relationship. In computer systems such as Octave the equal sign has the different meaning of assignment, that is defining the label on the left side of the equal sign to be the expression on the right side. Subsequent invocation of the label returns the assigned object. Components of a vector are obtained by enclosing the index in parantheses.
Instead of the vertical placement or components into one column, the components of could have been placed horizontally in one row , that contains the same data, differently organized. By convention vertical placement of vector components is the preferred organization, and shall denote a column vector henceforth. A transpose operation denoted by a superscript is introduced to relate the two representations
and is the notation used to denote a row vector. In Octave, horizontal placement of successive components in a row is denoted by a space.
Addition of real vectors defines another vector . The components of are the sums of the corresponding components of and , , for . Addition of vectors with different number of components is not defined, and attempting to add such vectors produces an error. Such vectors with different number of components are called incompatible, while vectors with the same number of components are said to be compatible. Scaling of by defines a vector , whose components are , for . Vector addition and scaling in Octave are defined using the and operators.
The vectors used in applications usually have a large number of components, , and it is important to become proficient in their manipulation. Previous examples defined vectors by explicit listing of their components. This is impractical for large , and support is provided for automated generation for often-encountered situations. First, observe that Table mentions one distinguished vector, the zero element that is a member of any vector space . The zero vector of a real vector space is a column vector with components, all of which are zero, and a mathematical convention for specifying this vector is . This notation specifies that transpose of the zero vector is the row vector with zero components, also written through explicit indexing of each component as , for . Keep in mind that the zero vector and the zero scalar are different mathematical objects. The ellipsis symbol in the mathematical notation is transcribed in Octave by the notion of a range, with 1:m denoting all the integers starting from to , organized as a row vector. The notation is extended to allow for strides different from one, and the mathematical ellipsis is denoted as m:-1:1. In general r:s:t denotes the set of numbers with , and real numbers and a natural number, , . If there is no natural number such that , an empty vector with no components is returned.
An efficient, expressive feature of many software systems including Octave is to use ranges as indices to a vector, as shown below for the definition of . Note that the index range i is organized as a row, and a transpose operation must be applied to obtain z as a column vector.
A component-by-component display of a vector becomes increasingly unwieldy as the number of components becomes large. For example, the numbers below seem an inefficient way to describe the sine function.
Indeed, such a piece-by-piece approach is not the way humans organize large amounts of information, preferring to conceptualize the data as some other entity: an image, a sound excerpt, a smell, a taste, a touch, a sense of balance, or relative position. All seven of these human senses will be shown to allow representation by linear algebra concepts, including representation by vectors.
As a first example consider visualization, the process of transforming data into a sight perception. A familiar example is constructing a plot of the graph of a function. Recall that in mathematics the graph of a function relating elements of the domain to those in codomain is a set of ordered pairs . For a commonly encountered function such as , the graph contains an uncountably infinite number of elements, and obviously cannot be explicitly listed. The sine function is continuous, meaning that no matter how small an open interval within the function codomain one considers, there exists an interval in the function domain whose image by the sine function is contained in . In mathematical “” notation this is stated as: . This mathematical notation is concise and precise, but perceptive mainly to the professional mathematician. A more intuitive visualization of continuity is obtained by approximating the graph of a function by a finite set of samples, . Strictly speaking, the sampled graph would indicate jumps interpretable as discontinuities, but when plotting the points human sight perception conveys a sense of continuity for large sample sizes, . For the sine function example, consider sampling the domain with a step size , . To obtain a visual representation of the sampled sine function the Octave plot function can be used to produce a figure that will appear in another window, interactively investigated, and subsequently closed. For large one cannot visually distinguish the points in the graph sample, though this is apparent for smaller sample sizes. This is shown below by displaying a subrange of the sampled points with stride . This example also shows the procedure to save a permanent copy of the displayed figure through the Octave print -deps command that places the currently displayed plot into an Encapsulated Postscript file. The generated figure file can be linked to a document as shown here in Figure , in which both plots render samples of the graph of the sine function, but the one with large is perceived as being continuous.
The real numbers themselves form the vector space , as does any field of scalars, . Juxtaposition of real numbers has been seen to define the new vector space . This process of juxtaposition can be continued to form additional mathematical objects. A matrix is defined as a juxtaposition of compatible vectors. As an example, consider vectors within some vector space . Form a matrix by placing the vectors into a row,
To aid in visual recognition of a matrix, upper-case bold Latin letters will be used to denote matrices. The columns of a matrix will be denoted by the corresponding lower-case bold letter with a subscripted index as in equation (). Note that the number of columns in a matrix can be different from the number of components in each column, as would be the case for matrix from equation () when choosing vectors from, say, the real space , .
Vectors were seen to be useful juxtapositions of scalars that could describe quantities a single scalar could not: a position in space, a force in physics, or a sampled function graph. The crucial utility of matrices is their central role in providing a description of new vectors other then their column vectors, and is suggested by experience with Euclidean spaces.
Consider first , the vector space of real numbers. A position vector on the real axis is specified by a single scalar component, , . Read this to mean that the position is obtained by traveling units from the origin at position vector . Look closely at what is meant by “unit” in this context. Since is a scalar, the mathematical expression has no meaning, as addition of a vector to a scalar has not been defined. Recall that scalars were introduced to capture the concept of scaling of a vector, so in the context of vector spaces they always appear as multiplying some vector. The correct mathematical description is , where is the unit vector . Taking the components leads to , where are the first (and in this case only) components of the vectors. Since , , , one obtains the identity .
Now consider , the vector space of positions in the plane. Repeating the above train of thought leads to the identification of two direction vectors and
Continuing the procees to gives
For arbitrary , the components are now rather than the alphabetically ordered letters common for or . It is then consistent with the adopted notation convention to use to denote the position vector whose components are . The basic idea is the same as in the previous cases: to obtain a position vector scale direction by , by ,, by , and add the resulting vectors.
Juxtaposition of the vectors leads to the formation of a matrix of special utility known as the identity matrix
The identity matrix is an example of a matrix in which the number of column vectors is equal to the number of components in each column vector . Such matrices with equal number of columns and rows are said to be square. Due to entrenched practice an exception to the notation convention is made and the identity matrix is denoted by , but its columns are denoted the indexed bold-face of a different lower-case letter, . If it becomes necessary to explicitly state the number of columns in , the notation is used to denote the identity matrix with columns, each with components.
The expression expresses the idea of scaling vectors within a set and subsequent addition to form a new vector . The matrix groups these vectors together in a single entity, and the scaling factors are the components of the vector . To bring all these concepts together it is natural to consider the notation
as a generalization of the scalar expression . It is clear what the operation should signify: it should capture the vector scaling and subsequent vector addition . A specific meaning is now ascribed to by identifying two definitions to one another.
Repeateadly stating “vector scaling and subsequent vector addition” is unwieldy, so a special term is introduced for some given set of vectors .
Similar to the grouping of unit vectors into the identity matrix , a more concise way of referring to arbitrary vectors from the same vector space is the matrix . Combining these observations leads to the definition of a matrix-vector product.
Consider a simple example that leads to a common linear algebra problem: decomposition of forces in the plane along two directions. Suppose a force is given in terms of components along the Cartesian -axes, , as expressed by the matrix-vector multiplication Note that the same force could be obtained by linear combination of other vectors, for instance the normal and tangential components of the force applied on an inclined plane with angle , , as in Figure . This defines an alternate reference system for the problem. The unit vectors along these directions are
and can be combined into a matrix . The value of the components are the scaling factors and can be combined into a vector . The same force must result irrespective of whether its components are given along the Cartesian axes or the inclined plane directions leading to the equality
Interpret equation () to state that the vector could be obtained either as a linear combination of , , or as a linear combination of the columns of , . Of course the simpler description seems to be for which the components are already known. But this is only due to an arbitrary choice made by a human observer to define the force in terms of horizontal and vertical components. The problem itself suggests that the tangential and normal components are more relevant; for instance a friction force would be evaluated as a scaling of the normal force. The components in this more natural reference system are not known, but can be determined by solving the vector equality , known as a linear system of equations. Procedures to carry this out will be studied in more detail later, but Octave provides an instruction for this common problem, the backslash operator, as in x=A\b.
Linear combinations in a real space can suggest properties or approximations of more complex objects such as continuous functions. Let denote the vector space of continuous functions that are periodic on the interval , . Recall that vector addition is defined by , and scaling by , for , . Familiar functions within this vector space are , with , and these can be recognized to intrinsically represent periodicity on , a role analogous to the normal and tangential directions in the inclined plane example.
Define now another periodic function by repeating the values from the interval on all intervals , for . The function is not given in terms of the “naturally” periodic functions , , but could it thus be expressed? This can be stated as seeking a linear combination as studied in Fourier analysis. The coefficients could be determined from an analytical formula involving calculus operations but we'll seek an approximation using a linear combination of terms
Organize this as a matrix vector product , with
The idea is to sample the column vectors of at the components of the vector , , , . Let , and , denote the so-sampled functions leading to the definition of a vector and a matrix . There are coefficients available to scale the column vectors of , and has components. For it is generally not possible to find such that would exactly equal , but as seen later the condition to be as close as possible to leads to a well defined solution procedure. This is known as a least squares problem and is automatically applied in the Octave x=A\b instruction when the matrix A is not square. As seen in the following numerical experiment and Figure , the approximation is excellent even though the information conveyed by samples of is now much more efficiently stored in the form chosen for the columns of and the scaling coefficients that are the components of .
The above examples highlight some essential aspects of linear algebra in the context of data science applications.
Vectors organize information that cannot be expressed as a single number and for which there exists a concept of scaling and addition.
Matrices group together multiple vectors.
The matrix-vector product expresses a linear combination of the column vectors of the matrix.
Solving a linear system , to find for given , re-expresses the linear combination
as another linear combination
For certain problems the linear combination might be more insightful, but the above transformation is information-preserving, with both having the same number of components.
Finding the best approximation of some given by a linear combination of the column vectors of is known as a least squares problem and transforms the information from the components of into components of , and knowledge of the form of the column vectors. If and the form of the columns of can be succintly stated, the transformation compresses information.
Data science seeks to extract regularity directly from available data, not necessarily invoking any additional hypotheses. The typical scenario is that immense amounts of data are available, with limited capability of human analysis. In this context it is apparent that the least squares problem is of greater interest than solving a linear system with a square matrix. It should also be clear that while computation by hand of small examples is useful to solidify theroretical concepts, it is essential to become proficient in the use of software that can deal with large data sets, such as Octave.
The previous chapter focused on mathematical expression of the concept of quantification, the act of associating human observation with measurements, as a first step of scientific inquiry. Consideration of different types of quantities led to various types of numbers, vectors as groupings of numbers, and matrices as groupings of vectors. Symbols were introduced for these quantities along with some intial rules for manipulating such objects, laying the foundation for an algebra of vectors and matrices. Science seeks to not only observe, but to also explain, which now leads to additional operations for working with vectors and matrices that will define the framework of linear algebra.
Explanations within scientific inquiry are formulated as hypotheses, from which predictions are derived and tested. A widely applied mathematical transcription of this process is to organize hypotheses and predictions as two sets and , and then construct another set of all of the instances in which an element of is associated with an element in . The set of all possible instances of and , is the Cartesian product of with , denoted as , a construct already encountered in the definition of the real 2-space where . Typically, not all possible tuples are relevant leading to the following definition.
Similar to the difficulties encountered in attempting rigorous definition of a natural number, careful parsing of the above definition also would reveal self-references since the member of symbol , and the subset of symbol are both themselves examples of relations. As before, this is set aside to concetrate on the key concept of associating an input with an output . Associating an output to an input is also useful, leading to the definition of an inverse relation as , . Note that an inverse exists for any relation, and the inverse of an inverse is the original relation, . From the above, a relation is a triplet (a tuple with three elements), , that will often be referred to by just its last member .
Computers can be programmed to work not only with numbers as Octave does, but also with general symbols as exemplified by another freely available software package called Maxima. Most data science applications involve numerical computation, but some knowledge of symbolic computation is also useful, as when working with sets that often arises in data classification. The colon symbol denotes assignment in Maxima, and sets can be defined using curly braces with automatic elimination of repeated elements. All common set manipulations are provided, such as the Cartesian product , and element of . operations.
Associate the first three Latin and Greek letters by defining . This is a relation between and since it is a subset of , which can be checked by defining a function that checks whether some is also an element of . Maxima functions are defined using the :=operator, and map applies a function to all elements of a set.
Suppose that the Greek alphabet ordering is not known, and might conceivably be associated to any of . This defines another relation . Finally consider possible reorderings of the Greek alphabet, formulated as relationships between and itself, with and two such possible reorderings. The relations defined here will be used to exemplify various properties below.
Many types of relations are defined in mathematics and encountered in linear algebra, and establishing properties of specific relations is an important task within data science. A commonly encountered type of relationship is from a set onto itself, known as a homogeneous relation. Among the above-defined relations are homogeneous, while are not. For homogeneous relations , it is common to replace the set membership notation to state that is in relationship with , with a binary operator notation . Familiar examples include the equality and less than relationships between reals, , in which is replaced by , and is replaced by . The equality relationship is its own inverse, and the inverse of the less than relationship is the greater than relation , , . Homogeneous relations are classified according to the following criteria.
Relation is reflexive if for any . The equality relation is reflexive, , the less than relation is not, .
Relation is symmetric if implies that , . The equality relation is symmetric, , the less than relation is not, .
Relation is anti-symmetric if for , then . The less than relation is antisymmetric, .
Relation is transitive if and implies . for any . The equality relation is transitive, , as is the less than relation , .
Certain combinations of properties often arise. A homogeneous relation that is reflexive, symmetric, and transitive is said to be an equivalence relation. Equivalence relations include equality among the reals, or congruence among triangles. A homogeneous relation that is reflexive, anti-symmetric and transitive is a partial order relation, such as the less than or equal relation between reals. Finally, a homogeneous relation that is anti-symmetric and transitive is an order relation, such as the less than relation between reals.
Functions between sets and are a specific type of relationship that often arise in science. For a given input , theories that predict a single possible output are of particular scientific interest.
The above intuitive definition can be transcribed in precise mathematical terms as is a function if and implies . Since it's a particular kind of relation, a function is a triplet of sets , but with a special, common notation to denote the triplet by , with and the property that . The set is the domain and the set is the codomain of the function . The value from the domain is the argument of the function associated with the function value . The function value is said to be returned by evaluation . The previously defined relations are functions but is not. All relations can be inverted, and inversion of a function defines a new relation, but which might not itself be a function. For example the relation is a function, but its inverse is not.
Familiar functions include:
the trigonometric functions , that for argument return the function values giving the Cartesian coordinates of a point on the unit circle at angular extent from the -axis;
the exponential and logarithm functions , , as well as power and logarithm functions in some other base ;
polynomial functions , defined by a succession of additions and multiplications
Simple functions such as sin, cos, exp, log, are predefined in Octave, and when given a vector argument return the function applied to each vector component.
As seen previously, a Euclidean space can be used to suggest properties of more complex spaces such as the vector space of continuous functions . A construct that will be often used is to interpret a vector within as a function, since with components also defines a function , with values . As the number of components grows the function can provide better approximations of some continuous function through the function values at distinct sample points .
The above function examples are all defined on a domain of scalars or naturals and returned scalar values. Within linear algebra the particular interest is on functions defined on sets of vectors from some vector space that return either scalars , or vectors from some other vector space , . The codomain of a vector-valued function might be the same set of vectors as its domain, . The fundamental operation within linear algebra is the linear combination with , . A key aspect is to characterize how a function behaves when given a linear combination as its argument, for instance or
Consider first the case of a function defined on a set of vectors that returns a scalar value. These can be interpreted as labels attached to a vector, and are very often encountered in applications from natural phenomena or data analysis.
Many different functionals may be defined on a vector space , and an insightful alternative description is provided by considering the set of all linear functionals, that will be denoted as . These can be organized into another vector space with vector addition of linear functionals and scaling by defined by
As is often the case, the above abstract definition can better be understood by reference to the familiar case of Euclidean space. Consider , the set of vectors in the plane with the position vector from the origin to point in the plane with coordinates . One functional from the dual space is , i.e., taking the second coordinate of the position vector. The linearity property is readily verified. For , ,
Given some constant value , the curves within the plane defined by are called the contour lines or level sets of . Several contour lines and position vectors are shown in Figure . The utility of functionals and dual spaces can be shown by considering a simple example from physics. Assume that is the height above ground level and a vector is the displacement of a body of mass in a gravitational field. The mechanical work done to lift the body from ground level to height is with the gravitational acceleration. The mechanical work is the same for all displacements that satisfy the equation . The work expressed in units can be interpreted as the number of contour lines intersected by the displacement vector . This concept of duality between vectors and scalar-valued functionals arises throughout mathematics, the physical and social sciences and in data science. The term “duality” itself comes from geometry. A point in with coordinates can be defined either as the end-point of the position vector , or as the intersection of the contour lines of two funtionals and . Either geometric description works equally well in specifying the position of , so it might seem redundant to have two such procedures. It turns out though that many quantities of interest in applications can be defined through use of both descriptions, as shown in the computation of mechanical work in a gravitational field.
Consider now functions from vector space to another vector space . As before, the action of such functions on linear combinations is of special interest.
The image of a linear combination through a linear mapping is another linear combination , and linear mappings are said to preserve the structure of a vector space, and called homomorphisms in mathematics. The codomain of a linear mapping might be the same as the domain in which case the mapping is said to be an endomorphism.
Matrix-vector multiplication has been introduced as a concise way to specify a linear combination
with the columns of the matrix, . This is a linear mapping between the real spaces , , , and indeed any linear mapping between real spaces can be given as a matrix-vector product.
Vectors within the real space can be completely specified by real numbers, even though is large in many realistic applications. A vector within , i.e., a continuous function defined on the reals, cannot be so specified since it would require an infinite, non-countable listing of function values. In either case, the task of describing the elements of a vector space by simpler means arises. Within data science this leads to classification problems in accordance with some relevant criteria.
Many classification criteria are scalars, defined as a scalar-valued function on a vector space, . The most common criteria are inspired by experience with Euclidean space. In a Euclidean-Cartesian model of the geometry of a plane , a point is arbitrarily chosen to correspond to the zero vector , along with two preferred vectors grouped together into the identity matrix . The position of a point with respect to is given by the linear combination
Several possible classifications of points in the plane are depicted in Figure : lines, squares, circles. Intuitively, each choice separates the plane into subsets, and a given point in the plane belongs to just one in the chosen family of subsets. A more precise characterization is given by the concept of a partition of a set.
In precise mathematical terms, a partition of set is such that , for which . Since there is only one set ( signifies “exists and is unique”) to which some given belongs, the subsets of the partition are disjoint, . The subsets are labeled by within some index set . The index set might be a subset of the naturals, in which case the partition is countable, possibly finite. The partitions of the plane suggested by Figure are however indexed by a real-valued label, with .
A technique which is often used to generate a partition of a vector space is to define an equivalence relation between vectors, . For some element , the equivalence class of is defined as all vectors that are equivalent to , . The set of equivalence classes of is called the quotient set and denoted as , and the quotient set is a partition of . Figure depicts four different partitions of the plane. These can be interpreted geometrically, such as parallel lines or distance from the origin. With wider implications for linear algebra, the partitions can also be given in terms of classification criteria specified by functions.
The partition of by circles from Figure is familiar; the equivalence classes are sets of points whose position vector has the same size, , or is at the same distance from the origin. Note that familiarity with Euclidean geometry should not obscure the fact that some other concept of distance might be induced by the data. A simple example is statement of walking distance in terms of city blocks, in which the distance from a starting point to an address blocks east and blocks north is city blocks, not the Euclidean distance since one cannot walk through the buildings occupying a city block.
The above observations lead to the mathematical concept of a norm as a tool to evaluate vector magnitude. Recall that a vector space is specified by two sets and two operations, , and the behavior of a norm with respect to each of these components must be defined. The desired behavior includes the following properties and formal definition.
The magnitude of a vector should be a unique scalar, requiring the definition of a function. The scalar could have irrational values and should allow ordering of vectors by size, so the function should be from to , . On the real line the point at coordinate is at distance from the origin, and to mimic this usage the norm of is denoted as , leading to the definition of a function , .
Provision must be made for the only distinguished element of , the null vector . It is natural to associate the null vector with the null scalar element, . A crucial additional property is also imposed namely that the null vector is the only vector whose norm is zero, . From knowledge of a single scalar value, an entire vector can be determined. This property arises at key junctures in linear algebra, notably in providing a link to another branch of mathematics known as analysis, and is needed to establish the fundamental theorem of linear algbera or the singular value decomposition encountered later.
Transfer of the scaling operation property leads to imposing . This property ensures commensurability of vectors, meaning that the magnitude of vector can be expressed as a multiple of some standard vector magnitude .
Position vectors from the origin to coordinates on the real line can be added and . If however the position vectors point in different directions, , , then . For a general vector space the analogous property is known as the triangle inequality, for .
Note that the norm is a functional, but the triangle inequality implies that it is not generally a linear functional. Returning to Figure , consider the functions defined for through values
Sets of constant value of the above functions are also equivalence classes induced by the equivalence relations for .
, ;
, ;
, ;
, .
These equivalence classes correspond to the vertical lines, horizontal lines, squares, and circles of Figure . Not all of the functions are norms since is zero for the non-null vector , and is zero for the non-null vector . The functions and are indeed norms, and specific cases of the following general norm.
Denote by the largest component in absolute value of . As increases, becomes dominant with respect to all other terms in the sum suggesting the definition of an inf-norm by
This also works for vectors with equal components, since the fact that the number of components is finite while can be used as exemplified for , by , with .
Note that the Euclidean norm corresponds to , and is often called the -norm. The analogy between vectors and functions can be exploited to also define a -norm for , the vector space of continuous functions defined on .
The integration operation can be intuitively interpreted as the value of the sum from equation () for very large and very closely spaced evaluation points of the function , for instance . An inf-norm can also be define for continuous functions by
where sup, the supremum operation can be intuitively understood as the generalization of the max operation over the countable set to the uncountable set .
Vector norms arise very often in applications, especially in data science since they can be used to classify data, and are implemented in software systems such as Octave in which the norm function with a single argument computes the most commonly encountered norm, the -norm. If a second argument is specified the -norm is computed.
Norms are functionals that define what is meant by the size of a vector, but are not linear. Even in the simplest case of the real line, the linearity relation is not verified for , . Nor do norms characterize the familiar geometric concept of orientation of a vector. A particularly important orientation from Euclidean geometry is orthogonality between two vectors. Another function is required, but before a formal definition some intuitive understanding is sought by considering vectors and functionals in the plane, as depicted in Figure . Consider a position vector and the previously-encountered linear functionals
The component of the vector can be thought of as the number of level sets of times it crosses; similarly for the component. A convenient labeling of level sets is by their normal vectors. The level sets of have normal , and those of have normal vector . Both of these can be thought of as matrices with two columns, each containing a single component. The products of these matrices with the vector gives the value of the functionals
In general, any linear functional defined on the real space can be labeled by a vector
and evaluated through the matrix-vector product . This suggests the definition of another function ,
The function is called an inner product, has two vector arguments from which a matrix-vector product is formed and returns a scalar value, hence is also called a scalar product. The definition from an Euclidean space can be extended to general vector spaces. For now, consider the field of scalars to be the reals .
The inner product returns the number of level sets of the functional labeled by crossed by the vector , and this interpretation underlies many applications in the sciences as in the gravitational field example above. Inner products also provide a procedure to evaluate geometrical quantities and relationships.
In the number of level sets of the functional labeled by crossed by itself is identical to the square of the 2-norm
In general, the square root of satisfies the properties of a norm, and is called the norm induced by an inner product
A real space together with the scalar product and induced norm defines an Euclidean vector space .
In the point specified by polar coordinates has the Cartesian coordinates , , and position vector . The inner product
is seen to contain information on the relative orientation of with respect to . In general, the angle between two vectors with any vector space with a scalar product can be defined by
which becomes
in a Euclidean space, .
In two vectors are orthogonal if the angle between them is such that , and this can be extended to an arbitrary vector space with a scalar product by stating that are orthogonal if . In vectors are orthogonal if .
From two functions and , a composite function, , is defined by
Consider linear mappings between Euclidean spaces , . Recall that linear mappings between Euclidean spaces are expressed as matrix vector multiplication
The composite function is , defined by
Note that the intemediate vector is subsequently multiplied by the matrix . The composite function is itself a linear mapping
so it also can be expressed a matrix-vector multiplication
Using the above, is defined as the product of matrix with matrix
The columns of can be determined from those of by considering the action of on the the column vectors of the identity matrix . First, note that
The above can be repeated for the matrix giving
Combining the above equations leads to , or
From the above the matrix-matrix product is seen to simply be a grouping of all the products of with the column vectors of ,
Matrix-vector and matrix-matrix products are implemented in Octave, the above results can readily be verified.
A vector space has been introduced as a 4-tuple with specific behavior of the vector addition and scaling operations. Arithmetic operations between scalars were implicitly assumed to be similar to those of the real numbers, but also must be specified to obtain a complete definition of a vector space. Algebra defines various structures that specify the behavior operations with objects. Knowledge of these structures is useful not only in linear algebra, but also in other mathematical approaches to data analysis such as topology or geometry.
A group is a 2-tuple containing a set and an operation with
properties from Table . If , , the group is said to be
commutative. Besides the familiar example of integers under
addition , symmetry groups that specify spatial or functional
relations are of particular interest. The rotations by or
vertices of a square form a group.
A ring is a 3-tuple containing a set and two operations
with properties from Table . As is often the case, a ring is
more complex structure built up from simpler algebraic
structures. With respect to addition a ring has the properties
of a commutative group. Only associativity and existence of an
identity element is imposed for multiplication. Matrix
addition and multiplication has the structure of ring
A ring is a 3-tuple containing a set and two operations ,
each with properties of a commutative group, but with special
behavior for the inverse of the null element. The
multiplicative inverse is denoted as . Scalars in the
definition of a vector space must satisfy the properties of a
field. Since the operations are often understood from context
a field might be referred to as the full , or, more concisely
just through the set of elements as in the definition of a
vector space.
Using the above definitions, a vector space can be described as a commutative group combined with a field that satisfies the scaling properties , , , , , for , .
A central interest in data science is to seek simple description of complex objects. A typical situation is that many instances of some object of interest are initially given as an -tuple with large . Assuming that addition and scaling of such objects can cogently be defined, a vector space is obtained, say over the field of reals with an Euclidean distance, . Examples include for instance recordings of medical data (electroencephalograms, electrocardiograms), sound recordings, or images, for which can easily reach in to the millions. A natural question to ask is whether all the real numbers are actually needed to describe the observed objects, or perhaps there is some intrinsic description that requires a much smaller number of descriptive parameters, that still preserves the useful idea of linear combination. The mathematical transcription of this idea is a vector subspace.
The above states a vector subspace must be closed under linear combination, and have the same vector addition and scaling operations as the enclosing vector space. The simplest vector subspace of a vector space is the null subspace that only contains the null element, . In fact any subspace must contain the null element , or otherwise closure would not be verified for the particular linear combination . If , then is said to be a proper subspace of , denoted by .
Setting components equal to zero in the real space defines a proper subspace whose elements can be placed into a one-to-one correspondence with the vectors within . For example, setting component of equal to zero gives that while not a member of , is in a one-to-one relation with . Dropping the last component of , gives vector , but this is no longer a one-to-one correspondence since for some given , the last component could take any value.
Vector subspaces arise in decomposition of a vector space. The converse, composition of vector spaces is also defined in terms of linear combination. A vector can be obtained as the linear combination
but also as
for some arbitrary . In the first case, is obtained as a unique linear combination of a vector from the set with a vector from . In the second case, there is an infinity of linear combinations of a vector from with another from to the vector . This is captured by a pair of definitions to describe vector space composition.
Since the same scalar field, vector addition, and scaling is used , it is more convenient to refer to vector space sums simply by the sum of the vector sets , or , instead of specifying the full tuplet for each space. This shall be adopted henceforth to simplify the notation.
In the previous example, the essential difference between the two ways to express is that , but , and in general if the zero vector is the only common element of two vector spaces then the sum of the vector spaces becomes a direct sum.In practice, the most important procedure to construct direct sums or check when an intersection of two vector subspaces reduces to the zero vector is through an inner product.
The above concept of orthogonality can be extended to other vector subspaces, such as spaces of functions. It can also be extended to other choices of an inner product, in which case the term conjugate vector spaces is sometimes used.
The concepts of sum and direct sum of vector spaces used linear combinations of the form . This notion can be extended to arbitrary linear combinations.
Note that for real vector spaces a member of the span of the vectors is the vector obtained from the matrix vector multiplication
From the above, the span is a subset of the co-domain of the linear mapping .
The wide-ranging utility of linear algebra essentially results a complete characterization of the behavior of a linear mapping between vector spaces , . For some given linear mapping the questions that arise are:
Can any vector within be obtained by evaluation of ?
Is there a single way that a vector within can be obtained by evaluation of ?
Linear mappings between real vector spaces , have been seen to be completely specified by a matrix . It is common to frame the above questions about the behavior of the linear mapping through sets associated with the matrix . To frame an answer to the first question, a set of reachable vectors is first defined.
By definition, the column space is included in the co-domain of the function , , and is readily seen to be a vector subspace of . The question that arises is whether the column space is the entire co-domain that would signify that any vector can be reached by linear combination. If this is not the case then the column space would be a proper subset, , and the question is to determine what part of the co-domain cannot be reached by linear combination of columns of . Consider the orthogonal complement of defined as the set vectors orthogonal to all of the column vectors of , expressed through inner products as
This can be expressed more concisely through the transpose operation
and leads to the definition of a set of vectors for which
Note that the left null space is also a vector subspace of the co-domain of , . The above definitions suggest that both the matrix and its transpose play a role in characterizing the behavior of the linear mapping , so analagous sets are define for the transpose .
The above low dimensional examples are useful to gain initial insight into the significance of the spaces . Further appreciation can be gained by applying the same concepts to processing of images. A gray-scale image of size by pixels can be represented as a vector with components, . Even for a small image with pixels along each direction, the vector would have components. An image can be specified as a linear combination of the columns of the identity matrix
with the gray-level intensity in pixel . Similar to the inclined plane example from §1, an alternative description as a linear combination of another set of vectors might be more relevant. One choice of greater utility for image processing mimics the behavior of the set that extends the second example in §1, would be for
For the simple scalar mapping , , the condition implies either that or . Note that can be understood as defining a zero mapping . Linear mappings between vector spaces, , can exhibit different behavior, and the condtion , might be satisfied for both , and . Analogous to the scalar case, can be understood as defining a zero mapping, .
In vector space , vectors related by a scaling operation, , , are said to be colinear, and are considered to contain redundant data. This can be restated as , from which it results that . Colinearity can be expressed only in terms of vector scaling, but other types of redundancy arise when also considering vector addition as expressed by the span of a vector set. Assuming that , then the strict inclusion relation holds. This strict inclusion expressed in terms of set concepts can be transcribed into an algebraic condition.
Introducing a matrix representation of the vectors
allows restating linear dependence as the existence of a non-zero vector, , such that . Linear dependence can also be written as , or that one cannot deduce from the fact that the linear mapping attains a zero value that the argument itself is zero. The converse of this statement would be that the only way to ensure is for , or , leading to the concept of linear independence.
Vector spaces are closed under linear combination, and the span of a vector set defines a vector subspace. If the entire set of vectors can be obtained by a spanning set, , extending by an additional element would be redundant since . This is recognized by the concept of a basis, and also allows leads to a characterization of the size of a vector space by the cardinality of a basis set.
The domain and co-domain of the linear mapping , , are decomposed by the spaces associated with the matrix . When , , the following vector subspaces associated with the matrix have been defined:
the column space of
the row space of
the null space of
the left null space of , or null space of
A partition of a set has been introduced as a collection of subsets such that any given element belongs to only one set in the partition. This is modified when applied to subspaces of a vector space, and a partition of a set of vectors is understood as a collection of subsets such that any vector except belongs to only one member of the partition.
Linear mappings between vector spaces can be represented by matrices with columns that are images of the columns of a basis of
Consider the case of real finite-dimensional domain and co-domain, , in which case ,
The column space of is a vector subspace of the codomain, , but according to the definition of dimension if there remain non-zero vectors within the codomain that are outside the range of ,
All of the non-zero vectors in , namely the set of vectors orthogonal to all columns in fall into this category. The above considerations can be stated as
The question that arises is whether there remain any non-zero vectors in the codomain that are not part of or . The fundamental theorem of linear algebra states that there no such vectors, that is the orthogonal complement of , and their direct sum covers the entire codomain .
In the vector space the subspaces are said to be orthogonal complements is , and . When , the orthogonal complement of is denoted as , .
Consideration of equality between sets arises in proving the above theorem. A standard technique to show set equality , is by double inclusion, . This is shown for the statements giving the decomposition of the codomain . A similar approach can be used to decomposition of .
(column space is orthogonal to left null space).
( is the only vector both in and ).
The remainder of the FTLA is established by considering , e.g., since it has been established in (v) that , replacing yields , etc.
A vector space can be formed from all linear mappings from the vector space to another vector space
with addition and scaling of linear mappings defined by and . Let denote a basis for the domain of linear mappings within , such that the linear mapping is represented by the matrix
When the domain and codomain are the real vector spaces , , the above is a standard matrix of real numbers, . For linear mappings between infinite dimensional vector spaces the matrix is understood in a generalized sense to contain an infinite number of columns that are elements of the codomain . For example, the indefinite integral is a linear mapping between the vector space of functions that allow differentiation to any order,
and for the monomial basis , is represented by the generalized matrix
Truncation of the basis expansion where to terms, and sampling of at points , forms a standard matrix of real numbers
As to be expected, matrices can also be organized as vector space , which is essentially the representation of the associated vector space of linear mappings,
The addition and scaling of matrices is given in terms of the matrix components by
From the above it is apparent that linear mappings and matrices can also be considered as data, and a first step in analysis of such data is definition of functionals that would attach a single scalar label to each linear mapping of matrix. Of particular interest is the definition of a norm functional that characterizes in an appropriate sense the size of a linear mapping.
Consider first the case of finite matrices with real components that represent linear mappings between real vector spaces . The columns of could be placed into a single column vector with components
Subsequently the norm of the matrix could be defined as the norm of the vector . An example of this approach is the Frobenius norm
A drawback of the above approach is that the structure of the matrix and its close relationship to a linear mapping is lost. A more useful characterization of the size of a mapping is to consider the amplification behavior of linear mapping. The motivation is readily understood starting from linear mappings between the reals , that are of the form . When given an argument of unit magnitude , the mapping returns a real number with magnitude . For mappings within the plane, arguments that satisfy are on the unit circle with components have images through given analytically by
and correspond to ellipses.
From the above the mapping associated amplifies some directions more than others. This suggests a definition of the size of a matrix or a mapping by the maximal amplification unit norm vectors within the domain.
In the above, any vector norm can be used within the domain and codomain.
The fundamental theorem of linear algebra partitions the domain and codomain of a linear mapping . For real vectors spaces , the partition properties are stated in terms of spaces of the associated matrix as
The dimension of the column and row spaces is the rank of the matrix, is the nullity of , and is the nullity of . A infinite number of bases could be defined for the domain and codomain. It is of great theoretical and practical interest bases with properties that faciliatate insight or computation.
The above partitions of the domain and codomain are orthogonal, and suggest searching for orthogonal bases within these subspaces. Introduce a matrix representation for the bases
with and . Orthogonality between columns , for is expressed as . For , the inner product is positive , and since scaling of the columns of preserves the spanning property , it is convenient to impose . Such behavior is concisely expressed as a matrix product
with the identity matrix in . Expanded in terms of the column vectors of the first equality is
It is useful to determine if a matrix exists such that , or
The columns of are the coordinates of the column vectors of in the basis , and can readily be determined
where is the column of , hence , leading to
Note that the second equality
acts as normalization condition on the matrices .
Given a linear mapping , expressed as , the simplest description of the action of would be a simple scaling, as exemplified by that has as its associated matrix . Recall that specification of a vector is typically done in terms of the identity matrix , but may be more insightfully given in some other basis . This suggests that especially useful bases for the domain and codomain would reduce the action of a linear mapping to scaling along orthogonal directions, and evaluate by first re-expressing in another basis , and re-expressing in another basis , . The condition that the linear operator reduces to simple scaling in these new bases is expressed as for , with the scaling coefficients along each direction which can be expressed as a matrix vector product , where is of the same dimensions as and given by
Imposing the condition that are orthogonal leads to
which can be replaced into to obtain
From the above the orthogonal bases and scaling coefficients that are sought must satisfy .
The scaling coefficients are called the singular values of . The columns of are called the left singular vectors, and those of are called the right singular vectors.
The fact that the scaling coefficients are norms of and submatrices of , , is crucial importance in applications. Carrying out computation of the matrix products
leads to a representation of as a sum
Each product is a matrix of rank one, and is called a rank-one update. Truncation of the above sum to terms leads to an approximation of
In very many cases the singular values exhibit rapid, exponential decay, , such that the approximation above is an accurate representation of the matrix .
The SVD can be used to solve common problems within linear algebra.
To change from vector coordinates in the canonical basis to coordinates in some other basis , a solution to the equation can be found by the following steps.
Compute the SVD, ;
Find the coordinates of in the orthogonal basis , ;
Scale the coordinates of by the inverse of the singular values , , such that is satisfied;
Find the coordinates of in basis , .
In the above was assumed to be a basis, hence . If columns of do not form a basis, , then might not be reachable by linear combinations within . The closest vector to in the norm is however found by the same steps, with the simple modification that in Step 3, the scaling is carried out only for non-zero singular values, , .
From the above, finding either the solution of or the best approximation possible if is not of full rank, can be written as a sequence of matrix multiplications using the SVD
where the matrix (notice the inversion of dimensions) is defined as a matrix with elements on the diagonal, and is called the pseudo-inverse of . Similarly the matrix
that allows stating the solution of simply as is called the pseudo-inverse of . Note that in practice is not explicitly formed. Rather the notation is simply a concise reference to carrying out steps 1-4 above.
A typical scenario in many sciences is acquisition of numbers to describe some object that is understood to actually require only parameters. For example, voltage measurements of an alternating current could readily be reduced to three parameters, the amplitude, phase and frequency . Very often a simple first-degree polynomial approximation is sought for a large data set . All of these are instances of data compression, a problem that can be solved in a linear algebra framework.
Consider a partition of a vector space into orthogonal subspaces , , . Within the typical scenario described above , , , , . If is a basis for and is a basis for W, then is a basis for . Even though the matrices are not necessarily square, they are said to be orthogonal, in the sense that all columns are of unit norm and orthogonal to one another. Computation of the matrix product leads to the formation of the identity matrix within
Similarly, . Whereas for the square orthogonal matrix multiplication both on the left and the right by its transpose leads to the formation of the identity matrix
the same operations applied to rectangular orthogonal matrices lead to different results
A simple example is provided by taking , the first columns of the identity matrix in which case
Applying to some vector leads to a vector whose first components are those of , and the remaining are zero. The subtraction leads to a new vector that has the first components equal to zero, and the remaining the same as those of . Such operations are referred to as projections, and for correspond to projection onto the span.
Returning to the general case, the orthogonal matrices , , are associated with linear mappings , , . The mapping gives the components in the basis of a vector whose components in the basis are . The mappings project a vector onto span, span, respectively. When are orthogonal matrices the projections are also orthogonal . Projection can also be carried out onto nonorthogonal spanning sets, but the process is fraught with possible error, especially when the angle between basis vectors is small, and will be avoided henceforth.
Notice that projection of a vector already in the spanning set simply returns the same vector, which leads to a general definition.
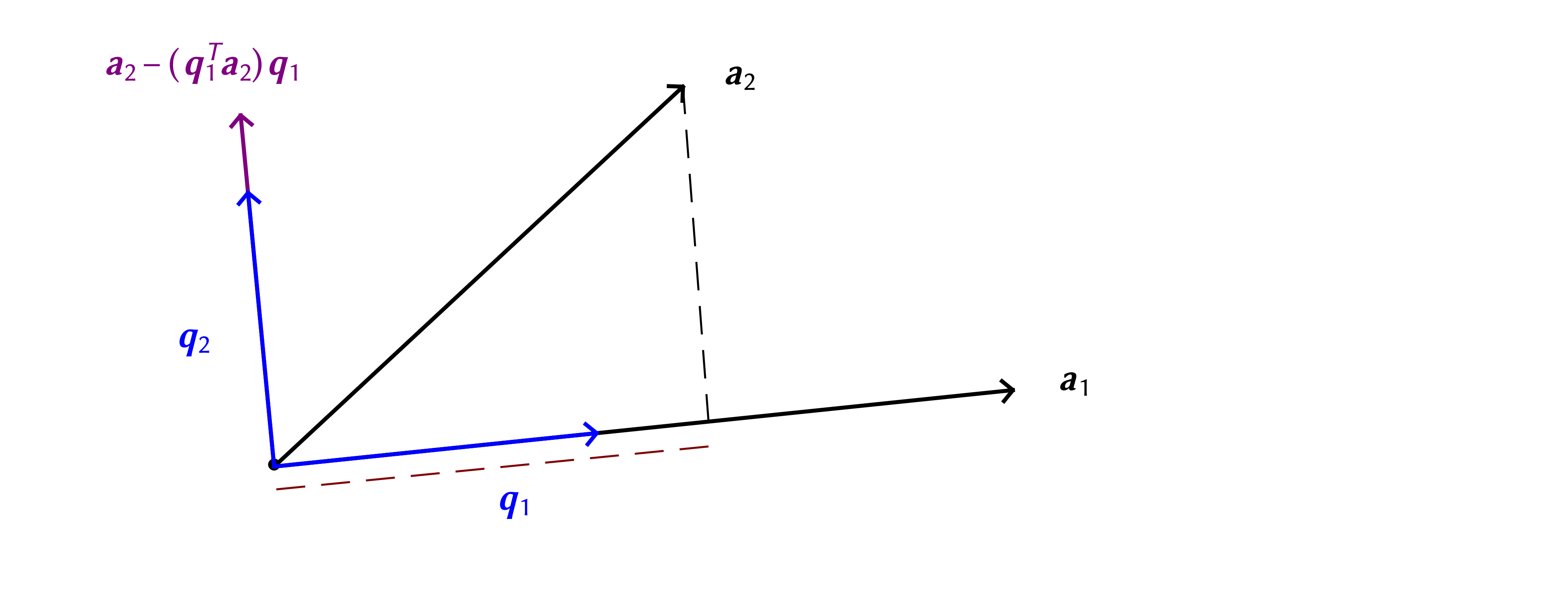
Orthonormal vector sets are of the greatest practical utility, leading to the question of whether some such a set can be obtained from an arbitrary set of vectors . This is possible for independent vectors, through what is known as the Gram-Schmidt algorithm
Start with an arbitrary direction
Divide by its norm to obtain a unit-norm vector
Choose another direction
Subtract off its component along previous direction(s)
Divide by norm
Repeat the above

The above geometrical description can be expressed in terms of matrix operations as
equivalent to the system
The system is easily solved by forward substitution resulting in what is known as the (modified) Gram-Schmidt algorithm, transcribed below both in pseudo-code and in Octave.
Note that the normalization condition is satisifed by two values , so results from the above implementation might give orthogonal vectors of different orientations than those returned by the Octave qr function. The implementation provided by computational packages such as Octave contain many refinements of the basic algorithm and it's usually preferable to use these in applications.
By analogy to arithmetic and polynomial algebra, the Gram-Schmidt algorithm furnishes a factorization
with with orthonormal columns and an upper triangular matrix, known as the -factorization. Since the column vectors within were obtained through linear combinations of the column vectors of we have
The -factorization can be used to solve basic problems within linear algebra.
Recall that when given a vector , an implicit basis is assumed, the canonical basis given by the column vectors of the identity matrix . The coordinates in another basis can be found by solving the equation
by an intermediate change of coordinates to the orthogonal basis . Since the basis is orthogonal the relation holds, and changes of coordinates from to , are easily computed . Since matrix multiplication is associative
the relations are obtained, stating that also contains the coordinates of in the basis . The three steps are:
Compute the -factorization, ;
Find the coordinates of in the orthogonal basis , ;
Find the coordinates of in basis , .
Since is upper-triangular,
the coordinates of in the basis are easily found by back substitution.
The above operations are carried out in the background by the Octave backslash operation A\b to solve A*x=b, inspired by the scalar mnemonic . Again, many additional refinements of the basic algorithm argue for using the built-in Octave functions, even though the above implementations can be verified as correct.
The above approch for the real vector space can be used to determine orthogonal bases for any other vector space by appropriate modification of the scalar product. For example, within the space of smooth functions that can differentiated an arbitrary number of times, the Taylor series
is seen to be a linear combination of the monomial basis with scaling coefficients . The scalar product
can be seen as the extension to the continuum of a the vector dot product. Orthogonalization of the monomial basis with the above scalar product leads to the definition of another family of polynomials, known as the Legendre polynomials
The Legendre polynomials are usually given with a different scaling such that , rather than the unit norm condition . The above results can be recovered by sampling of the interval at points , , , by approximation of the integral by a Riemann sum
The approach to compressing data suggested by calculus concepts is to form the sum of squared differences between and , for example for when carrying out linear regression,
and seek that minimize . The function can be thought of as the height of a surface above the plane, and the gradient is defined as a vector in the direction of steepest slope. When at some point on the surface if the gradient is different from the zero vector , travel in the direction of the gradient would increase the height, and travel in the opposite direction would decrease the height. The minimal value of would be attained when no local travel could decrease the function value, which is known as stationarity condition, stated as . Applying this to determining the coefficients of a linear regression leads to the equations
The above calculations can become tedious, and do not illuminate the geometrical essence of the calculation, which can be brought out by reformulation in terms of a matrix-vector product that highlights the particular linear combination that is sought in a liner regression. Form a vector of errors with components , which for linear regression is . Recognize that is a linear combination of and with coefficients , or in vector form
The norm of the error vector is smallest when is as close as possible to . Since is within the column space of , , the required condition is for to be orthogonal to the column space
The above is known as the normal system, with is the normal matrix. The system can be interpreted as seeking the coordinates in the basis of the vector . An example can be constructed by randomly perturbing a known function to simulate measurement noise and compare to the approximate obtained by solving the normal system.
Generate some data on a line and perturb it by some random quantities
Form the matrices , , vector
Solve the system , and form the linear combination closest to
The normal matrix basis can however be an ill-advised choice. Consider given by
where the first column vector is taken from the identity matrix , and second is the one obtained by rotating it with angle . If , the normal matrix is orthogonal, , but for small , and are approximated as
When is small are almost colinear, and even more so. This can lead to amplification of small errors, but can be avoided by recognizing that the best approximation in the 2-norm is identical to the Euclidean concept of orthogonal projection. The orthogonal projector onto is readily found by -factorization, and the steps to solve least squares become
Compute
The projection of onto the column space of is , and has coordinates in the orthogonal basis .
The same can also obtained by linear combination of the columns of , , and replacing with its -factorization gives , that leads to the system , solved by back-substitution.
The above procedure carried over to approximation by higher degree polynomials.

The least-squares problem
focuses on a simpler representation of a data vector as a linear combination of column vectors of . Consider some phenomenon modeled as a function between vector spaces , such that for input parameters , the state of the system is . For most models is differentiable, a transcription of the condition that the system should not exhibit jumps in behavior when changing the input parameters. Then by appropriate choice of units and origin, a linearized model
is obtained if , expressed as (1) if .
A simpler description is often sought, typically based on recognition that the inputs and outputs of the model can themselves be obtained as linear combinations , , involving a smaller set of parameters , , , . The column spaces of the matrices , are vector subspaces of the original set of inputs and outputs, , . The sets of column vectors of each form a reduced basis for the system inputs and outputs if they are chosed to be of full rank. The reduced bases are assumed to have been orthonormalized through the Gram-Schmidt procedure such that , and . Expressing the model inputs and outputs in terms of the reduced basis leads to
The matrix is called the reduced system matrix and is associated with a mapping , that is a restriction to the vector subspaces of the mapping . When is an endomorphism, , , the same reduced basis is used for both inputs and outputs, , , and the reduced system is
Since is assumed to be orthogonal, the projector onto is . Applying the projector on the inital model
leads to , and since the relation is obtained, and conveniently grouped as
again leading to the reduced model . The above calculation highlights that the reduced model is a projection of the full model on .
Consider two functions , that represent data streams in time of inputs and outputs of some system. A basic question arising in modeling and data science is whether the inputs and outputs are themselves in a functional relationship. This usually is a consequence of incomplete knowledge of the system, such that while might be assumed to be the most relevant input, output quantities, this is not yet fully established. A typical approach is to then carry out repeated measurements leading to a data set , thus defining a relation. Let denote vectors containing the input and output values. The mean values of the input and output are estimated by the statistics
where is the expectation seen to be a linear mapping, whose associated matrix is
and the means are also obtained by matrix vector multiplication (linear combination),
Deviation from the mean is measured by the standard deviation defined for by
Note that the standard deviations are no longer linear mappings of the data.
Assume that the origin is chosen such that . One tool to estalish whether the relation is also a function is to compute the correlation coefficient
that can be expressed in terms of a scalar product and 2-norm as
Squaring each side of the norm property , leads to
known as the Cauchy-Schwarz inequality, which implies . Depending on the value of , the variables are said to be:
uncorrelated, if ;
correlated, if ;
anti-correlated, if .
The numerator of the correlation coefficient is known as the covariance of
The correlation coefficient can be interpreted as a normalization of the covariance, and the relation
is the two-variable version of a more general relationship encountered when the system inputs and outputs become vectors.
Consider now a related problem, whether the input and output parameters , thought to characterize a system are actually well chosen, or whether they are redundant in the sense that a more insightful description is furnished by with fewer components . Applying the same ideas as in the correlation coefficient, a sequence of measurements is made leading to data sets
Again, by appropriate choice of the origin the means of the above measurements is assumed to be zero
Covariance matrices can be constructed by
Consider now the SVDs of , , and from
identify , and .
Recall that the SVD returns an order set of singular values , and associated singular vectors. In many applications the singular values decrease quickly, often exponentially fast. Taking the first singular modes then gives a basis set suitable for mode reduction
Suppose now that admits a unique solution. How to find it? We are especially interested in constructing a general procedure, that will work no matter what the size of might be. This means we seek an algorithm that precisely specifies the steps that lead to the solution, and that we can program a computing device to carry out automatically. One such algorithm is Gaussian elimination.
Consider the system
The idea is to combine equations such that we have one fewer unknown in each equation. Ask: with what number should the first equation be multiplied in order to eliminate from sum of equation 1 and equation 2? This number is called a Gaussian multiplier, and is in this case . Repeat the question for eliminating from third equation, with multiplier .
Now, ask: with what number should the second equation be multiplied to eliminate from sum of second and third equations. The multiplier is in this case .
Starting from the last equation we can now find , replace in the second to obtain , hence , and finally replace in the first equation to obtain .
The above operations only involve coefficients. A more compact notation is therefore to work with what is known as the "bordered matrix"
Once the above triangular form has been obtain, the solution is found by back substitution, in which we seek to form the identity matrix in the first 3 columns, and the solution is obtained in the last column.
We have introduced Gaussian elimination as a procedure to solve the linear system ("find coordinates of vector in terms of column vectors of matrix "),
We now reinterpret Gaussian elimination as a sequence of matrix multiplications applied to to obtain a simpler, upper triangular form.
Consider the system
with
We ask if there is a matrix that could be multiplied with to produce a result with zeros under the main diagonal in the first column. First, gain insight by considering multiplication by the identity matrix, which leaves unchanged
In the first stage of Gaussian multiplication, the first line remains unchanged, so we deduce that should have the same first line as the identity matrix
Next, recall the way Gaussian multipliers were determined: find number to multiply first line so that added to second, third lines a zero is obtained. This leads to the form
Finally, identify the missing entries with the Gaussian multipliers to determine
Verify by carrying out the matrix multiplication
Repeat the above reasoning to come up with a second matrix that forms a zero under the main diagonal in the second column
We have obtained a matrix with zero entries under the main diagonal (an upper triangular matrix) by a sequence of matrix multiplications.
From the above, we assume that we can form a sequence of multiplier matrices such that the result is an upper triangular matrix
Recall the basic operation in row echelon reduction: constructing a linear combination of rows to form zeros beneath the main diagonal, e.g.
This can be stated as a matrix multiplication operation, with
For nonsingular, the successive steps in row echelon reduction (or Gaussian elimination) correspond to successive multiplications on the left by Gaussian multiplier matrices
The inverse of a Gaussian multiplier is
From obtain
Due to the simple form of the matrix is easily obtained as
We will show that this indeed possible if admits a unique solution. Furthermore, the product of lower triangular matrices is lower triangular, and the inverse of a lower triangular matrix is lower triangular (same applies for upper triangular matrices). Introduce the notation
and obtain
or
The above result permits a basic insight into Gaussian elimination: the procedure depends on "factoring" the matrix into two "simpler" matrices . The idea of representing a matrix as a product of simpler matrices is fundamental to linear algebra, and we will come across it repeatedly.
For now, the factorization allows us to devise the following general approach to solving
Find the factorization
Insert the factorization into to obtain , where the notation has been introduced. The system
is easy to solve by forward substitution to find for given
Finally find by backward substitution solution of
Given
By analogy to the simple scalar equation with solution when , we are interested in writing the solution to a linear system as for , . Recall that solving corresponds to expressing the vector as a linear combination of the columns of . This can only be done if the columns of form a basis for , in which case we say that is non-singular.
Computation of the inverse can be carried out by repeated use of Gauss elimination. Denote the inverse by for a moment and consider the inverse matrix property . Introducing the column notation for leads to
and identification of each column in the equality states
with the column unit vector with zero components everywhere except for a in row . To find the inverse we need to simultaneously solve the linear systems given above.
Gauss-Jordan algorithm example. Consider
To find the inverse we solve the systems . This can be done simultaneously by working with the matrix bordered by
Carry out now operations involving linear row combinations and permutations to bring the left side to
to obtain
a square matrix, is the oriented volume enclosed by the column vectors of (a parallelipiped)
Geometric interpretation of determinants
Determinant calculation rules
Algebraic definition of a determinant
Computation of a determinant with
Computation of a determinant with
Where do these determinant computation rules come from? Two viewpoints
Geometric viewpoint: determinants express parallelepiped volumes
Algebraic viewpoint: determinants are computed from all possible products that can be formed from choosing a factor from each row and each column
In two dimensions a “parallelepiped” becomes a parallelogram with area given as
Take as the base, with length . Vector is at angle to -axis, is at angle to -axis, and the angle between , is . The height has length
Use , , ,
The geometric interpretation of a determinant as an oriented volume is useful in establishing rules for calculation with determinants:
Determinant of matrix with repeated columns is zero (since two edges of the parallelepiped are identical). Example for
This is more easily seen using the column notation
Determinant of matrix with linearly dependent columns is zero (since one edge lies in the 'hyperplane' formed by all the others)
Separating sums in a column (similar for rows)
with
Scalar product in a column (similar for rows)
with
Linear combinations of columns (similar for rows)
with .
A determinant of size can be expressed as a sum of determinants of size by expansion along a row or column
The formal definition of a determinant
requires operations, a number that rapidly increases with
A more economical determinant is to use row and column combinations to create zeros and then reduce the size of the determinant, an algorithm reminiscent of Gauss elimination for systems
Example:
The first equality comes from linear combinations of rows, i.e. row 1 is added to row 2, and row 1 multiplied by 2 is added to row 3. These linear combinations maintain the value of the determinant. The second equality comes from expansion along the first column
Consider . We've introduced the idea of a scalar product
in which from two vectors one obtains a scalar
We've also introduced the idea of an exterior product
in which a matrix is obtained from two vectors
Another product of two vectors is also useful, the cross product, most conveniently expressed in determinant-like form
In reduction of the model
by restriction to a subspaces spanned by the orthogonal column vectors of , , , the reduced model
is obtained with , the reduced system matrix. The choice of the basis sets is not yet specified. One common choice is to use the singular value decomposition and choose the dominant singular vectors to span the subspaces,
This assumes that an SVD is available, and that ordering of vectors by the -norm is relevant to the problem. This is often the case in problems in which the matrix somewhow expresses the energy of a system. For example in deformation of a structure a relationship between forces and displacements is approximated linearly by , with the stiffness matrix expressing the potential energy stored in the deformation.
However in many cases, the model might not express an energy so the 2-norm is not an appropriate functional, or even if it is the size of the problem might render the computation of the singular value decomposition impractical. In such situations alternative procedures to construct reduced bases must be devised.
Consider that the only information available about the problem are the matrix and a vector . From these two a sequence of vectors can be gather into what is known as a Krylov matrix
The Krylov matrix is generally not orthogonal, but an orthogonal basis can readily be extracted through the factorization
The basis can then be adopted, both for the domain and the codomain
The Krylov procedure has the virtue of simplicity, but does not have the desirable property of the SVD of ordering of the singular vectors. Suppose that the system matrix is applied to vectors , leading to formation of the vector set . Denote by the first members of the set ordered in some arbitrary norm
where denotes the permutation that orders the vectors in accordance with the chosen norm. The above is called a greedy approximation, and furnishes an alternative to the SVD that exhibits an ordering property. As in the Krylov case, it is usually more efficient to use an orthogonal set obtained through factorization
Consider square matrix . The eigenvalue problem asks for vectors , , scalars such that
Eigenvectors are those special vectors whose direction is not modified by the matrix
Rewrite (1): , and deduce that must be singular in order to have non-trivial solutions
Consider the determinant
From determinant definition “sum of all products choosing an element from row/column”
is the characteristic polynomial associated with the matrix , and is of degree
has characteristic polynomial of degree , which has roots (Fundamental theorem of algebra)
Example
For , the eigenvalue problem 5 () can be written in matrix form as
If the column vectors of are linearly independent, then is invertible and can be reduced to diagonal form
Diagonal forms are useful in solving linear ODE systems
Also useful in repeatedly applying
When can a matrix be reduced to diagonal form? When eigenvectors are linearly independent such that the inverse of exists
Matrices with distinct eigenvalues are diagonalizable. Consider with eigenvalues for ,
Proof. By contradiction. Take any two eigenvalues and assume that would depend linearly on , for some . Then
and subtracting would give . Since is an eigenvector, hence we obtain a contradiction .
The characteristic polynomial might have repeated roots. Establishing diagonalizability in that case requires additional concepts
Example. has two single roots , and a repeated root . The eigenvalue has an algebraic multiplicity of 2
Finding eigenvalues as roots of the characteristic polynomial is suitable for small matrices .
analytical root-finding formulas are available only for
small errors in characteristic polynomial coefficients can lead to large errors in roots
Octave/Matlab procedures to find characteristic polynomial
poly(A) function returns the coefficients
roots(p) function computes roots of the polynomial
Find eigenvectors as non-trivial solutions of system
Note convenient choice of row operations to reduce amount of arithmetic, and use of knowledge that is singular to deduce that last row must be null
In traditional form the above row-echelon reduced system corresponds to
In Octave/Matlab the computations are carried out by the null function
The eigenvalues of are , but small errors in numerical computation can give roots of the characteristic polynomial with imaginary parts
In the following example notice that if we slightly perturb (by a quantity less than 0.0005=0.05%), the eigenvalues get perturb by a larger amount, e.g. 0.13%.
Extracting eigenvalues and eigenvectors is a commonly encountered operation, and specialized functions exist to carry this out, including the eig function
Recall definitions of eigenvalue algebraic and geometric multiplicities .
The SVD is determined by eigendecomposition of , and
, an eigendecomposition of . The columns of are eigenvectors of and called right singular vectors of
, an eigendecomposition of . The columns of are eigenvectors of and called left singular vectors of
The matrix has form
and are the singular values of .
The singular value decomposition (SVD) furnishes complete information about
(the number of non-zero singular values)
are orthogonal basis for the domain and codomain of
The trigonometric functions have been introduced as a particularly appropriate basis for periodic functions. The functions are also known as solution of the homogeneous differential equation
The diferential operator is a linear mapping
and hence has an associated linear mapping. An approximation of the second-order differentiation operation is given by the finite difference formulas
octave] |