MATH566 Lesson 9: Chebyshev grid interpolation - preliminaries

Overview

Motivation: minimize interpolation error

by choosing sample points $x_j$ to ensure $w\left(t\right)$ remains small when $t\ne x_j$. We first review the concept of orthonormal bases.

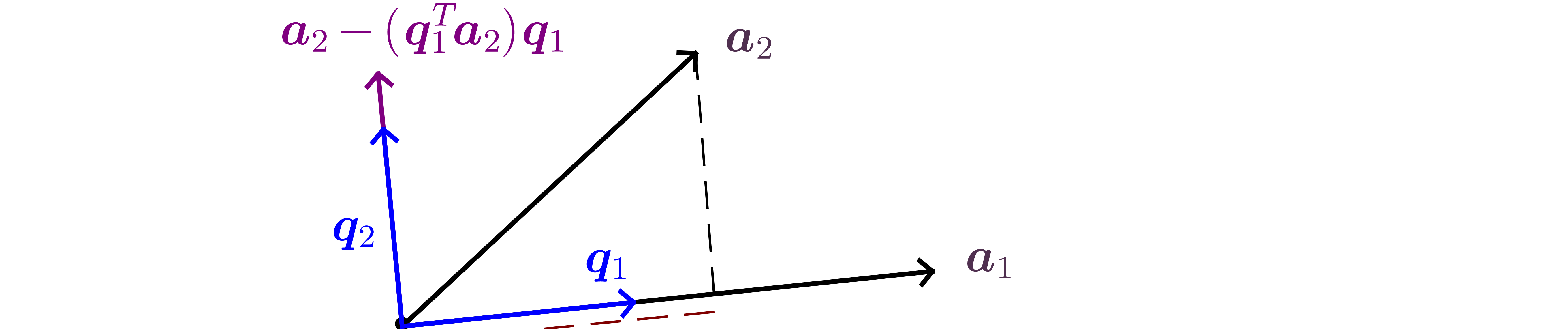
• Orthogonal matrices

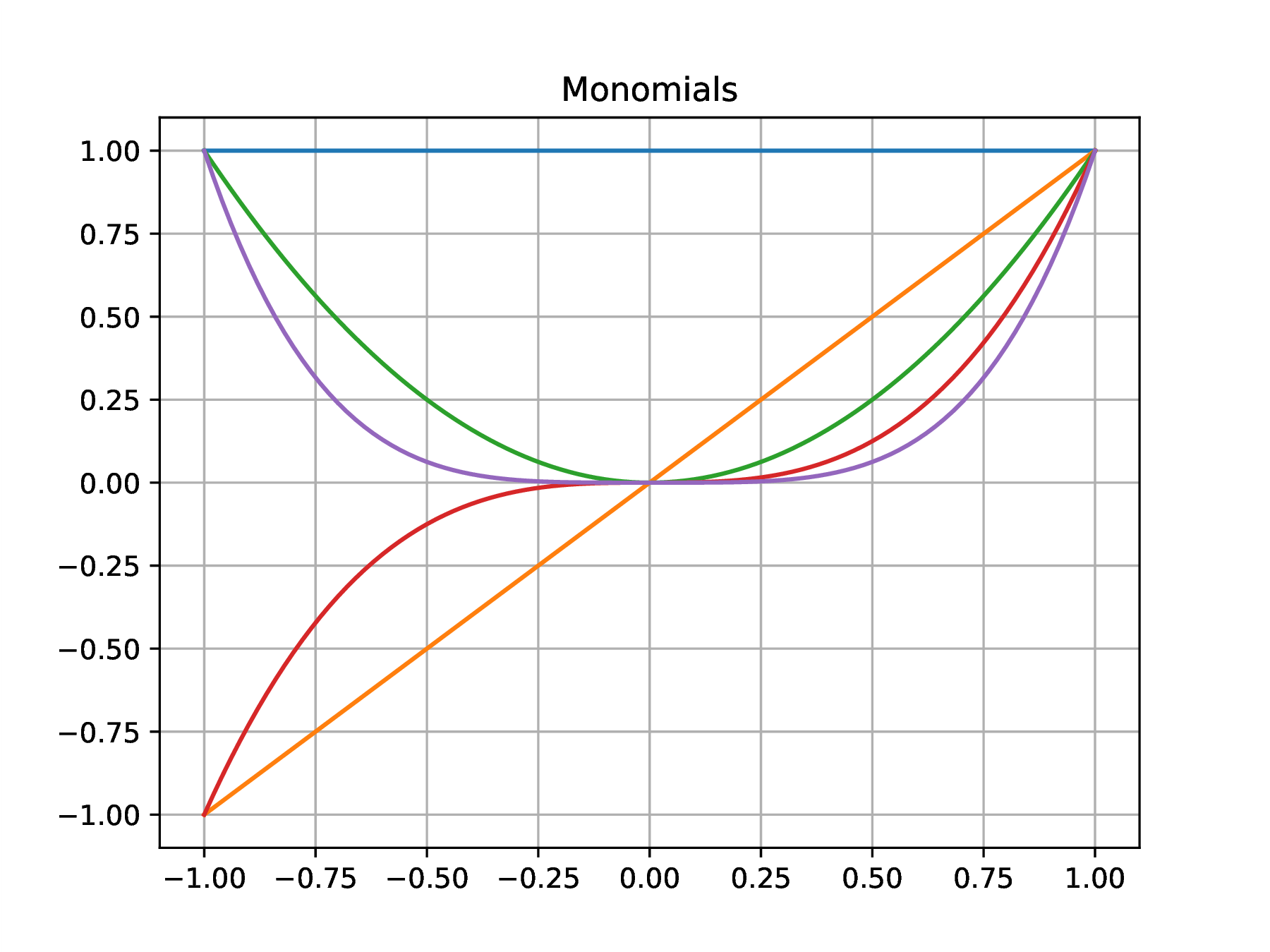
• Orthogonal polynomials

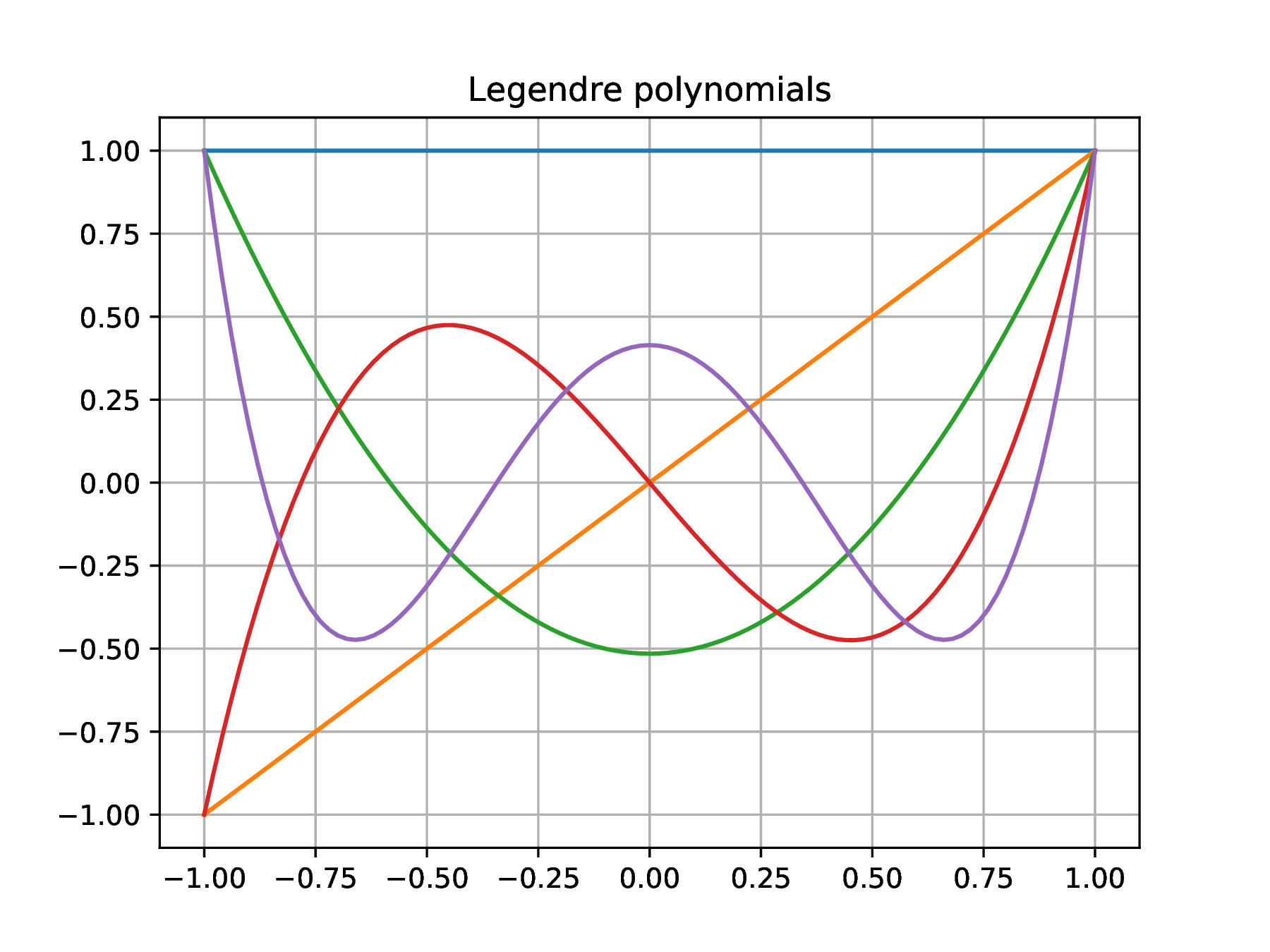
• Legendre polynomials

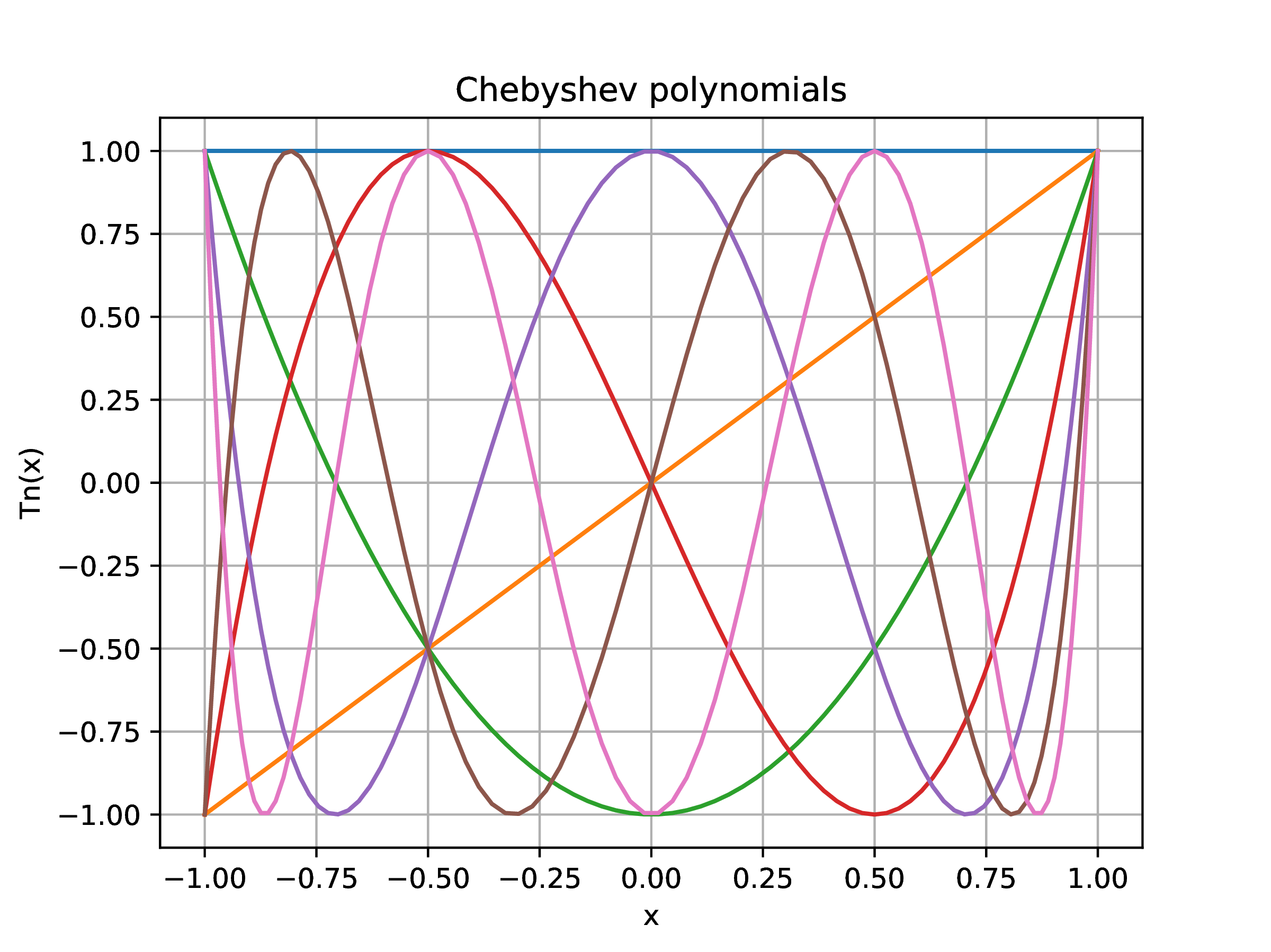
• Chebyshev polynomials

Orthogonal matrices

• Linear algebra: most effective bases in ${ℝ}^m$ are orthonormal, e.g. column vectors of the identity matrix

  ${\displaystyle 𝑰=\left[\begin{array}{llll}{𝒆}_1& {𝒆}_2& \dots & {𝒆}_m\end{array}\right]}$

• In general $𝑸=\left[\begin{array}{llll}{𝒒}_1& {𝒒}_2& \dots & {𝒒}_m\end{array}\right]\in {ℝ}^{m\times m}$ is an orthogonal matrix if the scalar product of two column vectors satisfies

  ${\displaystyle {𝒒}_i^T{𝒒}_j={\delta }_{ij},{𝑸}^T𝑸=\left[\begin{array}{l}{𝒒}_1^T\\ {𝒒}_2^T\\ ⋮\\ {𝒒}_m^T\end{array}\right]\left[\begin{array}{llll}{𝒒}_1& {𝒒}_2& \dots & {𝒒}_m\end{array}\right]=\left[\begin{array}{lll}{𝒒}_1^T{𝒒}_1& \dots & {𝒒}_1^T{𝒒}_m\\ ⋮& \ddots & ⋮\\ {𝒒}_m^T{𝒒}_1& \dots & {𝒒}_m^T{𝒒}_m\end{array}\right]=𝑰}$

• Recall: vectors are functions on the domain $\{1,2,\dots ,m\}$, e.g. $e_k\left(i\right)={\delta }_{ik}$

• The scalar product is expressed as

  ${\displaystyle {𝒒}_i^T{𝒒}_j={\delta }_{ij}=\sum _{l=1}^m{q}_i\left(l\right)q_j\left(l\right)}$

Orthogonalization: Gram-Schmidt process

• Assume $𝑨\in {ℝ}^{m\times m}$ is of full rank, i.e., has linearly independent columns

• Column vectors of $𝑨=\left[\begin{array}{lll}{𝒂}_1& \dots & {𝒂}_m\end{array}\right]$ may not be orthonormal, but an orthonormal basis can be obtained by the Gram-Schmidt process ($QR$ - factorization):

  1. Start with an arbitrary direction ${𝒂}_1$

  2. Divide by its norm to obtain a unit-norm vector ${𝒒}_1={𝒂}_1/||{𝒂}_1||$

  3. Choose another direction ${𝒂}_2$

  4. Subtract off its component along previous direction(s) ${𝒂}_2-\left({𝒒}_1^T{𝒂}_2\right){𝒒}_1$

  5. Divide by norm ${𝒒}_2=({𝒂}_2-\left({𝒒}_1^T{𝒂}_2\right){𝒒}_1)/||{𝒂}_2-\left({𝒒}_1^T{𝒂}_2\right){𝒒}_1||$

  6. Repeat the above

Orthogonal functions

• Extend scalar product ${𝒒}_i^T{𝒒}_j={\delta }_{ij}={\sum }_{l=1}^m{q}_i\left(l\right)q_j\left(l\right)$ to $f,g:[a,b]\to ℝ$

  ${\displaystyle (f,g)=\underset{a}{\overset{b}{\int }}\omega \left(t\right)f\left(t\right)g\left(t\right)dt}$

• The above is a (real-valued) a function inner product if:

  1. $(f,g)=(g,f)$

  2. $(af+bg,h)=a(f,h)+b(g,h)$

  3. $(f,f)>0$ and $(f,f)=0\Rightarrow f=0$

• Gram-Schmidt process can be applied to sets of functions $\{f_1,\dots ,f_m\}$ to obtain an orthonormal set $\{g_1,\dots ,g_m\}$ with respect to a specific inner product using norm $||f||={(f,f)}^{1/2}$

  1. $g_1=f_1/||f_1||$

  2. $h=f_2-(f_2,g_1)g_1$

  3. $g_2=h/||h||$

  4. $h=f_3-(f_3,g_1)g_1-(f_3,g_2)g_2$

  5. $g_3=h/||h||$, and continue

Legendre polynomials

• Orthogonal polynomials play an important role in numerical methods, they furnish a more effective basis than the monomial basis $\{1,t,t^2,\dots \}$ used in the Taylor series

• For scalar product with weight $\omega \left(t\right)=1$

  ${\displaystyle (f,g)=\underset{-1}{\overset{1}{\int }}f\left(t\right)g\left(t\right)dt}$

  applying the Gram-Schmidt process leads to the Legendre polynomials

Chebyshev polynomials

• Gram-Schmidt process applied to $\{1,t,t^2,\dots \}$ with scalar product

  ${\displaystyle (f,g)=\underset{-1}{\overset{1}{\int }}\frac{f\left(t\right)g\left(t\right)}{\sqrt{1-t^2}}dt}$

  leads to the Chebyshev polynomials, $T_n\left(t\right)$, $\omega \left(t\right)={(1-t^2)}^{-1/2}$

Figure 2. Chebyshev polynomials. Easily distinguishable. with values in $[-1,1]$, and roots clustered toward the interval endpoints