MATH566 Lesson 13: Root-finding

Overview

Motivation: A first application of function approximation is to devise procedures to find the roots or zeros of a real function of single variavle $f:[a,b]\to ℝ$. The procedures devised for scalar functions can be subsequently extended to multivariate and vector-valued functions

• Calculus of real functions of one variable

• The root-finding process

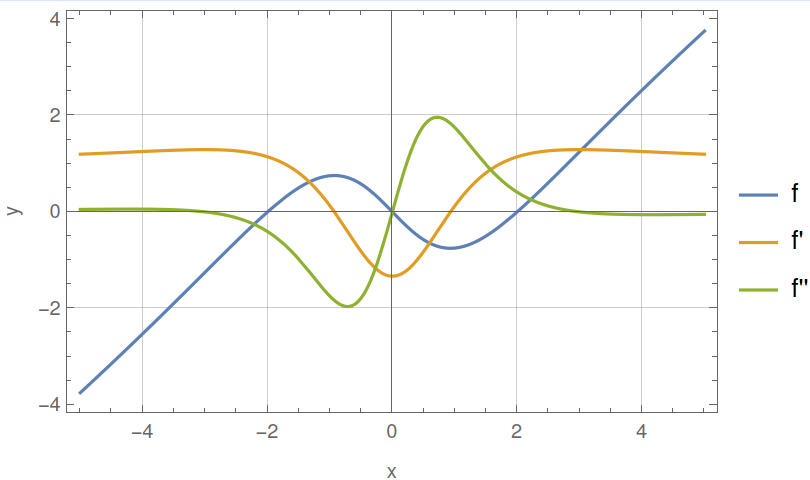
  • Root locations: qualitative plots

  • Interval reduction: bisection

Calculus of functions of one variable: Review

• Calculus is the study of continuous change, based upon the fundamental concepts of:

  Real numbers $ℝ$

  Functions $f:D\to C$

  Function limits ${lim}_{x\to c}f\left(x\right)$

• Real numbers measure continuous quantities and are graphically represented by the real axis

  

• $f$ associates input $x$ from $D$ (domain) to a single output $y$ from $C$ (codomain)

  $y=f\left(x\right)$ states that $y$ is the single output of the function $f$ for given input $x$

  $f$ is one-to-one if output $y$ is produced by a single input $x$, in which case $x=f^{-1}\left(y\right)$, $f^{-1}:C\to D$ is the inverse function of $f$.

• The limit ${lim}_{x\to c}f\left(x\right)$ describes the function $f$ at an infinity of points near to $c$.

  Formal definition: For any $\epsilon >0$ there exists a $\delta \left(\epsilon \right)$ such that from $|x-c|<\delta \left(\epsilon \right)$ it follows that $|f\left(x\right)-L|<\epsilon$.

Root-finding process

• Problem: $f:ℝ\to ℝ$, find $𝒵=\{z_k:f\left(z_k\right)=0,k\in 𝒦\}$ the null set of $f$

• Assume $𝒦\subset \mathbb{N}$, $\left|𝒦\right|=m>0$, $𝒵=\{z_k:f\left(z_k\right)=0,k=1,2,\dots ,m\}$

• Root-finding phases:

  • Root localization. Find intervals $[a_k,b_k]$, $a_k⩽z_k⩽b_k$, $z_j\notin [a_k,b_k]$ for $j\ne k$

    ${\displaystyle f\left(a_k\right)f\left(b_k\right)⩽0}$

  • Interval reduction (optional). Find sequence of smaller intervals containing a root: $[a_k^{\left(n\right)},b_k^{\left(n\right)}]\subset [a_k^{(n-1)},b_k^{(n-1)}]\subset \dots [a_k^{\left(1\right)},b_k^{\left(1\right)}]\subset [a_k^{\left(0\right)},b_k^{\left(0\right)}]=[a_k,b_k]$

  • Root refinement. Find approximation $z_k^{\left(n\right)}$ of $z_k$ to within:

    • maximum residual $\delta$, $\left|f\left(z_k^{\left(n\right)}\right)\right|⩽\delta$

    • maximum error $e$, $|z_k^{\left(n\right)}-z_k|⩽e$ replaced usually by $|z_k^{(n+1)}-z_k^{\left(n\right)}|⩽e$

    • maximum relative error $\epsilon$

      ${\displaystyle \frac{|z_k^{\left(n\right)}-z_k|}{\left|z_k\right|}⩽\epsilon ,\mathrm{replaced}\mathrm{by}\frac{|z_k^{(n+1)}-z_k^{\left(n\right)}|}{\left|z_k^{(n+1)}\right|}⩽\epsilon }$

Root-finding mathematical problem

• How hard is the root-finding problem?

• Define root-finding mathematical problem, mapping $F:X\to Y$

  • Input set $X=\{f:ℝ\to ℝ\}$, the set of functions whose zero sets are sought

  • Output set $Y=𝒵=\{z_k:f\left(z_k\right)=0,k=1,2,\dots ,m\}$, the zero sets

• Note: the mathematical root-finding problem $F$ is different from $f\in X$

• Example:

  • Find $z$ solution of $f\left(x\right)=ax+b=0$ for given $a,b\in ℝ$, $a\ne 0$.

    ${\displaystyle X=ℝ\backslash \left\{0\right\}\times ℝ,Y=ℝ,z_1=F(a,b)=-b/a.}$

    $F$ is differentiable and has condition number

    ${\displaystyle \kappa =||𝑱||,𝑱=\left[\begin{array}{ll}\frac{\partial F}{\partial a}& \frac{\partial F}{\partial b}\end{array}\right]=\left[\begin{array}{ll}-\frac{b}{a^2}& -\frac{1}{a}\end{array}\right]}$

    Intuitively, for $a\cong ϵ$, the root finding problem is hard, $\kappa \gg 1$.

• In general $\kappa =||\delta F/\delta f||$ Gateaux derivative w.r.t. to function $f$.

Interval reduction: bisection

• Idea:

  • Start from $[a,b]$ with $f\left(a\right)f\left(b\right)⩽0$

  • Obtain smaller interval by computing $f\left(c\right)$, $c=(a+b)/2=a+(b-a)/2$

    • If $f\left(a\right)f\left(c\right)<0$ then redefine $b=c$

    • If $f\left(c\right)f\left(b\right)<0$ then redefine $a=c$

• Obtain a sequence of intervals $[a_n,b_n]$ of decreasing length containing the root

  • $h_0=(b-a)$

  • $h_n=h_0/2^n=b_n-a_n$

  • $z\in [a_n,b_n]$

• At iteration $n$, $z_n\cong c_n$

  ${\displaystyle |z_n-z|⩽h_0/2^{n+1}}$

  Linear order of convergence

  ${\displaystyle \frac{|z_{n+1}-z|}{|z_n-z|}\cong \frac{1}{2}<1.}$

Bisection algorithm

• Computational complexity: one function evaluation ($f\left(c\right)$) per iteration

∴ 

function bisect(f,a,b,ε)
  if (a>b) a,b=b,a end
  fa=f(a); fb=f(b)
  δ=b-a; c=(a+b)/2
  while ((δ>ε) && (fa*fb<=0))
    δ=δ/2; c=a+δ; fc=f(c)
    if (fa*fc<=0)
      b,fb=c,fc
    else
      a,fa=c,fc
    end
  end
  return c
end;

∴ 

f(x)=x^2-2; a=1; b=2; ε=0.01;

∴ 

[bisect(f,a,b,ε) sqrt(2.0)]

∴