MATH566 Lesson 15: Nonlinear systems

Overview

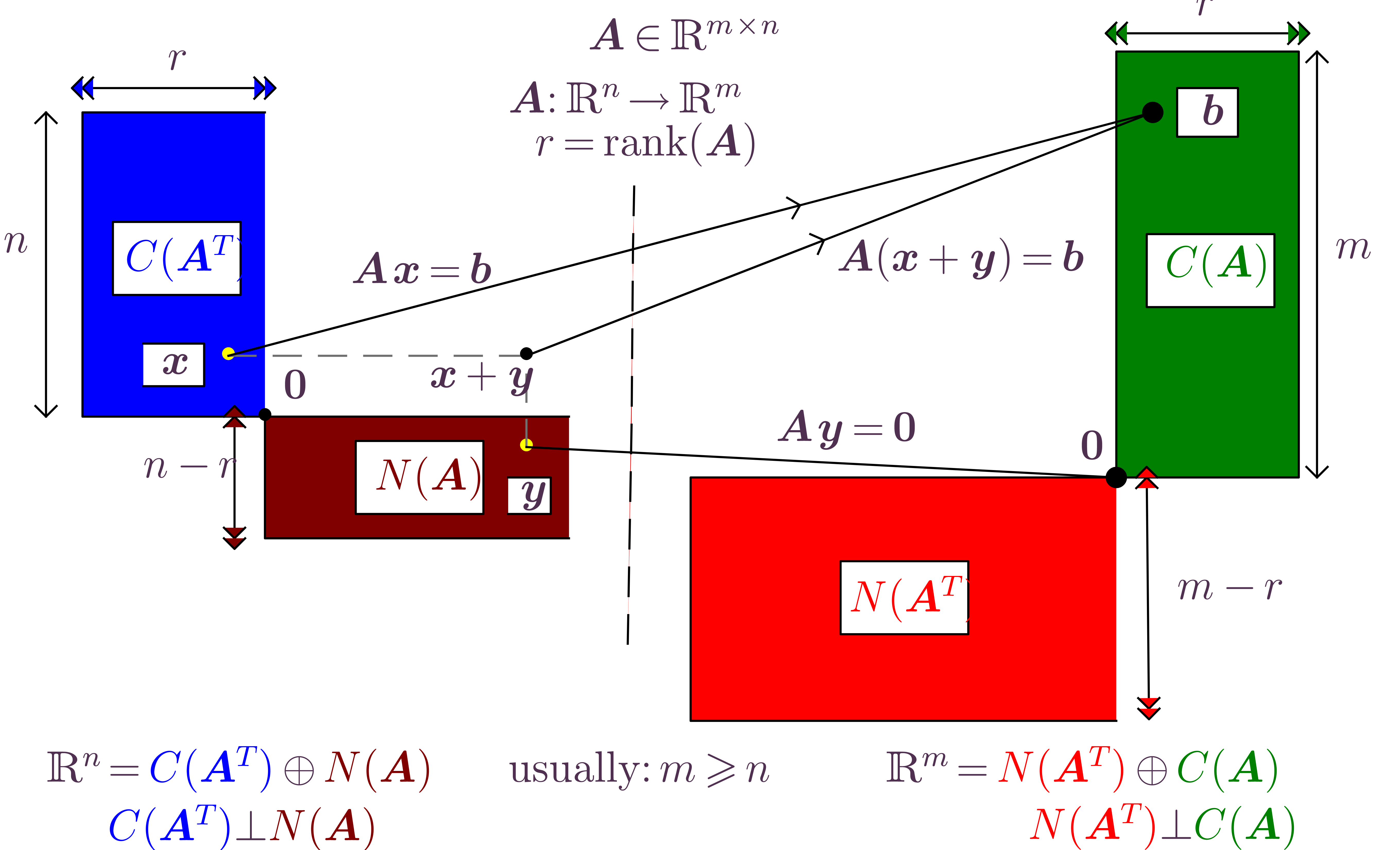
• Linear system review

• Nonlinear systems of equations

• Gradient descent methods - an introduction

• Newton and quasi-Newton methods - an introduction

Linear systems review

• $𝑨𝒙=𝒃$, $𝑨\in {ℝ}^{m\times n}$, $𝒙\in {ℝ}^n$, $𝒃\in {ℝ}^m$ a linear system of $m$ equations in $n$ unknowns. Solutions characterized by fundamental theorem of linear algebra

Nonlinear systems

• No result available comparable to FTLA

• General form of a nonlinear system $𝑭:{ℝ}^n\to {ℝ}^m$, $𝑭\left(𝒙\right)=𝟎$

  ${\displaystyle 𝑭\left(𝒙\right)=\left[\begin{array}{l}{f}_1(x_1,\dots ,x_n)\\ ⋮\\ f_m(x_1,\dots ,x_n)\end{array}\right]=𝟎}$

• Consider $m=n$ case. Examples:

  1. $x_1+x_2=1$, $\tan \left(x_1\right)+\tan \left(x_2\right)=1.10693$

  2. $\sin \left(x_1\right)+\sin \left(x_2\right)=0.954061$, $e^{x_1}-e^{x_2}=0.330294$

  3. $x_1^2+x_2^2=0.52$, $x_1^3+x_2^3=0.28$$$

• Approaches:

  • transform into an “easier” equivalent problem

  • introduce approximant $𝑮$ of $𝑭$, $𝑭\cong 𝑮$

Transformations based on norms

To solve $𝑭\left(𝒙\right)=𝟎$ use norm properties and restate problem as $||𝑭\left(𝒙\right)||=0$

Consider 2-norm and define

${\displaystyle g\left(𝒙\right)={||𝑭\left(𝒙\right)||}_2^2=\sum _{i=1}^n{f}_i^2\left(𝒙\right)}$

• $g$ is positive semi-definite: $\forall 𝒙,g\left(𝒙\right)⩾0$ and $g\left(𝒙\right)=0$ iff $𝑭\left(𝒙\right)=𝟎$

• $g$ is convex in some neighborhood of a root $𝒙$: $\exists \epsilon >0$ such that $\forall 𝒚$, $||𝒙-𝒚||⩽\epsilon$

  ${\displaystyle 𝑯\left(𝒚\right)=\left[\begin{array}{llll}\frac{{\partial }^{2}g}{\partial x_1^2}& \frac{{\partial }^{2}g}{\partial x_1\partial x_2}& \dots & \frac{{\partial }^{2}g}{\partial x_1\partial x_n}\\ & \frac{{\partial }^{2}g}{\partial x_2^2}& \dots & \frac{{\partial }^{2}g}{\partial x_2\partial x_n}\\ & & \ddots & \\ & & & \frac{{\partial }^{2}g}{\partial x_n^2}\end{array}\right],𝑯={𝑯}^T}$

  $𝑯$ is positive semi-definite, $\forall 𝒖\in {ℝ}^n$, ${𝒖}^T𝑯𝒖⩾0$, $𝑯$ has positive eigenvalues.

Gradient descent methods

• Recall, for $g:{ℝ}^n\to ℝ$, $\mathrm{grad}g=\nabla g$ is the vector indicating direction of most rapid increase of $g$

• Example: Rosenbrock function $g(x,y)={(1-x)}^2+100{(y-x^2)}^2$

  Figure 1. The Rosenbrock function

Newton method

• Instead of $𝑭\left(𝒙\right)=𝟎$ solve $𝑮\left(𝒙\right)=𝟎$ with $𝑭\cong 𝑮$, $𝑮$ linear approximant

• Linear approximant = Taylor polynomial of degree $m=1$

  ${\displaystyle 𝑷\left(𝒕\right)=𝑭\left({𝒙}_n\right)+{𝑭}^{\text{'}}\left({𝒙}_n\right)(𝒕-{𝒙}_n)}$

• Find next term in approximation sequence ${\left\{{𝒙}_n\right\}}_{n\in \mathbb{N}}$ by setting $𝑷\left({𝒙}_{n+1}\right)=𝟎\Rightarrow$

  ${\displaystyle 𝑭\left({𝒙}_n\right)+{𝑭}^{\text{'}}\left({𝒙}_n\right)({𝒙}_{n+1}-{𝒙}_n)=0\Rightarrow }$ ${\displaystyle {𝑭}^{\text{'}}\left({𝒙}_n\right)({𝒙}_{n+1}-{𝒙}_n)=-𝑭\left({𝒙}_n\right)}$

  a linear system

• As in the scalar case Newton's method is second-order convergent near the root

• Difficuly: computation of Jacobian ${𝑭}^{\text{'}}\left({𝒙}_n\right)\in {ℝ}^{n\times n}$ at each iteration

Quasi-Newton methods

• Recall that secant did not require derivatives

  ${\displaystyle \begin{array}{lll}\mathrm{replace}{x}_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\text{'}}\left(x_n\right)}& \mathrm{by}& x_{n+1}=x_n-\frac{f\left(x_n\right)}{f\left(x_n\right)-f\left(x_{n-1}\right)}(x_n-x_{n-1})\end{array}}$

• Try similar approach for $𝑭:{ℝ}^n\to {ℝ}^m$, $𝑭\left(𝒙\right)=𝟎$.

  ${\displaystyle \begin{array}{lll}\mathrm{replace}{𝒙}_{n+1}={𝒙}_n-{\left[{𝑭}^{\text{'}}\left({𝒙}_n\right)\right]}^{-1}𝑭\left({𝒙}_n\right)& \mathrm{by}& {𝒙}_{n+1}={𝒙}_n-{𝑩}_n^{-1}𝑭\left({𝒙}_n\right)\end{array}}$

• ${𝑩}_n$ is an approximation of the Jacobian ${𝑭}^{\text{'}}\left({𝒙}_n\right)$, updated at each step

• At iteration $n$ solve ${𝑩}_n{𝒔}_n=-𝑭\left({𝒙}_n\right)$, ${𝒔}_n={𝒙}_{n+1}-{𝒙}_n$

• How to construct ${𝑩}_{n+1}$? Mimic secant property $f^{\text{'}}\left(\xi \right)(b-a)=f\left(b\right)-f\left(a\right)$

  ${\displaystyle {𝑩}_{n+1}{𝒔}_n={𝒚}_n=𝑭\left({𝒙}_{n+1}\right)-𝑭\left({𝒙}_n\right)}$

  (1)

  • secant property is obtained along the direction of the most recent update

  • ${𝑩}_{n+1}$ has $n^2$ components, (1) specifies only $n$ equations

Broyden methods

• Determine $n^2$ components of ${𝑩}_{n+1}$ by imposing it be close to ${𝑩}_n$

  ${\displaystyle {min}_{{𝑩}_{n+1}}||{𝑩}_{n+1}-{𝑩}_n||}$

• Choosing the 2-norm, the above minimization problem has solution

  ${\displaystyle {𝑩}_{n+1}={𝑩}_n+\frac{({𝒚}_n-{𝑩}_n{𝒔}_n){𝒔}_n^T}{{𝒔}_n^T{𝒔}_n}}$