Solve the problems for your appropriate course track. Problems probe
understanding of the course concepts. Formulate your answers clearly and
cogently. Sketch out an approach on scratch paper first. Then briefly
transcribe the approach to the answer you turn in, followed by
appropriate calculations and conclusions, within allotted time. Use
concise, complete English sentences in the description of your approach.
Each question is meant to be completely answered and transcribed from
proof to final copy within thirty minutes. Concentrate foremost on clear
exposition of the concept underlying your approach.
-
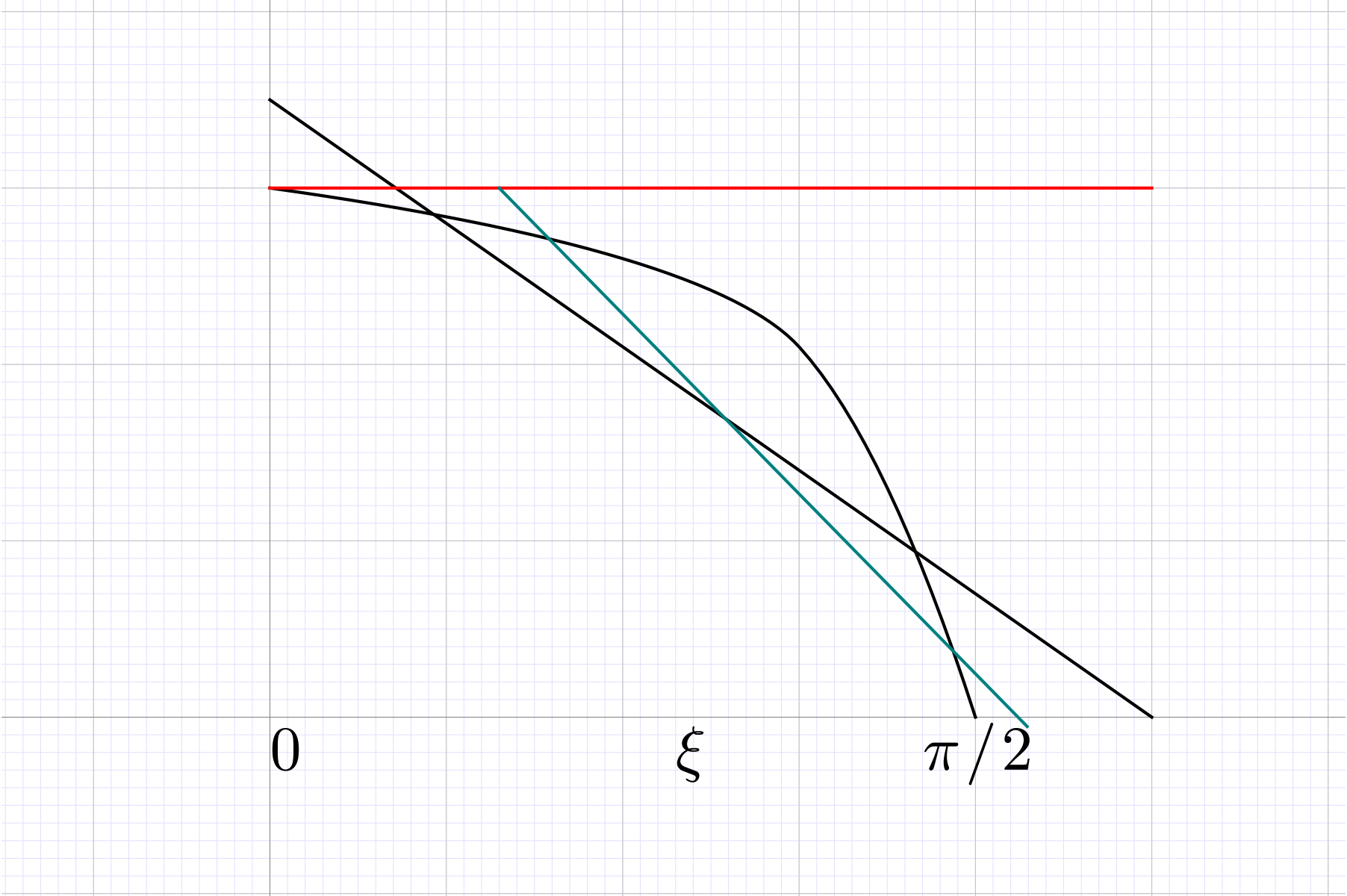
Consider the solution to
where is a first-degree polynomial. Is
an acceptable approximation of
over the interval ? If not, is there a restriction of to a subinterval that is an acceptable
approximation?
Solution. Per equi-oscillation theorem the error ,
would change sign three times over interval , at 0, ,
where is some intermediate point
.
This implies ,
hence , an
inadmissable value for cosine. An inf-norm approximant
can be constructed on some interval such that .
-
Determine the quadrature nodes
such that
has maximal order of accuracy.
Solution. The quadrature error
has minimal order for Gauss-Laguerre quadrature with scalar product
The quadrature nodes are roots of
obtained by orthogonalization of . Carry out Gram-Schmidt.
-
0
-
-
1
-
,
-
2
-
,
Roots of are
the same as of ,
hence the quadrature nodes are at
or in terms of
The weights are determined by imposing moment conditions for
-
For what values is the matrix
positive definite?
Solution. is positive definite if
for any ,
,
under which condition is symmetric
positive definite, and admits an orthogonal diagonalization
hence ,
with ,
and would need to have positive
eigenvalues for it to be positive definite. The eigenvalue problem
is
and is an eigenvalue if the
homogeneous system admits a non-trivial solution, or is a root of
the characteristic polynomial
Since
is of rank 1,
is a double eigenvalue
is s.p.d. if
and
The more restrictive condition is .
-
Compute the first three significant digits of eigenvalue of
Solution. Apply inverse power iteration with shift ,
from starting vector
Compute Raleigh quotient to obtain next approximant
of eigenvalue
and continue procedure to convergence.
-
Reduce the matrix above to lower
triangular form by a Givens rotation.
Solution. Only one rotation has to be applied in order to eliminate
element 1,3
with determined from
-
Determine the eigenvalues, determinant, and singular values of a
Householder reflector.
Solution. A Householder reflector
is an orthogonal matrix hence eigenvalues are ,
determinant is ,
and singular values are all .
-
Construct a second-order, centered discretization of the Laplacian
operator
on a Cartesian grid ,
,
,
.
Assume .
Express the discretization as a matrix
acting on the vector
Present an efficient algorithm to orthonormalize ,
i.e., compute .
Solution. The second-order centered derivative approximation is
The Laplacian at is approximated by
with a penta-diagonal matrix
Given that is sparse, the most
efficient
factorization is through Givens rotators to eliminate element
-
Prove that the eigenvalues of a Hermitian matrix are real. Prove
that the eigenvalues of a skew-Hermitian matrix are pure imaginary.
Solution. Take adjoint of
Multiply first on left by ,
second on right by and obtain
Since
it results that ,
hence is real. Similar proof for
skew-hermitian case
-
Find a two-point Gaussian quadrature for the integral
Derive the error expression, its leading order, and how it scales
with as .
Solution. Upon rescaling
See Track 1 for Gauss-Laguerre quadrature, and apply.
-
Determine the values
such that
is a cubic spline with knots ,
,
and .
Determine such is a minimum.
Solution. At the common node (knot)
impose continuity in function and first two derivatives
Compute
and impose
to determine .