This homework serves as an introduction to number approximation techniques and a familiarization with homework drafting and submission procedures. No grade points are awarded, but comments on proper assignment drafting are returned.

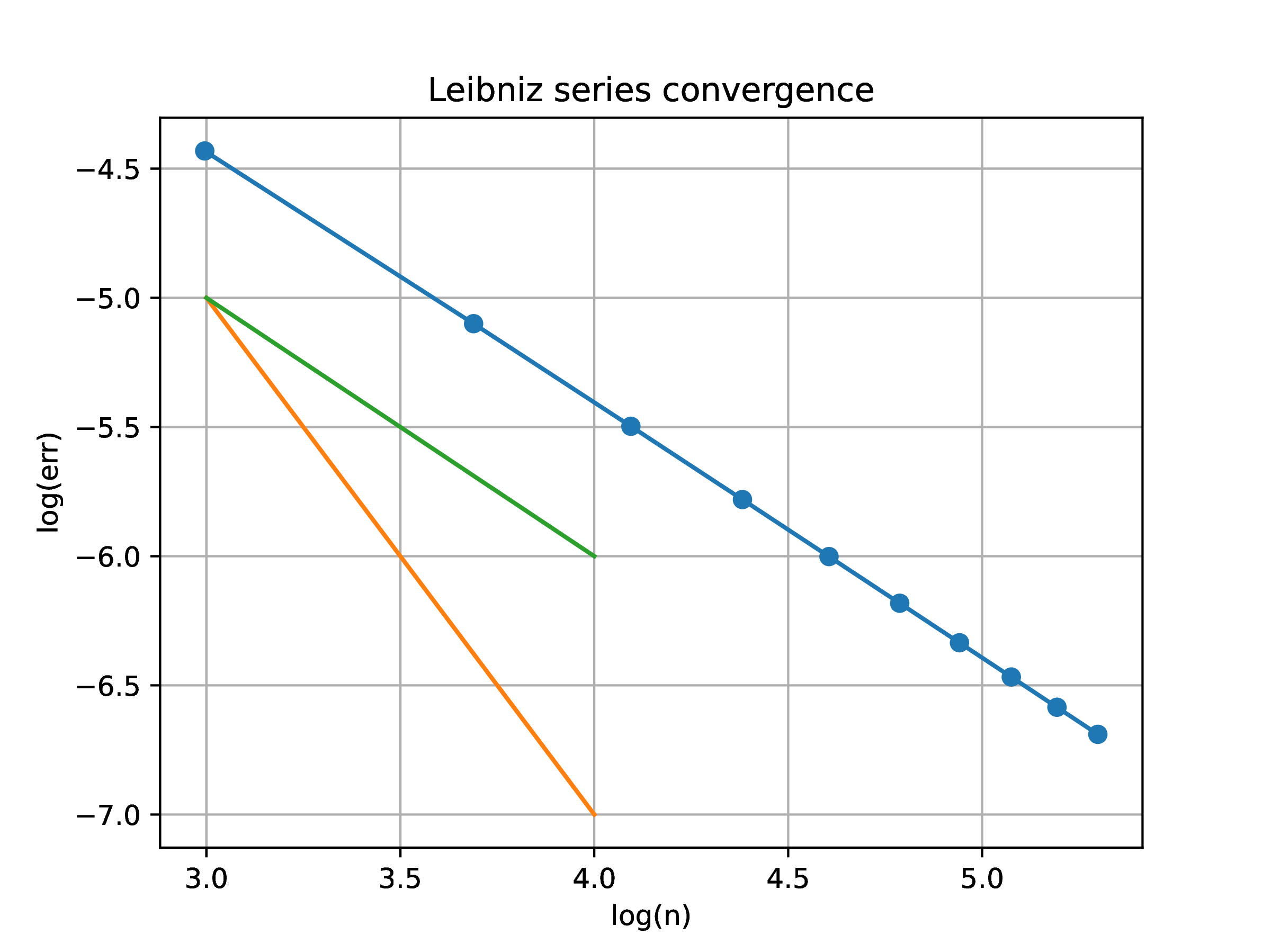
1. Construct a convergence plot in logarithmic coordinates of the Stern continued fraction

   ${\displaystyle \frac{\pi }{2}=1-}$

   Identify the terms in the general expression of a continued fraction

   ${\displaystyle F_n=b_0+\stackrel{n}{\underset{k=1}{\text{K}}}\frac{a_k}{b_k}.}$

   Compare with the additive approximation of the Leibniz series

   ${\displaystyle \frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\dots .,}$

   Estimate the rate and order of convergence for both approximations.

   Solution. (Extend the figure template below of the Leibniz approximation of $\pi /2$ to include the Stern continued fraction)

   $\circ$

   Figure 1. Convergence of Leibniz series

   ∴	N=200; n=20:20:N;

   ∴	function Leibniz(n) k=0:n sum((-1).^k ./ (2*k.+1)) end;

   ∴	err=log.(abs.(Leibniz.(n) .- π/4));

   ∴	clf(); plot(log.(n),err,"-o"); xlabel("log(n)"); ylabel("log(err)"); title("Leibniz series convergence"); grid("on"); plot([3,4],[-5,-7],"-"); plot([3,4],[-5,-6],"-");

   ∴	savefig(homedir()*"/courses/MATH661/images/H01Fig01.eps")

   ∴

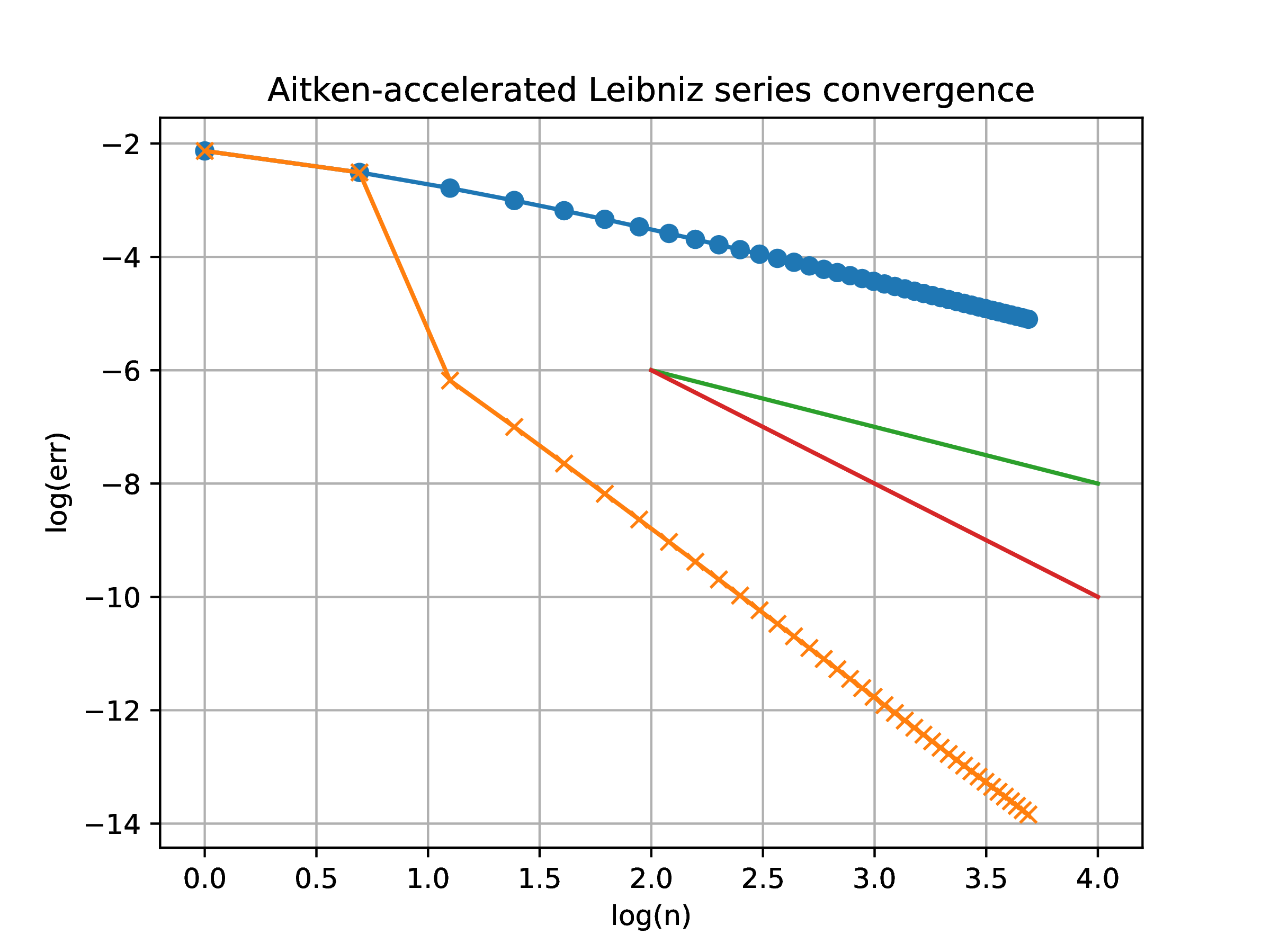
2. Apply convergence acceleration to both the above approximations involving $\pi$. Construct the convergence plot of the accelerated sequences, and estimate the new rate and order of convergence.

   Solution. (Again, feel free to modify the template below. Be careful: the Aitken formulas are valid for accelerating linear convergence. You must identify the appropriate order of convergence in Q1.)

   $\circ$

   Figure 2. Convergence of Aitken acceleration of Leibniz series

   ∴	N=40; n=1:N; L=Leibniz.(n); A=copy(L);

   ∴	for n=3:N ΔL = L[n] - L[n-1] Δ2L = L[n] - 2*L[n-1] + L[n-2] A[n] = L[n] - ΔL^2/Δ2L end

   ∴	errL=log.(abs.(L .- π/4)); errA=log.(abs.(A .- π/4));

   ∴	clf(); plot(log.(n),errL,"-o"); plot(log.(n),errA,"-x"); xlabel("log(n)"); ylabel("log(err)"); title("Aitken-accelerated Leibniz series convergence"); grid("on"); plot([2,4],[-6,-8],"-"); plot([2,4],[-6,-10],"-");

   ∴	savefig(homedir()*"/courses/MATH661/images/H01Fig02.eps")

   ∴

3. Completely state the mathematical problem of taking the $n^{\mathrm{th}}$ root of a positive real, $n\in \mathbb{N}$. Find the absolute and relative condition numbers.

   Solution.

4. Completely state the mathematical problem of finding the roots of the cubic polynomial $p\left(x\right)=x^3+px+q$, using the Cardano [2] formula. Find the absolute and relative condition numbers.

   Solution.

5. Completely state the mathematical problem of solving the initial value problem for an ordinary differential equation of first order. Use Lyapunov exponents [1] to find the absolute condition number.

   Solution.

Bibliography