Posted: 08/30/21

Due: 09/08/21, 11:55PM

1Track 1

1. Implement the classical and modified Gram-Schmidt algorithms to compute $𝑸𝑹=\mathrm{qr}\left(𝑨\right)$. Test orthogonality of $𝑸$ for $𝑨=\mathrm{randn}(m,m)$, $m=20k$, $k=1,2,\dots ,5$.

2. Generate point clouds that conform to two columns of your choice from Fig. 1. Compute the associated correlation matrix $𝑪$ and superimpose on the plots the columns of $𝑸$ from the orthogonal decomposition $𝑪=𝑸𝑹$ obtained through the modified Gram-Schmidt algorithm

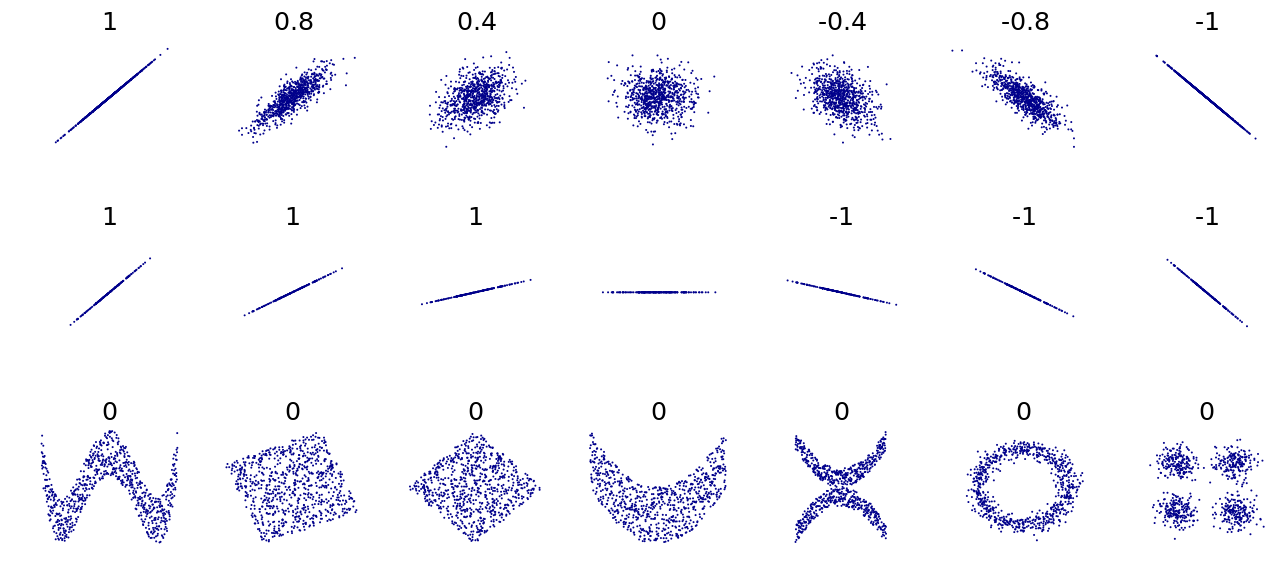   Figure 1. Point clouds with associated Pearson correlation coefficients. See Wikipedia: Correlation

3. Construct families of curves equidistant from the $x_1=0$ and $x_2=0$ axes in the plane using the $𝑨-$norm

   ${\displaystyle ||𝒙||={({𝒙}^T{𝑨}^T𝑨𝒙)}^{1/2}}$

   with $𝑨\in {ℝ}^{2\times 2}$ of full rank of your choice that is not diagonal.

2Track 2

1. Prove the Hölder inequality: for $p,q>1$, $1/p+1/q=1$,

   ${\displaystyle \sum _{i=1}^m|x_i{y}_i|⩽{\left(\sum _{i=1}^m{\left|x_i\right|}^p\right)}^{1/p}{\left(\sum _{i=1}^m{\left|y_i\right|}^q\right)}^{1/q}.}$

2. Prove the Minkowski inequality: for $p⩾1$,

   ${\displaystyle {\left(\sum _{i=1}^m{|x_i+y_i|}^p\right)}^{1/p}⩽{\left(\sum _{i=1}^m{\left|x_i\right|}^p\right)}^{1/p}+{\left(\sum _{i=1}^m{\left|y_i\right|}^p\right)}^{1/p}.}$

3. Prove the parallelogram identity

   ${\displaystyle {||𝒙+𝒚||}^2+{||𝒙-𝒚||}^2=2({||𝒙||}^2+{||𝒚||}^2),}$

   for $𝒙,𝒚\in {ℂ}^m$, with $||||$ denoting the 2-norm.

4. Consider $𝑨\in {ℂ}^{m\times m}$, $C\left(𝑨\right)={ℂ}^m$. Prove that

   ${\displaystyle {({𝒙}^{\ast }{𝑨}^{\ast }𝑨𝒙)}^{1/2}}$

   is a norm.

5. Compute the components of the saw-tooth function $f\left(t\right)=f(t+2\pi )$, $f\left(t\right)=t$ for $-\pi <t<\pi$, on the Fourier basis set

   ${\displaystyle \{\frac{1}{\sqrt{2\pi }},\frac{\cos t}{\sqrt{\pi }},\frac{\sin t}{\sqrt{\pi }},\dots ,\frac{\cos kt}{\sqrt{\pi }},\frac{\sin kt}{\sqrt{\pi }},\dots ,\frac{\cos nt}{\sqrt{\pi }},\frac{\sin nt}{\sqrt{\pi }}\},}$

   for $n=4^p$, $p=2,3,4,5$. Superimpose a plot of the approximants with the saw-tooth function. Solve any linear system or least squares problems that arise by $𝑸𝑹$ decomposition. Comment on the plot.

6. Construct visual representations of the Hadamard matrices ${𝑯}_m$, $m=4k+4$, $k\in \{0,1,2,\dots ,7\}$. Construct visual representations of $C\left({𝑯}_m\right)$, $N\left({𝑯}_m^{{}^T}\right)$, $C\left({𝑯}_m^T\right)$, $N\left({𝑯}_m\right)$ through the $𝑸𝑹$-decomposition of ${𝑯}_m$.