MATH661

Lecture 6: Fundamental Theorem of Linear Algebra

1.Vector Subspaces

1.1.Definitions

A central interest in scientific computation is to seek simple descriptions of complex objects. A typical situation is specifying an instance of some object of interest through an $m$ -tuple $𝒗 \in ℝ^{m}$ with large $m$ . Assuming that addition and scaling of such objects can cogently be defined, a vector space is obtained, say over the field of reals with an Euclidean distance, $E_{m}$ . Examples include for instance recordings of medical data (electroencephalograms, electrocardiograms), sound recordings, or images, for which $m$ can easily reach into the millions. A natural question to ask is whether all the $m$ real numbers are actually needed to describe the observed objects, or perhaps there is some intrinsic description that requires a much smaller number of descriptive parameters, that still preserves the useful idea of linear combination. The mathematical transcription of this idea is a vector subspace.

Definition. (Vector Subspace) . $𝒰 = (U, S, +, \cdot)$ , $U \neq \emptyset$ , is a vector subspace of vector space $𝒱 = (V, S, +, \cdot)$ over the same field of scalars S, denoted by $𝒰 \leq 𝒱$ , if $U \subseteq V$ and $\forall a, b \in S$ , $\forall 𝒖, 𝒗 \in U$ , the linear combination $a 𝒖 + b 𝒗 \in U$ .

The above states a vector subspace must be closed under linear combination, and have the same vector addition and scaling operations as the enclosing vector space. The simplest vector subspace of a vector space is the null subspace that only contains the null element, $U = {𝟎}$ . In fact any subspace must contain the null element $𝟎$ , or otherwise closure would not be verified for the particular linear combination $𝒖 + (- 𝒖) = 𝟎$ . If $U \subset V$ , then $𝒰$ is said to be a proper subspace of $𝒱$ , denoted by $𝒰 < 𝒱$ .

$•$ $\circ$ Setting $n - m$ components equal to zero in the real space $ℛ_{m}$ defines a proper subspace whose elements can be placed into a one-to-one correspondence with the vectors within $ℛ_{n}$ . For example, setting component $m$ of $𝒙 \in ℝ^{m}$ equal to zero gives $𝒙 = {[\begin{array}{ccccc} x_{1} & x_{2} & \dots & x_{m - 1} & 0 \end{array}]}^{T}$ that while not a member of $ℝ^{m - 1}$ , it is in a one-to-one relation with $𝒙^{'} = {[\begin{array}{cccc} x_{1} & x_{2} & \dots & x_{m - 1} \end{array}]}^{T} \in ℝ^{m - 1}$ . Dropping the last component of $𝒚 \in ℝ^{m}$ , $𝒚 = {[\begin{array}{ccccc} y_{1} & y_{2} & \dots & y_{m - 1} & y_{m} \end{array}]}^{T}$ gives vector $𝒚^{'} = [\begin{array}{cccc} y_{1} & y_{2} & \dots & y_{m - 1} \end{array}] \in ℝ^{m - 1}$ , but this is no longer a one-to-one correspondence since for some given $𝒚^{'}$ , the last component $y_{m}$ could take any value.

∴	m=3; x=[1; 2; 0]; xp=x[1:2]

$[\begin{array}{c} 1 \\ 2 \end{array}]$ (1)

∴	y=[1; 2; 3]; yp=y[1:2]

$[\begin{array}{c} 1 \\ 2 \end{array}]$ (2)

∴

Vector subspaces arise in decomposition or partitioning of a vector space. The converse, composition of vector spaces $𝒰 = (U, S, +, \cdot)$ , $𝒱 = (V, S, +, \cdot)$ is defined in terms of linear combination. A vector $𝒙 \in ℝ^{3}$ can be obtained as the linear combination

𝒙 = [\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}] = [\begin{array}{c} x_{1} \\ 0 \\ 0 \end{array}] + [\begin{array}{c} 0 \\ x_{2} \\ x_{3} \end{array}],

but also as

𝒙 = [\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}] = [\begin{array}{c} x_{1} \\ x_{2} - a \\ 0 \end{array}] + [\begin{array}{c} 0 \\ a \\ x_{3} \end{array}],

for some arbitrary $a \in ℝ$ . In the first case, $𝒙$ is obtained as a unique linear combination of a vector from the set $U = {{[\begin{array}{ccc} x_{1} & 0 & 0 \end{array}]}^{T} | x_{1} \in ℝ .}$ with a vector from $V = {{[\begin{array}{ccc} 0_{} & x_{2} & x_{3} \end{array}]}^{T} | x_{2}, x_{3} \in ℝ .}$ . In the second case, there is an infinity of linear combinations of a vector from $V$ with another from $W = {{[\begin{array}{ccc} x_{1} & x_{2} & 0 \end{array}]}^{T} | x_{1}, x_{2} \in ℝ .}$ to the vector $𝒙$ . This is captured by a pair of definitions to describe vector space composition.

Definition. Given two vector subspaces $𝒰 = (U, S, +, \cdot)$ , $𝒱 = (V, S, +, \cdot)$ of the space $𝒲 = (W, S, +, \cdot)$ , the sum is the vector space $𝒰 + 𝒱 = (U + V, S, +, \cdot)$ , where the sum of the two sets of vectors $U, V$ is $U + V = {𝒖 + 𝒗 | 𝒖 \in U, 𝒗 \in V}$ .

Definition. Given two vector subspaces $𝒰 = (U, S, +, \cdot)$ , $𝒱 = (V, S, +, \cdot)$ of the space $𝒲 = (W, S, +, \cdot)$ , the direct sum is the vector space $𝒰 \oplus 𝒱 = (U \oplus V, S, +, \cdot)$ , where the direct sum of the two sets of vectors $U, V$ is $U \oplus V = {𝒖 + 𝒗 | \exists! 𝒖 \in U, \exists! 𝒗 \in V}$ . (unique decomposition)

$•$ $\circ$ Since the same scalar field, vector addition, and scaling is used , it is more convenient to refer to vector space sums simply by the sum of the vector sets $U + V$ , or $U \oplus V$ , instead of specifying the full tuplet for each space. This shall be adopted henceforth to simplify the notation.

∴	u=[1; 0; 0]; v=[0; 2; 3]; vp=[0; 1; 3]; w=[1; 1; 0]; [u+v vp+w]

$[\begin{array}{cc} 1 & 1 \\ 2 & 2 \\ 3 & 3 \end{array}]$ (3)

∴

In the previous example, the essential difference between the two ways to express $𝒙 \in ℝ^{3}$ is that $U \cap V = {𝟎}$ , but $V \cap W = {{[\begin{array}{ccc} 0 & a & 0 \end{array}]}^{T} | a \in ℝ .} \neq {𝟎}$ , and in general if the zero vector is the only common element of two vector spaces then the sum of the vector spaces becomes a direct sum.In practice, the most important procedure to construct direct sums or check when an intersection of two vector subspaces reduces to the zero vector is through an inner product.

Definition. Two vector subspaces $U, V$ of the real vector space $ℝ^{m}$ are orthogonal, denoted as $U ⊥ V$ if $𝒖^{T} 𝒗 = 0$ for any $𝒖 \in U, 𝒗 \in V$ .

Definition. Two vector subspaces U,V of $U + V$ are orthogonal complements, denoted $U = V^{⊥}$ , $V = U^{⊥}$ if they are orthogonal subspaces, $U ⊥ V$ , and $U \cap V = {𝟎}$ , i.e., the null vector is the only common element of both subspaces.

The above concept of orthogonality can be extended to other vector subspaces, such as spaces of functions. It can also be extended to other choices of an inner product, in which case the term conjugate vector spaces is sometimes used. The concepts of sum and direct sum of vector spaces used linear combinations of the form $𝒖 + 𝒗$ . This notion can be extended to arbitrary linear combinations.

Definition. In vector space $𝒱 = (V, S, +, \cdot)$ , the span of vectors $𝒂_{1}, 𝒂_{2}, \dots, 𝒂_{n} \in V,$ is the set of vectors reachable by linear combination

$span {𝒂_{1}, 𝒂_{2}, \dots, 𝒂_{n}} = {𝒃 \in V | \exists x_{1}, \dots, x_{n} \in S such that 𝒃 = x_{1} 𝒂_{1} + \dots + x_{n} 𝒂_{n}} .$

Note that for real vector spaces a member of the span of the vectors ${𝒂_{1}, 𝒂_{2}, \dots, 𝒂_{n}}$ is the vector $𝒃$ obtained from the matrix vector multiplication

𝒃 = 𝑨 𝒙 = [\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}] [\begin{array}{c} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{array}] .

From the above, the span is a subset of the co-domain of the linear mapping $𝒇 (𝒙) = 𝑨 𝒙$ .

1.2.Vector subspaces of a linear mapping

The wide-ranging utility of linear algebra results from a complete characterization of the behavior of a linear mapping between vector spaces $𝒇 : U \to V$ , $𝒇 (a 𝒖 + b 𝒗) = a 𝒇 (𝒖) + b 𝒇 (𝒗)$ . For some given linear mapping the questions that arise are:

Can any vector within $V$ be obtained by evaluation of $𝒇$ ?
Is there a single way that a vector within $V$ can be obtained by evaluation of $𝒇$ ?

Linear mappings between real vector spaces $𝒇 : ℝ^{n} \to ℝ^{m}$ , have been seen to be completely specified by a matrix $𝑨 \in ℝ^{m \times n}$ . It is common to frame the above questions about the behavior of the linear mapping $𝒇 (𝒙) = 𝑨 𝒙$ through sets associated with the matrix $𝑨$ . To frame an answer to the first question, a set of reachable vectors is first defined.

Definition. The column space (or range) of matrix $𝑨 \in ℝ^{m \times n}$ is the set of vectors reachable by linear combination of the matrix column vectors

$C (𝑨) = range (𝑨) = {𝒃 \in ℝ^{m} | \exists 𝒙 \in ℝ^{n} such that 𝒃 = 𝑨 𝒙} .$

By definition, the column space is included in the co-domain of the function $𝒇 (𝒙) = 𝑨 𝒙$ , $C (𝑨) \subseteq ℝ^{m}$ , and is readily seen to be a vector subspace of $ℝ^{m}$ . The question that arises is whether the column space is the entire co-domain $C (𝑨) = ℝ^{m}$ that would signify that any vector can be reached by linear combination. If this is not the case then the column space would be a proper subset, $C (𝑨) \subset ℝ^{m}$ , and the question is to determine what part of the co-domain cannot be reached by linear combination of columns of $𝑨$ . Consider the orthogonal complement of $C (𝑨)$ defined as the set vectors orthogonal to all of the column vectors of $𝑨$ , expressed through inner products as

𝒂_{1}^{T} 𝒚 = 0, 𝒂_{2}^{T} 𝒚 = 0, \dots, 𝒂_{n}^{T} 𝒚 = 0 .

This can be expressed more concisely through the transpose operation

𝑨 = [\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}], 𝑨^{T} 𝒚 = [\begin{array}{c} 𝒂_{1}^{T} \\ 𝒂_{2}^{T} \\ ⋮ \\ 𝒂_{n}^{T} \end{array}] 𝒚 = [\begin{array}{c} 𝒂_{1}^{T} 𝒚 \\ 𝒂_{2}^{T} 𝒚 \\ ⋮ \\ 𝒂_{n}^{T} 𝒚 \end{array}],

and leads to the definition of a set of vectors for which $𝑨^{T} 𝒚 = 𝟎$

Definition. The left null space (or cokernel) of a matrix $𝑨 \in ℝ^{m \times n}$ is the set

$N (𝑨^{T}) = null (𝑨^{T}) = {𝒚 \in ℝ^{m} | 𝑨^{T} 𝒚 = 𝟎} .$

Note that the left null space is also a vector subspace of the co-domain of $𝒇 (𝒙) = 𝑨 𝒙$ , $N (𝑨^{T}) \subseteq ℝ^{m}$ . The above definitions suggest that both the matrix and its transpose play a role in characterizing the behavior of the linear mapping $𝒇 = 𝑨 𝒙$ , so analagous sets are define for the transpose $𝑨^{T}$ .

Definition. The row space (or corange) of a matrix $𝑨 \in ℝ^{m \times n}$ is the set

$R (𝑨) = C (𝑨^{T}) = range (𝑨^{T}) = {𝒄 \in ℝ^{n} | \exists 𝒚 \in ℝ^{m} 𝒄 = 𝑨^{T} 𝒚} \subseteq ℝ^{n}$

Definition. The null space of a matrix $𝑨 \in ℝ^{m \times n}$ is the set

$N (𝑨) = null (𝑨) = {𝒙 \in ℝ^{n} | 𝑨 𝒙 = 𝟎} \subseteq ℝ^{n}$

Examples. Consider a linear mapping $𝒇 : ℝ^{n} \to ℝ^{m}$ , defined by $𝒚 = 𝒇 (𝒙) = 𝑨 𝒙 = {[\begin{array}{ccc} y_{1} & \dots & y_{n} \end{array}]}^{T}$ , with $𝑨 \in ℝ^{m \times n}$ .

For $n = 1$ , $m = 3$ ,
$𝑨 = [\begin{array}{c} 1 \\ 0 \\ 0 \end{array}], 𝑨^{T} = [\begin{array}{ccc} 1 & 0 & 0 \end{array}],$
the column space $C (𝑨)$ is the $y_{1}$ -axis, and the left null space $N (𝑨^{T})$ is the $y_{2} y_{3}$ -plane.
For $n = 2$ , $m = 3$ ,
$𝑨 = [\begin{array}{cc} 1 & - 1 \\ 0 & 0 \\ 0 & 0 \end{array}] = [\begin{array}{cc} 𝒂_{1} & 𝒂_{2} \end{array}], 𝑨^{T} = [\begin{array}{ccc} 1 & 0 & 0 \\ - 1 & 0 & 0 \end{array}],$
the columns of $𝑨$ are colinear, $𝒂_{2} = - 𝒂_{1}$ , and the column space $C (𝑨)$ is the $y_{1}$ -axis, and the left null space $N (𝑨^{T})$ is the $y_{2} y_{3}$ -plane, as before.
For $n = 2$ , $m = 3$ ,
$𝑨 = [\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array}], 𝑨^{T} = [\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}],$
the column space $C (𝑨)$ is the $y_{1} y_{2}$ -plane, and the left null space $N (𝑨^{T})$ is the $y_{3}$ -axis.
For $n = 2$ , $m = 3$ ,
$𝑨 = [\begin{array}{cc} 1 & 1 \\ 1 & - 1 \\ 0 & 0 \end{array}], 𝑨^{T} = [\begin{array}{ccc} 1 & 1 & 0 \\ 1 & - 1 & 0 \end{array}],$
the same $C (𝑨)$ , $N (𝑨^{T})$ are obtained.
For $n = 3$ , $m = 3$ ,
$𝑨 = [\begin{array}{ccc} 1 & 1 & 3 \\ 1 & - 1 & - 1 \\ 1 & 1 & 3 \end{array}] = [\begin{array}{ccc} 𝒂_{1} & 𝒂_{2} & 𝒂_{3} \end{array}],$ $𝑨^{T} = [\begin{array}{ccc} 1 & 1 & 1 \\ 1 & - 1 & 1 \\ 3 & - 1 & 3 \end{array}] = [\begin{array}{c} 𝒂_{1}^{T} \\ 𝒂_{2}^{T} \\ 𝒂_{3}^{T} \end{array}], 𝑨^{T} 𝒚 = [\begin{array}{c} 𝒂_{1}^{T} 𝒚 \\ 𝒂_{2}^{T} 𝒚 \\ 𝒂_{3}^{T} 𝒚 \end{array}]$
since $𝒂_{3} = 𝒂_{1} + 2 𝒂_{2}$ , the orthogonality condition $𝑨^{T} 𝒚 = 𝟎$ is satisfied by vectors of form $𝒚 = [\begin{array}{ccc} a & 0 & - a \end{array}]$ , $a \in ℝ$ .

The above low dimensional examples are useful to gain initial insight into the significance of the spaces $C (𝑨), N (𝑨^{T})$ . Further appreciation can be gained by applying the same concepts to processing of images. A gray-scale image of size $p_{x}$ by $p_{y}$ pixels can be represented as a vector with $m = p_{x} p_{y}$ components, $𝒃 \in {[0, 1]}^{m} \subset ℝ^{m}$ . Even for a small image with $p_{x} = p_{y} = 128 = 2^{7}$ pixels along each direction, the vector $𝒃$ would have $m = 2^{14}$ components. An image can be specified as a linear combination of the columns of the identity matrix

𝒃 = 𝑰 𝒃 = [\begin{array}{cccc} 𝒆_{1} & 𝒆_{2} & \dots & 𝒆_{m} \end{array}] [\begin{array}{c} b_{1} \\ b_{2} \\ ⋮ \\ b_{m} \end{array}],

with $b_{i}$ the gray-level intensity in pixel $i$ . Similar to the inclined plane example from §1, an alternative description as a linear combination of another set of vectors $𝒂_{1}, \dots, 𝒂_{m}$ might be more relevant. One choice of greater utility for image processing mimics the behavior of the set ${1, \cos t, \cos 2 t, \dots, \sin t, \sin 2 t, \dots}$ that extends the second example in §1, would be for $m = 4$

𝑨 = [\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & 𝒂_{3} & 𝒂_{4} \end{array}] = [\begin{array}{cccc} 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \end{array}] .

2.Linear dependence, vector space basis and dimension

2.1.Linear dependence

For the simple scalar mapping $f : ℝ \to ℝ$ , $f (x) = a x$ , the condition $f (x) = 0$ implies either that $a = 0$ or $x = 0$ . Note that $a = 0$ can be understood as defining a zero mapping $f (x) = 0$ . Linear mappings between vector spaces, $𝒇 : U \to V$ , can exhibit different behavior, and the condtion $𝒇 (𝒙) = 𝑨 𝒙 = 𝟎$ , might be satisfied for both $𝒙 \neq 𝟎$ , and $𝑨 \neq 𝟎$ . Analogous to the scalar case, $𝑨 = 𝟎$ can be understood as defining a zero mapping, $𝒇 (𝒙) = 𝟎$ .

In vector space $𝒱 = (V, S, +, \cdot)$ , vectors $𝒖, 𝒗 \in V$ related by a scaling operation, $𝒗 = a 𝒖$ , $a \in S$ , are said to be colinear, and are considered to contain redundant data. This can be restated as $𝒗 \in span {𝒖}$ , from which it results that $span {𝒖} = span {𝒖, 𝒗}$ . Colinearity can be expressed only in terms of vector scaling, but other types of redundancy arise when also considering vector addition as expressed by the span of a vector set. Assuming that $𝒗 \notin span {𝒖}$ , then the strict inclusion relation $span {𝒖} \subset span {𝒖, 𝒗}$ holds. This strict inclusion expressed in terms of set concepts can be transcribed into an algebraic condition.

Definition. The vectors $𝒂_{1}, 𝒂_{2}, \dots, 𝒂_{n} \in V,$ are linearly dependent if there exist $n$ scalars, $x_{1}, \dots, x_{n} \in S$ , at least one of which is different from zero such that

$x_{1} 𝒂_{1} + \dots + x_{n} 𝒂_{n} = 𝟎 .$

Introducing a matrix representation of the vectors

𝑨 = [\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}]; 𝒙 = [\begin{array}{c} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{array}]

allows restating linear dependence as the existence of a non-zero vector, $\exists 𝒙 \neq 𝟎$ , such that $𝑨 𝒙 = 𝟎$ . Linear dependence can also be written as $𝑨 𝒙 = 𝟎 ⇏ 𝒙 = 𝟎$ , or that one cannot deduce from the fact that the linear mapping $𝒇 (𝒙) = 𝑨 𝒙$ attains a zero value that the argument itself is zero. The converse of this statement would be that the only way to ensure $𝑨 𝒙 = 𝟎$ is for $𝒙 = 𝟎$ , or $𝑨 𝒙 = 𝟎 \Rightarrow 𝒙 = 𝟎$ , leading to the concept of linear independence.

Definition. The vectors $𝒂_{1}, 𝒂_{2}, \dots, 𝒂_{n} \in V,$ are linearly independent if the only $n$ scalars, $x_{1}, \dots, x_{n} \in S$ , that satisfy

$x_{1} 𝒂_{1} + \dots + x_{n} 𝒂_{n} = 𝟎,$ (4)

are $x_{1} = 0$ , $x_{2} = 0$ ,…, $x_{n} = 0$ .

2.2.Basis and dimension

Vector spaces are closed under linear combination, and the span of a vector set $ℬ = {𝒂_{1}, 𝒂_{2}, \dots}$ defines a vector subspace. If the entire set of vectors can be obtained by a spanning set, $V = span ℬ$ , extending $ℬ$ by an additional element $𝒞 = ℬ \cup {𝒃}$ would be redundant since $span ℬ = span 𝒞$ . This is recognized by the concept of a basis, and also allows leads to a characterization of the size of a vector space by the cardinality of a basis set.

Definition. A set of vectors $𝒖_{1}, \dots, 𝒖_{n} \in V$ is a basis for vector space $𝒱 = (V, S, +, \cdot)$ if

$𝒖_{1}, \dots, 𝒖_{n}$ are linearly independent;

$span {𝒖_{1}, \dots, 𝒖_{n}} = V$ .

Definition. The number of vectors $𝒖_{1}, \dots, 𝒖_{n} \in V$ within a basis is the dimension of the vector space $𝒱 = (V, S, +, \cdot)$ .

2.3.Dimension of matrix spaces

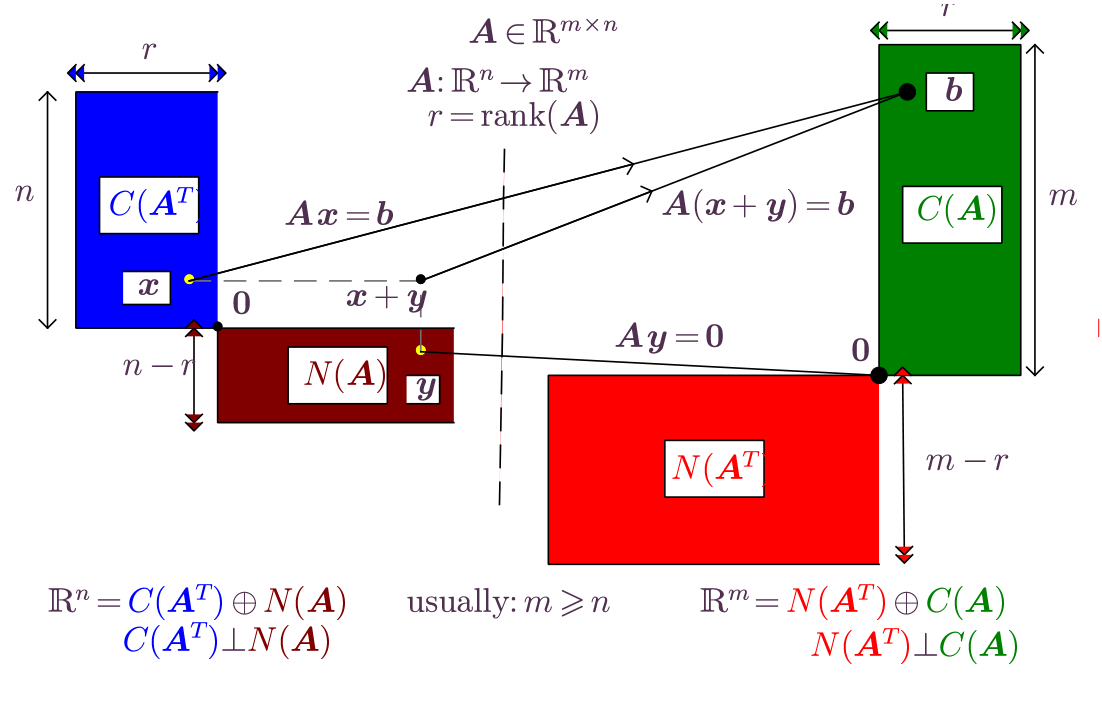
The domain and co-domain of the linear mapping $𝒇 : U \to V$ , $𝒇 (𝒙) = 𝑨 𝒙$ , are decomposed by the spaces associated with the matrix $𝑨$ . When $U = ℝ^{n}$ , $V = ℝ^{m}$ , the following vector subspaces associated with the matrix $𝑨 \in ℝ^{m \times n}$ have been defined:

$C (𝑨)$ the column space of $𝑨$
$C (𝑨^{T})$ the row space of $𝑨$
$N (𝑨)$ the null space of $𝑨$
$N (𝑨^{T})$ the left null space of $𝑨$ , or null space of $𝑨^{T}$

Definition. The rank of a matrix $𝑨 \in ℝ^{m \times n}$ is the dimension of its column space and is equal to the dimension of its row space.

Definition. The nullity of a matrix $𝑨 \in ℝ^{m \times n}$ is the dimension of its null space.

3.The FTLA

3.1.Partition of linear mapping domain and codomain

A partition of a set $S$ has been introduced as a collection of subsets $P = {S_{i} | S_{i} \subset P, S_{i} \neq \emptyset .}$ such that any given element $x \in S$ belongs to only one set in the partition. This is modified when applied to subspaces of a vector space, and a partition of a set of vectors is understood as a collection of subsets such that any vector except $𝟎$ belongs to only one member of the partition.

Linear mappings between vector spaces $𝒇 : U \to V$ can be represented by matrices $𝑨$ with columns that are images of the columns of a basis ${𝒖_{1}, 𝒖_{2}, \dots}$ of $U$

𝑨 = [\begin{array}{ccc} 𝒇 (𝒖_{1}) & 𝒇 (𝒖_{2}) & \dots \end{array}] .

Consider the case of real finite-dimensional domain and co-domain, $𝒇 : ℝ^{n} \to ℝ^{m}$ , in which case $𝑨 \in ℝ^{m \times n}$ ,

𝑨 = [\begin{array}{cccc} 𝒇 (𝒆_{1}) & 𝒇 (𝒆_{2}) & \dots & 𝒇 (𝒆_{n}) \end{array}] = [\begin{array}{cccc} 𝒂_{1} & 𝒂_{2} & \dots & 𝒂_{n} \end{array}] .

$•$ $\circ$ Example 1. Rotation by $θ$ in $ℝ^{2}$ is obtained from

𝒇 (𝒆_{1}) = [\begin{array}{l} \cos θ \\ \sin θ \end{array}], f (𝒆_{2}) = [\begin{array}{l} - \sin θ \\ \cos θ \end{array}]

leading to

𝑨 = [\begin{array}{ll} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array}] .

∴	n=15; θ=2*π/n; c=cos(θ); s=sin(θ); A=[c -s; s c];

∴	v=[1; 0]; x=[0]; y=[0];

∴	for k=0:n global x,y,v,A x=[x v[1] 0]; y=[y v[2] 0] v = A*v end

∴	clf(); plot(x',y'); axis("equal");

∴

The column space of $𝑨$ is a vector subspace of the codomain, $C (𝑨) \leq ℝ^{m}$ , but according to the definition of dimension if $n < m$ there remain non-zero vectors within the codomain that are outside the range of $𝑨$ ,

n < m \Rightarrow \exists 𝒗 \in ℝ^{m}, 𝒗 \neq 𝟎, 𝒗 \notin C (𝑨) .

All of the non-zero vectors in $N (𝑨^{T})$ , namely the set of vectors orthogonal to all columns in $𝑨$ fall into this category. The above considerations can be stated as

\begin{array}{cccc} C (𝑨) \leq ℝ^{m}, & N (𝑨^{T}) \leq ℝ^{m}, & C (𝑨) ⊥ N (𝑨^{T}) & C (𝑨) + N (𝑨^{T}) \leq ℝ^{m} \end{array} .

The question that arises is whether there remain any non-zero vectors in the codomain that are not part of $C (𝑨)$ or $N (𝑨^{T})$ . The fundamental theorem of linear algebra states that there no such vectors, that $C (𝑨)$ is the orthogonal complement of $N (𝑨^{T})$ , and their direct sum covers the entire codomain $C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ .

Lemma 2. Let $𝒰, 𝒱$ , be subspaces of vector space $𝒲$ . Then $𝒲 = 𝒰 \oplus 𝒱$ if and only if

$𝒲 = 𝒰 + 𝒱$ , and

$𝒰 \cap 𝒱 = {𝟎}$ .

Proof. $𝒲 = 𝒰 \oplus 𝒱 \Rightarrow 𝒲 = 𝒰 + 𝒱$ by definition of direct sum, sum of vector subspaces. To prove that $𝒲 = 𝒰 \oplus 𝒱 \Rightarrow 𝒰 \cap 𝒱 = {𝟎}$ , consider $𝒘 \in 𝒰 \cap 𝒱$ . Since $𝒘 \in 𝒰$ and $𝒘 \in 𝒱$ write

$\begin{array}{llll} 𝒘 = 𝒘 + 𝟎 & (𝒘 \in 𝒰, 𝟎 \in 𝒱), & 𝒘 = 𝟎 + 𝒘 & (𝟎 \in 𝒰, 𝒘 \in 𝒱), \end{array}$

and since expression $𝒘 = 𝒖 + 𝒗$ is unique, it results that $𝒘 = 𝟎$ . Now assume (i),(ii) and establish an unique decomposition. Assume there might be two decompositions of $𝒘 \in 𝒲$ , $𝒘 = 𝒖_{1} + 𝒗_{1}$ , $𝒘 = 𝒖_{2} + 𝒗_{2}$ , with $𝒖_{1}, 𝒖_{2} \in 𝒰$ , $𝒗_{1}, 𝒗_{2} \in 𝒱 .$ Obtain $𝒖_{1} + 𝒗_{1} = 𝒖_{2} + 𝒗_{2}$ , or $𝒙 = 𝒖_{1} - 𝒖_{2} = 𝒗_{2} - 𝒗_{1}$ . Since $𝒙 \in 𝒰$ and $𝒙 \in 𝒱$ it results that $𝒙 = 𝟎$ , and $𝒖_{1} = 𝒖_{2}$ , $𝒗_{1} = 𝒗_{2}$ , i.e., the decomposition is unique. $□$

In the vector space $U + V$ the subspaces $U, V$ are said to be orthogonal complements if $U ⊥ V$ , and $U \cap V = {𝟎}$ . When $U \leq ℝ^{m}$ , the orthogonal complement of $U$ is denoted as $U^{⊥}$ , $U \oplus U^{⊥} = ℝ^{m}$ .

3.2.FTLA statement

Theorem. Given the linear mapping associated with matrix $𝑨 \in ℝ^{m \times n}$ we have:

$C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ , the direct sum of the column space and left null space is the codomain of the mapping

$C (𝑨^{T}) \oplus N (𝑨) = ℝ^{n}$ , the direct sum of the row space and null space is the domain of the mapping

$C (𝑨) ⊥ N (𝑨^{T})$ and $C (𝑨) \cap N (𝑨^{T}) = {𝟎}$ , the column space is orthogonal to the left null space, and they are orthogonal complements of one another,
$\begin{array}{ll} C (𝑨) = N {(𝑨^{T})}^{⊥}, & N (𝑨^{T}) = C {(𝑨)}^{⊥} \end{array} .$

$C (𝑨^{T}) ⊥ N (𝑨)$ and $C (𝑨^{T}) \cap N (𝑨) = {𝟎}$ , the row space is orthogonal to the null space, and they are orthogonal complements of one another,
$\begin{array}{ll} C (𝑨^{T}) = N {(𝑨)}^{⊥}, & N (𝑨) = C {(𝑨^{T})}^{⊥} \end{array} .$

Figure 1. Graphical represenation of the Fundamental Theorem of Linear Algebra, Gil Strang, Amer. Math. Monthly 100, 848-855, 1993.

Consideration of equality between sets arises in proving the above theorem. A standard technique to show set equality $A = B$ , is by double inclusion, $A \subseteq B \land B \subseteq A \Rightarrow A = B$ . This is shown for the statements giving the decomposition of the codomain $ℝ^{m}$ . A similar approach can be used to decomposition of $ℝ^{n}$ .

$C (𝑨) ⊥ N (𝑨^{T})$ (column space is orthogonal to left null space).

Proof. Consider arbitrary $𝒖 \in C (𝑨), 𝒗 \in N (𝑨^{T})$ . By definition of $C (𝑨)$ , $\exists 𝒙 \in ℝ^{n}$ such that $𝒖 = 𝑨 𝒙$ , and by definition of $N (𝑨^{T})$ , $𝑨^{T} 𝒗 = 𝟎$ . Compute $𝒖^{T} 𝒗 = {(𝑨 𝒙)}^{T} 𝒗 = 𝒙^{T} 𝑨^{T} 𝒗 = 𝒙^{T} (𝑨^{T} 𝒗) = 𝒙^{T} 𝟎 = 0$ , hence $𝒖 ⊥ 𝒗$ for arbitrary $𝒖, 𝒗$ , and $C (𝑨) ⊥ N (𝑨^{T})$ . $□$
$C (𝑨) \cap N (𝑨^{T}) = {𝟎}$ ( $𝟎$ is the only vector both in $C (𝑨)$ and $N (𝑨^{T})$ ).

Proof. (By contradiction, reductio ad absurdum). Assume there might be $𝒃 \in C (𝑨)$ and $b \in N (𝑨^{T})$ and $𝒃 \neq 𝟎$ . Since $𝒃 \in C (𝑨)$ , $\exists 𝒙 \in ℝ^{n}$ such that $𝒃 = 𝑨 𝒙$ . Since $𝒃 \in N (𝑨^{T})$ , $𝑨^{T} 𝒃 = 𝑨^{T} (𝑨 𝒙) = 𝟎$ . Note that $𝒙 \neq 0$ since $𝒙 = 0 \Rightarrow 𝒃 = 0$ , contradicting assumptions. Multiply equality $𝑨^{T} 𝑨 𝒙 = 𝟎$ on left by $𝒙^{T}$ ,
$𝒙^{T} 𝑨^{T} 𝑨 𝒙 = 𝟎 \Rightarrow {(𝑨 𝒙)}^{T} (𝑨 𝒙) = 𝒃^{T} 𝒃 = {|| 𝒃 ||}^{2} = 0,$
thereby obtaining $𝒃 = 0$ , using norm property 3. Contradiction.

$□$
$C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$

Proof. (iii) and (iv) have established that $C (𝑨), N (𝑨^{T})$ are orthogonal complements
$C (𝑨) = N {(𝑨^{T})}^{⊥}, N (𝑨^{T}) = C {(𝑨)}^{⊥} .$
By Lemma 2 it results that $C (𝑨) \oplus N (𝑨^{T}) = ℝ^{m}$ . $□$

The remainder of the FTLA is established by considering $𝑩 = 𝑨^{T}$ , e.g., since it has been established in (v) that $C (𝑩) \oplus N (𝑨^{T}) = ℝ^{n}$ , replacing $𝑩 = 𝑨^{T}$ yields $C (𝑨^{T}) \oplus N (𝑨) = ℝ^{m}$ , etc.

Summary.

Vector subspaces are subsets of a vector space closed under linear combination
The simplest vector subspace is ${𝟎}$
Linear mappings are represented by matrices
Associated with matrix $𝑨 \in ℝ^{m \times n}$ that represents mapping $f : ℝ^{n} \to ℝ^{m}$ are four fundamental subspaces:
1. $C (𝑨) ⩽ ℝ^{m}$ the column space of $𝑨$ containing vectors $𝒃$ reachable by $𝑨 𝒙$ , $𝒃 = 𝑨 x$
2. $N (𝑨^{T}) ⩽ ℝ^{m}$ the left null space of $𝑨$ containing vectors $𝒚$ orthogonal to columns $𝑨$ , $𝑨^{T} 𝒚 = 0$
3. $C (𝑨^{T}) ⩽ ℝ^{n}$ the row space of $𝑨$
4. $N (𝑨) ⩽ ℝ^{n}$ the null space of $𝑨$