This homework marks your first foray into realistic scientific computation by applying concepts from linear algebra, specifically using the singular value decomposition to analyze hurricane Lee, still active at this time.

1Problem setup

1.1Image data

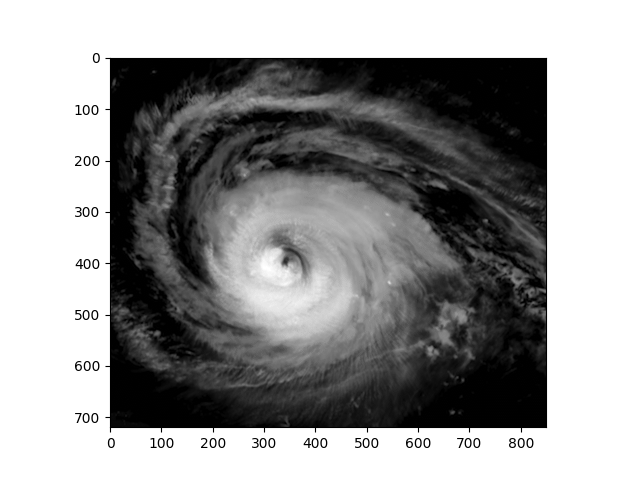
Processing of image data through the tools of linear algebra is often encountered, and in this assignment you shall work with satellite images of hurricane Lee of 2023 Season. Open the following folds and execute the code to set up your environment.

cd ~/courses/MATH661/data/weather

animate HurricaneLee.gif &

∴ 

import Pkg; Pkg.add("Images");

∴ 

Pkg.add(["FileIO","ImageIO"]);

∴ 

∴ 

using Images, FileIO, ImageIO

∴ 

∴ 

pre=homedir()*"/courses/MATH661/data/weather/";

∴ 

gif=load(pre*"HurricaneLee.gif");

∴ 

(mx,my,nf)=size(gif)

∴ 

∴ 

n=20; frame = Gray.(gif[:,:,n]);

∴ 

A = Float32.(frame); clf(); imshow(A,cmap="gray");

∴ 

hwdir=homedir()*"/courses/MATH661/homework/H03"; 

∴ 

savefig(hwdir*"/H03Fig01.png");

∴ 

∴ 

window = Gray.(gif[51:650,101:750,:]);

∴ 

data = Float32.(window); clf(); imshow(data[:,:,nf],cmap="gray");

∴ 

(nx,ny,nf) = size(data)

∴ 

Figure 1. Night-time satellite imagery of hurricane Lee. Superimposed on the familiar overall anti-cyclone pattern are small-scale features (lightning, cloud patterns in the arms). The SVD can be used to distinguish between small and large scale features.

Figure 2. Data window of a time snapshot of hurricane Lee.

1.2Computing the SVD

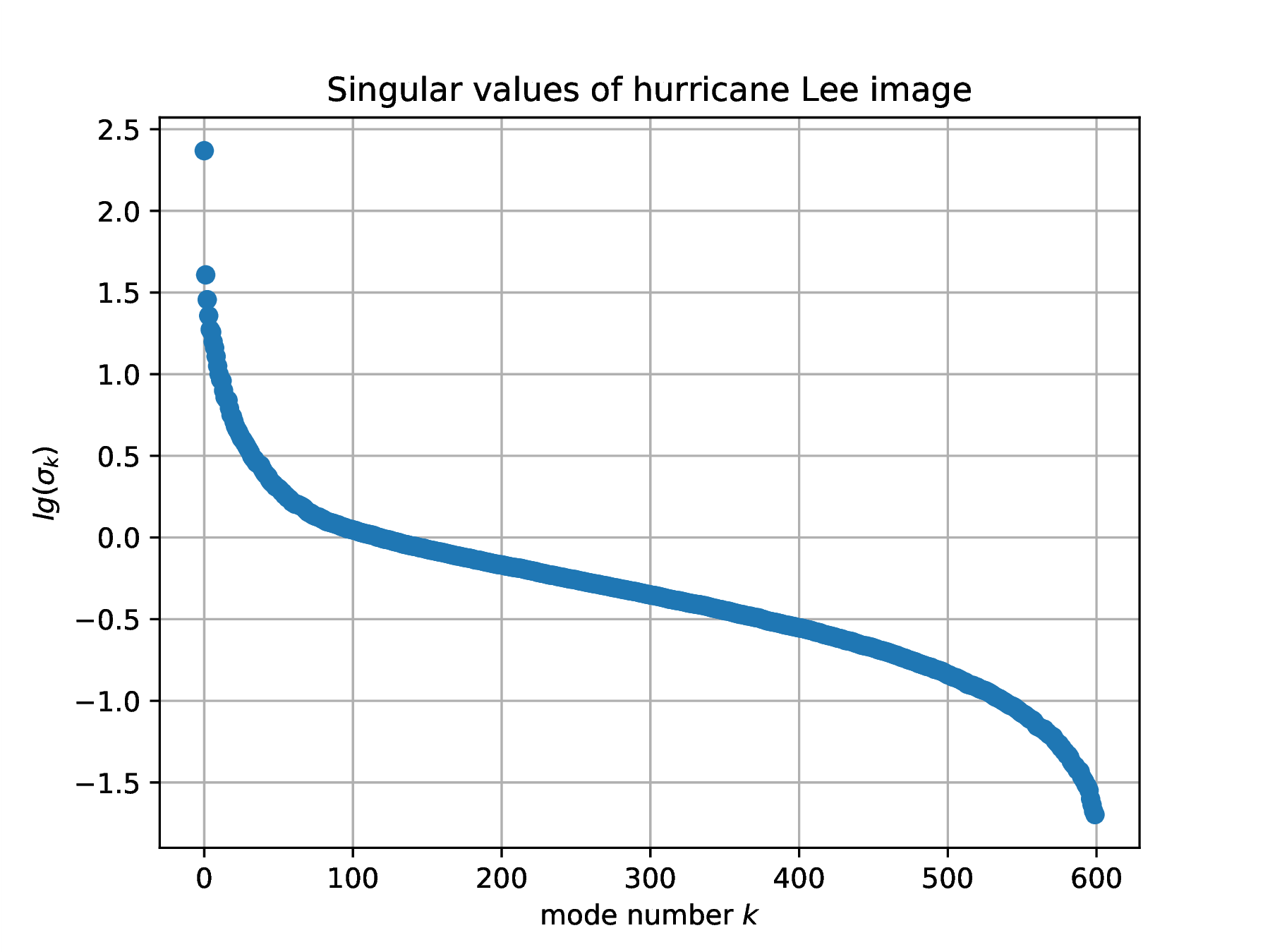
The SVD of the array of floats obtained from an image identifies correlations in gray-level intensity between pixel positions, an encoded description of weather physics. Here are the Julia instructions to compute the SVD of one frame of image data. It is instructive to plot the singular values $\Sigma =\mathrm{diag}({\sigma }_1,{\sigma }_2,\dots )$, in log coordinates.

∴ 

n=32; A=data[:,:,n]; U,S,V=svd(A);

∴ 

clf(); plot(log10.(S),"o"); xlabel(L"mode number $k$"); ylabel(L"lg(\sigma_k)");

∴ 

title("Singular values of hurricane Lee image"); grid("on");

∴ 

hwdir=homedir()*"/courses/MATH661/homework/H03"; savefig(hwdir*"/H03Fig03a.eps");

∴ 

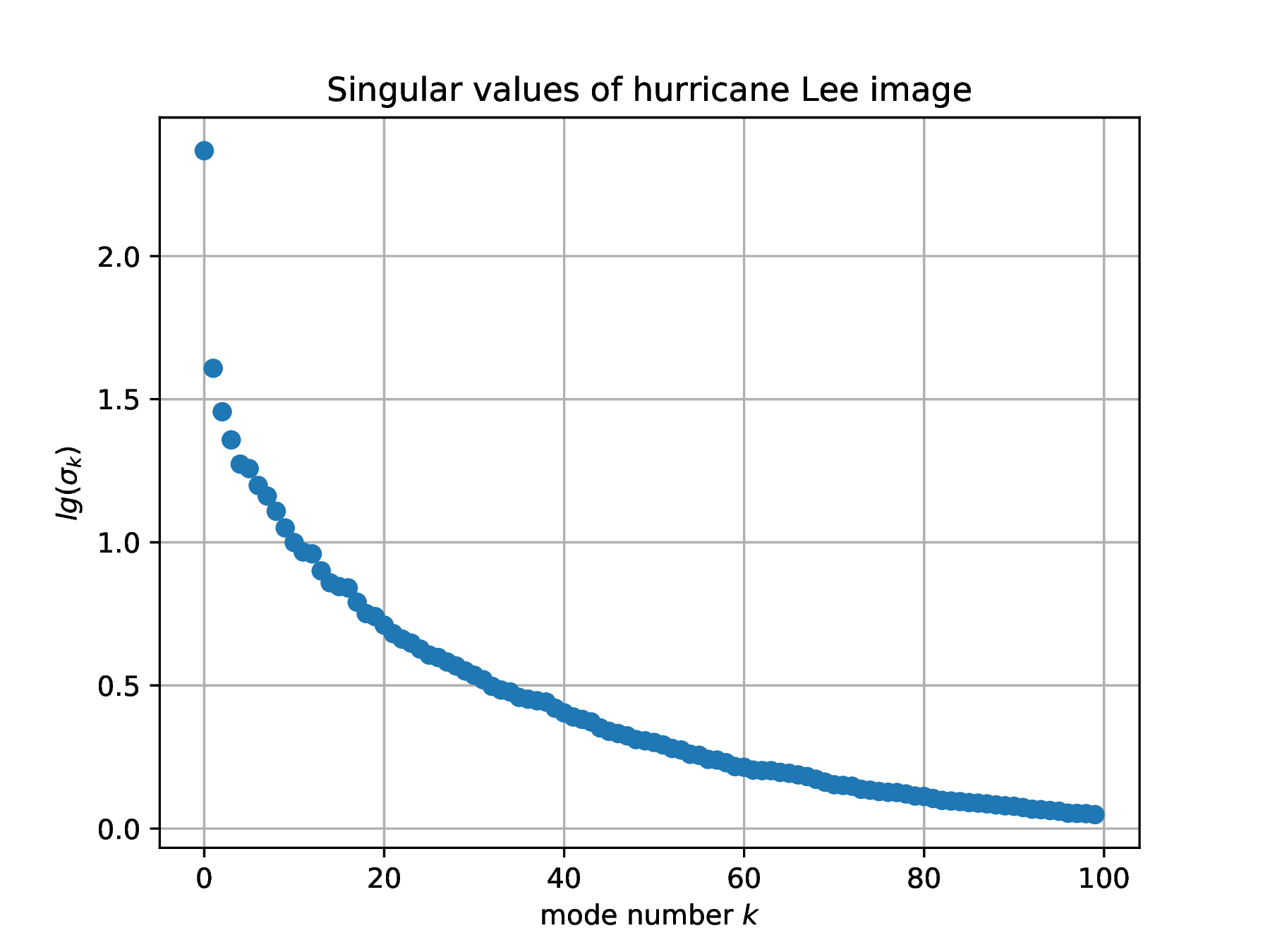
clf(); plot(log10.(S[1:100]),"o"); xlabel(L"mode number $k$"); ylabel(L"lg(\sigma_k)");

∴ 

title("Singular values of hurricane Lee image"); grid("on");

∴ 

savefig(hwdir*"/H03Fig03b.eps");

∴ 

Figure 3. The singular values of a hurricane satellite image rapidly decay from $\sim {10}^{2.5}$ to $\sim {10}^0$, a two order-of-magnitude decrease over the first 100 modes (singular vectors). This indicates considerable data compression is possible.

∴ 

function rsvd(p,q,U,S,V)
  B = S[p]*U[:,p]*V[:,p]'
  for k=p+1:q
    B = B + S[k]*U[:,k]*V[:,k]'
  end
  return B
end;

∴ 

p=1; q=12; B = rsvd(p,q,U,S,V); clf(); imshow(B,cmap="gray");

∴ 

savefig(hwdir*"/H03Fig04a.png");

∴ 

p=101; q=140; B = rsvd(p,q,U,S,V); clf(); imshow(B,cmap="gray");

∴ 

savefig(hwdir*"/H03Fig04b.png");

∴ 

Figure 4. (Left) Reconstruction of hurricane Lee image from first $q=12$ modes, showing large scale patterms. (Right) Correlated small-scale patterns obtained by sum of modes $p=101$ to $q=140$.

2Common problems (both tracks)

1. Consider large-scale weather patterns ${𝑩}_k$, ${𝑩}_{k-1}$, ${𝑩}_{k-2}$ obtained from the $p$ most significant modes from frames $k,k-1,k-2$ (i.e., different times in the past). Assuming a constant rate of change leads to the prediction

   ${\displaystyle {𝑷}_k={𝑩}_{k-1}+({𝑩}_{k-1}-{𝑩}_{k-2})}$

   (3)

   for the known large-scale weather ${𝑩}_k$. The prediction error is ${\epsilon }_{k,1}\left(p\right)={||{𝑷}_k-{𝑩}_k||}_F/{||{𝑩}_k||}_F$. Present a plot of the prediction error for various values of $p$ over the recorded hurricane data. Analyze your results to answer the question: “can overall storm evolution be predicted by linear extrapolation of past data?”

   Solution.

   $\circ$Define a function to construct prediction at time $k$ by linear extrapolation of modes from $p$ to $q$ at times $k-1,k-2$

   ∴	function LinPredict(k,p,q,data) A1 = data[:,:,k-1]; U1,S1,V1=svd(A1); B1=rsvd(p,q,U1,S1,V1) A2 = data[:,:,k-2]; U2,S2,V2=svd(A2); B2=rsvd(p,q,U2,S2,V2) P = B1 + (B1-B2) end;

   ∴	k,p,q=10,1,10; P=LinPredict(k,p,q,data); figure(1); clf(); imshow(P,cmap="gray");

   ∴

   Note the close correspondence between mathematical notation and coding.

   $\circ$Define a function to compare the coarse grained prediction and data

   ∴

   function Compare(k,p,q,data,predict) P=predict(k,p,q,data) A = data[:,:,k]; U,S,V=svd(A); B=rsvd(p,q,U,S,V) fig=figure(1,figsize=(10,4)); clf() (ax1,ax2) = fig.subplots(1,2) fig.suptitle("Comparison using modes "*string(p)*" to "*string(q)) ax1.imshow(P,cmap="gray"); ax1.set_title("Prediction") ax2.imshow(B,cmap="gray"); ax2.set_title("Data") savefig(hwdir*"/anim/frame"*lpad(string(k),4,"0")*".png") err = norm(P-B)/norm(B) end;

   ∴	Compare(10,1,10,data,LinPredict)

   $0.07692018$

   ∴	size(data)[3]

   $100$

   ∴

   The above implementation returns the prediction error and also plots the prediction and available data. The images are saved to a work directory to construct an animation.

   $\circ$Define a function to plot the prediction error over the available data

   ∴

   function ErrPlot(p,q,data,np,s) n=size(data)[3]; err=ones(n) for k=3:n err[k] = Compare(k,p,q,data,LinPredict) sleep(0.25) # Allow plot display during loop end figure(np); plot(3:n,err[3:n],s); title("Prediction error") grid("on"); xlabel("Time step"); ylabel(L"\epsilon"); savefig(hwdir*"/H03Fig06.png"); return err end;

   ∴	np=3; figure(np); clf(); err01to10=ErrPlot(1,10,data,np,".");

   ∴	err01to05=ErrPlot(1,5,data,np,"xr");

   ∴	err01to20=ErrPlot(1,20,data,np,"ok");

   ∴	figure(np); savefig(hwdir*"/H03Fig05.png");

   ∴	figure(1); Compare(40,1,5,data,LinPredict); savefig(hwdir*"/H03Fig06a.png");

   ∴	Compare(40,1,10,data,LinPredict); savefig(hwdir*"/H03Fig06b.png");

   ∴	Compare(40,1,20,data,LinPredict); savefig(hwdir*"/H03Fig06c.png");

   ∴

   Encapsulating the comparison now allows study of error evolution in time and change with respect to number of modes..

   Figure 5. Linear extrapolation error, unprocessed images: ($\times$) modes $p=1$ to $q=5$; ($•$) modes $p=1$ to $q=10$; ($•$) modes $p=1$ to $q=20$.

   Relative error (Fig. 5) between prediction and observed data increases as with increase in the number of SVD modes (Fig. 6). This might seem surprising at first glance, but the comparison is done on raw data. In almost all real-world applications additional pre/post-processing of data is needed to:

   ensure identical illumination in the two images;

   align and rotate the images to match overall features (aka “image registration”)

   determine whether pixel-by-pixel comparison is meaningful as opposed to derived measures: total cloud cover, position of center, etc.

   Bonus point project (4 points). Carry out the above operations. Of particular relevance is the recognition of overall structure in data, in this case the spiral pattern of the anti-cyclone. Think of a way to use this knowledge of the expected overall pattern to better compare predictions to data.

   Figure 6. Comparison of coarse-grained prediction with data for $5,10,20$ modes from top to bottom.

2. Repeat the above construction of an error plot for local weather patterns ${𝑪}_k,{𝑪}_{k-1},{𝑪}_{k-2}$ for lesser significance modes from $p$ to $q$, that lead to prediction

   ${\displaystyle {𝑸}_k={𝑪}_{k-1}+({𝑪}_{k-1}-{𝑪}_{k-2}).}$

   Analyze your results to answer the question: “are small-scale storm features predictable?”

   Solution. The key word in the problem statement is “repeat”. Defining purpose-specific functions is not only good coding practice, but saves time in studying similar problems. Here, the previously defined functions are simply invoked with new parameters.

   $\circ$

   Figure 7. Linear extrapolation error, unprocessed images: ($\times$) modes $p=30$ to $q=60$; ($•$) modes $p=60$ to $q=90$.

   ∴	np=3; figure(np); clf(); err30to60=ErrPlot(30,60,data,np,"xr");

   ∴	err30to60=ErrPlot(60,90,data,np,".");

   ∴	figure(np); savefig(hwdir*"/H03Fig07.png");

   ∴

   The $𝒪\left(1\right)$ relative error (Fig. 7) would at first glance indicate no predictive capability of the linear extrapolation of the fine scale structure. However the error definition is inappropriate:

   • the error measure is global while the modes reflect structure at smaller spatial scales

   • illumination and registration has not been performed.

   As in the previous case, several additional steps have to be carried out on the fine scale data in order to determine whether linear extrapolation is an efficient predictor. In particular, the smaller spatial extent has to be taken into account. A typical processing sequence would:

   • Ensure equal illumination and registration

   • Define a window of smaller size, and construct the mean and variance observed when translating the window over the entire image. This would be a data-extracted model of small-scale features of the hurricane

   • Use observed mean and variance to construct extrapolated small-scale features.

3. Repeat the above for combined large ($𝑩$) and small scale ($𝑪$) weather patterns. Experiment with different weights $u,v$ in the linear combination $u𝑩+v𝑪$, $u+v=1$.

   Solution.

   $\circ$Define a function to combine both large and small scales into a weighted average

   Note that this is a straightforward extension of the previously define LinPredict function. Indeed, this is how most scientific code is written, by building upon previous code to account for new cases.

   ∴	function wLinPredict(k,pu,qu,u,pv,qv,v,data) A1=data[:,:,k-1]; U1,S1,V1=svd(A1); B1=rsvd(pu,qu,U1,S1,V1); C1=rsvd(pv,qv,U1,S1,V1) A2=data[:,:,k-2]; U2,S2,V2=svd(A2); B2=rsvd(pu,qu,U2,S2,V2); C2=rsvd(pv,qv,U2,S2,V2) P = u*(B1 + (B1-B2)) + v*(C1 + (C1-C2)) end;

   ∴

   $\circ$Define a function to compare the combined large/small-scale prediction and data

   ∴

   function wCompare(k,pu,qu,u,pv,qv,v,data,wpredict) P=wpredict(k,pu,qu,u,pv,qv,v,data); A=data[:,:,k] err = norm(P-A)/norm(A) fig=figure(1,figsize=(10,4)); clf() (ax1,ax2) = fig.subplots(1,2) fig.suptitle("Comparison using modes "*string(pu)*" to "*string(qu)*" u="*string(u)* " and "*string(pv)*" to "*string(qv)*" v="*string(v)) ax1.imshow(P,cmap="gray"); ax1.set_title("Prediction") ax2.imshow(A,cmap="gray"); ax2.set_title("Data") savefig(hwdir*"/anim/frame"*lpad(string(k),4,"0")*".png") return err end;

   ∴	wCompare(10,1,10,0.7,30,60,0.3,data,wLinPredict)

   $0.33098787783018163$

   ∴

   The above implementation returns the prediction error and also plots the prediction and available data. The images are saved to a work directory to construct an animation.

   $\circ$Define a function to plot the prediction error over the available data

   ∴

   function wErrPlot(pu,qu,u,pv,qv,v,data,np,s) n=size(data)[3]; err=ones(n) for k=3:n err[k] = wCompare(k,pu,qu,u,pv,qv,v,data,wLinPredict) sleep(0.25) # Allow plot display during loop end figure(np); plot(3:n,err[3:n],s); title("Prediction error") grid("on"); xlabel("Time step"); ylabel(L"\epsilon"); savefig(hwdir*"/H03Fig09.png"); return err end;

   ∴

   Encapsulating the comparison now allows study of error evolution in time and change with respect to number of modes..

   $\circ$

   Figure 8. Linear extrapolation error using large and small modes

   ∴	np=3; figure(np); clf(); err=wErrPlot(1,10,0.7,30,60,0.3,data,np,".");

   ∴	figure(np); savefig(hwdir*"/H03Fig08.png");

   ∴

   ∴

4. Formula (3) expresses a degree-one in time $t$ prediction

   ${\displaystyle 𝑩\left(t\right)={𝑩}_{k-1}+(t-k+1)({𝑩}_{k-1}-{𝑩}_{k-2}),}$

   evaluated at $t=k$. Construct a quadratic prediction based upon data ${𝑩}_{k-1},{𝑩}_{k-2},{𝑩}_{k-3}$, and compare with degree-one prediction in question 1. Recall that a quadratic can be constructed from knowledge of three points. Again, experiment with various values of $k,p$.

   Solution. Consider $y\left(t\right)$ with known values $y_i=y\left(i\right)$ at $i=0,1,2$. The quadratic passing through these three points is

   ${\displaystyle y\left(t\right)=\frac{1}{2}(t-1)(t-2)y_0-t(t-2)y_1+\frac{1}{2}t(t-1)y_2,}$

   and predicts value

   ${\displaystyle y\left(3\right)=y_0-3y_1+3y_2,}$

   hence quadratic predictions are given by

   ${\displaystyle {𝑩}_k={𝑩}_{k-3}-3{𝑩}_{k-2}+3{𝑩}_{k-1}.}$

   $\circ$

   Figure 9. (Left) Errors of large scale quadratic prediction; (Right) Comparison.

   Errors for quadratic extrapolation (Fig. 9) are higher than those for linear extrapolation (Fig. 5). In addition to the errors discussed previously (illumination, registration), higher order extrapolation generally exhibits higher error (to be discussed during presentation of polynomial interpolation).

   Carrying the error computation, say for the large scale modes, is easily done using previously defined functions and a new quadratic prediction function

   ∴	function QuadPredict(k,p,q,data) A1 = data[:,:,k-1]; U1,S1,V1=svd(A1); B1=rsvd(p,q,U1,S1,V1) A2 = data[:,:,k-2]; U2,S2,V2=svd(A2); B2=rsvd(p,q,U2,S2,V2) A3 = data[:,:,k-3]; U3,S3,V3=svd(A3); B3=rsvd(p,q,U3,S3,V3) P = B3 + 3*(B1-B2) end;

   ∴

   function ErrPlot(p,q,data,np,s) n=size(data)[3]; err=ones(n) for k=4:n err[k] = Compare(k,p,q,data,QuadPredict) sleep(0.25) # Allow plot display during loop end figure(np); plot(4:n,err[4:n],s); title("Prediction error") grid("on"); xlabel("Time step"); ylabel(L"\epsilon"); savefig(hwdir*"/H03Fig09.png"); return err end;

   ∴	np=3; figure(np); clf(); err=ErrPlot(1,10,data,np,".");

   ∴

   $0.12888846$

   ∴

3Track 2 questions

Use the SVD to investigate how familiar properties for $a\in ℝ$ might extend to matrices $𝑨\in {ℝ}^{m\times m}$. For example, on the real axis adding $-a$ to $a$ results in the null element, $a-a=0$, so we say $a$ is a distance $\left|a\right|$ from zero. This easily generalizes to ${ℝ}^m$, and the minimal modification of $𝒂\in {ℝ}^m$ to obtain zero is $-𝒂$, $𝒂+(-𝒂)=𝟎$, and $𝒂$ is distance $||𝒂||$ away from zero. Consider now matrices $𝑨\in {ℝ}^{m\times m}$, with $\mathrm{rank}\left(𝑨\right)=m$. How far is this matrix from “zero”? By “zero” we shall understand a singular matrix with $\mathrm{rank}\left(𝑨\right)<m$.

All real numbers $x\in ℝ$ can be obtained as the limit of a sequence of rationals $\{p_n/q_n\}$, $p_n,q_n\in \mathbb{Z}$. We say that the rationals $\mathbb{Q}$ is a dense subset of $ℝ$. What about matrix spaces?

1. Find $𝑿$ of minimal norm such that $𝑨+𝑿$ is singular. State how far $𝑨$ is from “zero”?

   Solution. Seek insight from $m=1$ for which the problem is to find $x$ of minimal norm such that $a+x=0$. From

   ${\displaystyle 0=|a+x|⩾\left|a\right|-\left|x\right|\Rightarrow \left|x\right|⩾\left|a\right|\text{ and }0=|x+a|⩾\left|x\right|-\left|a\right|\Rightarrow \left|x\right|⩽\left|a\right|}$

   deduce that $\left|x\right|=\left|a\right|$ and the solution is $x=-a$. Recall that $||𝑨||$ (the induced 2-norm in the context of an SVD), the maximal amplication factor along any direction within ${ℝ}^m$, becomes $\left|a\right|$, interpreted as the amplification factor when $m=1$. What changes when $m>1$? There are now different amplification factors of $𝑨$ along different directions. The maximum amplification factor (i.e., the matrix norm) is given by the largest singular value

   ${\displaystyle {\sigma }_1=||𝑨||={sup}_{||𝒖||=1}||𝑨𝒖||,\text{ and }||𝑨𝒖||⩽{\sigma }_1||𝒖||.}$

   There is now also a minimal amplification factor, the smallest singular value

   ${\displaystyle {\sigma }_m={inf}_{||𝒖||=1}||𝑨𝒖||,\text{ and }||𝑨𝒖||⩾{\sigma }_m||𝒖||.}$

   The matrix $𝑨$ is singular if ${\sigma }_m=0$, stating that along at least one direction $𝒗$ the scaling factor is null, $𝑨𝒗=𝟎$, in which case $𝑿=𝟎$ is of minimal norm and trivially satisfies the problem conditions. Assume now that $𝑨$ is not singular, ${\sigma }_m>0$, and investigate the smallest amplification factor of $𝑨+𝑿$, seeking a lower bound for $||(𝑨+𝑿)𝒖||$ along some arbitrary direction $𝒖$,

   ${\displaystyle ||(𝑨+𝑿)𝒖||=||𝑨𝒖+𝑿𝒖||⩾||𝑨𝒖||-||𝑿𝒖||⩾({\sigma }_m-||𝑿||)||𝒖||.}$

   The above states that if $||𝑿||<{\sigma }_m$ then $||(𝑨+𝑿)𝒖||$>0 for $||𝒖||=1$ and $𝑨+𝑿$ is not singular. Hence, in order for $𝑨+𝑿$ to be singular the condition $||𝑿||⩾{\sigma }_m$ must hold. Use the SVD of $𝑨=𝑼𝚺{𝑽}^T$ and construct

   ${\displaystyle 𝑿=𝑼\mathrm{diag}(0,\dots ,0,-{\sigma }_m){𝑽}^T}$

   that makes the sum $𝑨+𝑿$ singular, and $||𝑿||={\sigma }_m$, the minimal allowed norm.

2. Prove that any matrix in ${ℝ}^{m\times m}$ is the limit of a sequence of matrices of full rank, i.e., the set of full-rank matrices is a dense subset of ${ℝ}^{m\times m}$.

   Solution. The SVD of $𝑨$ of rank $r$ is $𝑨=𝑼𝚺{𝑽}^T$ with $𝚺=\mathrm{diag}({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_r,0,\dots ,0)$. Define sequences ${\left\{s_n^{\left(j\right)}\right\}}_{n\in \mathbb{N}}$ such that

   ${\displaystyle {lim}_{n\to \infty }{s}_n^{\left(j\right)}={\sigma }_j,e.g.}$

   ${\displaystyle s_n^{\left(j\right)}=\frac{n+1}{n}{\sigma }_j\mathrm{for}j⩽r,s_n^{\left(j\right)}=\frac{n+1}{n^2}\mathrm{for}j>r.}$

   Then ${𝑨}_n=𝑼{𝑺}_n{𝑽}^T$ with ${𝑺}_n=\mathrm{diag}(s_n^{\left(1\right)},s_n^{\left(2\right)},\dots s_n^{\left(m\right)})$ are of full rank and ${lim}_{n\to \infty }{𝑨}_n=𝑨$.