The basic idea in linear operator approximation is to apply the exact operator to an approximation of the input. These exercises explore and reinforce this concept.

1Track 1

1. Use Taylor series expansions to verify the approximations

   ${\displaystyle f^{\text{'}}\left(t\right)\cong \frac{1}{12h}[-f(t+2h)+8f(t+h)-8f(t-h)+f(t-2h)],}$

   (1)

   ${\displaystyle f^{\text{'}}\left(t\right)\cong \frac{1}{2h}[-3f\left(t\right)+4f(t+h)-f(t+2h)].}$

   (2)

   Determine the error term. Construct the polynomial approximant $p_n\left(t\right)\cong f\left(t\right)$ whose derivative leads to the above formula. Conduct a convergence study as $h\to 0$ for $f\left(t\right)\in \{\sin (\pi t/4),e^{10t},e^{-10t}\}$ at $t_0=1$, and compare the observed order of convergence with the theoretical estimate.

   Solution. For hand computation, organize Taylor series expansions into a table with $c$ the coefficients from the finite difference formula. Observe that Taylor series terms of even powers in $h$ cancel out, and those of odd powers from $-kh$ simply double those from $kh$ parts of the expansions. The power of $h$ multiplying $f^{\left(k\right)}$ is $h^{k-1}$. Observing and exploiting such symmetries reduces the number of calculations considerably.

   ${\displaystyle \begin{array}{llllllllll}& k& & & & 1& & 3& & 5\\ & \mathrm{term}& c& 2c& f^{\text{'}}\left(t\right)& 2c{f}^{\text{'}}\left(t\right)& f^{\text{'}\text{'}\text{'}}\left(t\right)& 2c{f}^{\text{'}\text{'}\text{'}}\left(t\right)& f^{\left(5\right)}\left(t\right)& 2c{f}^{\left(5\right)}\left(t\right)\\ & f(t+2h)& -\frac{1}{12}& -\frac{1}{6}& 2& -\frac{1}{3}& 8& -\frac{4}{3}& 32& -\frac{16}{3}\\ & f(t+h)& \frac{8}{12}& \frac{4}{3}& & \frac{4}{3}& 1& \frac{4}{3}& & \frac{4}{3}\\ \mathrm{Sum}& & & & & 1& & 0& & -4\\ \mathrm{Sum}/k!& & & & & 1& & 0& & -\frac{1}{30}\end{array}}$

   Deduce leading-order error

   ${\displaystyle {\epsilon }_1=-\frac{h^4{f}^{\left(5\right)}\left(\xi \right)}{30}.}$

   This can be verified in Mathematica.

   

   Set origin at $t=0$. Formula (1) contains data $𝒟=\{(kh,f_k),k=-2,-1,1,2\}\bigcup \{0,f_0^{\text{'}}\}$ with $f_k=f(kh)$. for a total of 5 conditions that can be satisfied by polynomial $p\left(t\right)$ of degree $n⩾4$.

   ${\displaystyle p(-2h)=f_{-2},p(-h)=f_{-1},p\left(h\right)=f_1,p\left(2h\right)=f_2,}$

   ${\displaystyle p^{\text{'}}\left(0\right)=f_0^{\text{'}}=\frac{1}{12h}[-f_2+8f_1-8f_{-1}+f_{-2}].}$

   This exercise highlights use of the Lagrange form of a Hermite interpolating polynomial with differing types of information at each node. The Lagrange basis functions

   ${\displaystyle a_i\left(t\right)=a_i\left(\alpha h\right)=[1-2(\alpha -i)h{\ell }_i^{\text{'}}(ih)]{\ell }_i^2(\alpha h),b_0\left(t\right)=b_0(\alpha h)=\alpha h{\ell }_0^2(\alpha h),}$

   ${\displaystyle {\ell }_i\left(t\right)={\ell }_i\left(\alpha h\right)=\prod _{k=-2,k\ne 0,i}^2\frac{\alpha h-kh}{ih-kh}=\prod _{k=-2,k\ne 0,i}^2\frac{\alpha -k}{i-k},i=-2,-1,1,2,}$

   ${\displaystyle {\ell }_0\left(t\right)={\ell }_0\left(\alpha h\right)=\prod _{k=-2,k\ne 0}^2\frac{\alpha h-kh}{(-kh)}=\frac{1}{4}({\alpha }^2-1)({\alpha }^2-2)}$

   satisfy the desired conditions leading to the polynomial

   ${\displaystyle p\left(t\right)=p\left(\alpha h\right)=f_0^{\text{'}}{b}_0(\alpha h)+\sum _{i=-2,i\ne 0}^2{f}_i{a}_i(\alpha h).}$

   A similar analysis can be applied to the second formula giving the error term

   ${\displaystyle {\epsilon }_2=-\frac{h^2{f}^{\left(3\right)}\left(\xi \right)}{3}.}$

   Steps for the convergence study:

   $\circ$Define the finite difference derivative approximations

   ∴	D1(t,f,h)=(-f(t+2*h)+8*f(t+h)-8*f(t-h)+f(t-2*h))/(12*h);

   ∴	D2(t,f,h)=(-f(t+2*h)+4*f(t+h)-3*f(t))/(2*h);

   ∴

   $\circ$Define the specified study functions

   ∴	f1(t)=sin(pi*t/4); f2(t)=exp(10*t); f3(t)=exp(-10*t);

   ∴

   $•$Define a function to construct the convergence plot by: evaluating the error

   ${\displaystyle u_k=\lg \left(e_k\right)=\lg |D_{h/2}f-D_{h}f|\cong p-q\lg h_k}$

   for $h_k=h_0{2}^{-k}$, $k=1,\dots ,N$, extracting the order of convergence $p$ by least squares (linear regression)

   ${\displaystyle 𝑨=\left[\begin{array}{ll}1& \lg h\end{array}\right]=\left[\begin{array}{ll}1& 1\\ 1& 2\\ ⋮& ⋮\\ 1& N\end{array}\right];{min}_{(p,q)}||𝑨\left[\begin{array}{l}p\\ q\end{array}\right]-𝒖||\Rightarrow \left[\begin{array}{l}p\\ q\end{array}\right]=𝑨\backslash 𝒖,}$

   and plotting the observed behavior.

   ∴

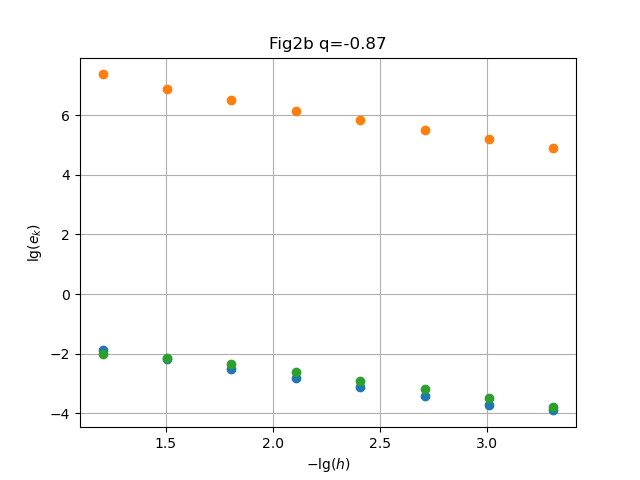
   function conv(h0,t,f,D,N,fname,figname) df=zeros(N+1,1); u=zeros(N,1); h=h0; lgh=zeros(N+1,1) for k=1:N+1 h=h/2; lgh[k]=log10(h); df[k]=D(t,f,h); end A=ones(N,2); x=-lgh[1:N]; A[:,2]=x; u[1:N]=log10.(abs.(df[2:N+1]-df[1:N])); q = floor((A\u)[2]*1000)/1000; plot(x,u,"o"); grid("on"); title(figname*" q="*string(q)) xlabel(L"$-\lg(h)$"); ylabel(L"\lg(e_k)") savefig(fname) return q end;

   ∴

   $•$

   Figure 1. Convergence study results. Top row for $f_1\left(t\right)=\sin (\pi t/4)$: (1a) Results exhibit loss of precision as $h$ decreases, and $q\cong -1$ is affected by error increase for small $h$; (1b) The first few step sizes after $h_0=1/8$ are not yet in the asymptotic regime, hence the observed order of convergence is $q=3.81$, less than the theoretical $𝒪\left(h^4\right)$ order. (1c) The asymptotic regime is reached at $h_0=1/32$, and the floating point precision is sufficient up to $h=h_0/2^4$ to obtain $q=3.94$, close to the theoretical order. Second row: (2a) Again for $h_0=1/32$ to $h=h_0/2^8$ the observed order for $f_2\left(t\right)=\exp \left(10t\right)$ is $q=3.9$, close to the theoretical prediction. The amplification of ${||f_2||}_{\infty }\approx e^{10}\approx 2.2\times {10}^4$ allows more accurate significant digits in floating point, but the overall precision is small (2b) The same $h$ range for $f_3$ with $||f_3||\approx 4\times {10}^{-5}$ not only achieves predicted order of accuracy, $q=3.97$, but also much better accuracy with machine precision $ϵ\approx {10}^{-16}$ achieved when $h=1/32/2^8\cong {10}^{-4}$. (2c) Second finite difference formula results for $f_1\left(•\right),f_2\left(•\right),f_3\left(•\right)$. The observed order of conergence is close to the theoretical $𝒪\left(h^2\right)$ in all cases, albeit with different overall errors.

   ∴	figdir=homedir()*"/courses/MATH661/homework/H08/";

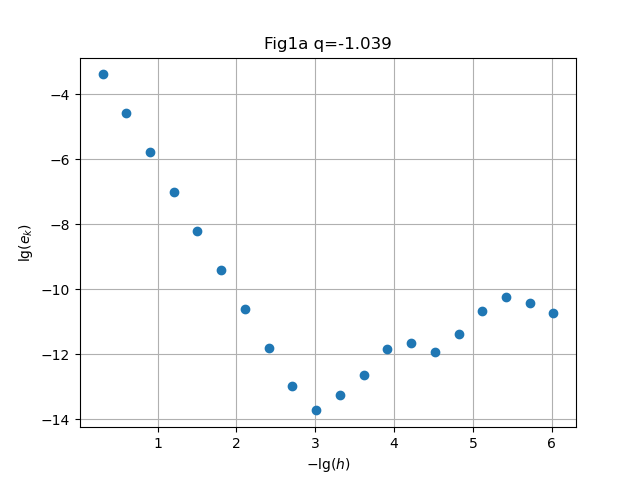
   ∴	clf(); h0=1; t0=1; conv(h0,t0,f1,D1,20,figdir*"H08Fig1a.png","Fig1a");

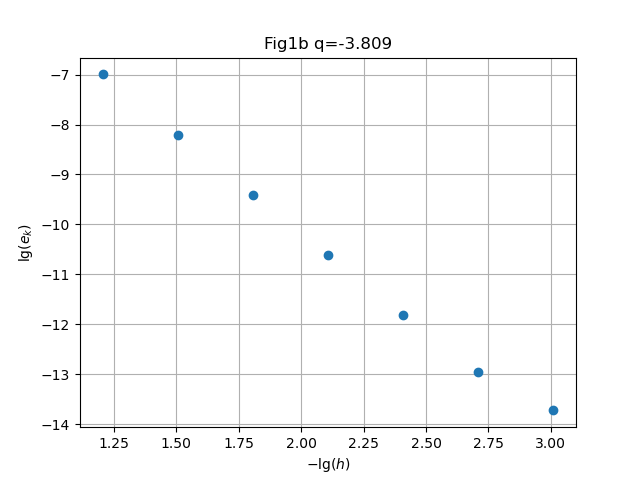
   ∴	clf(); h0=1/8; conv(h0,t0,f1,D1,7,figdir*"H08Fig1b.png","Fig1b");

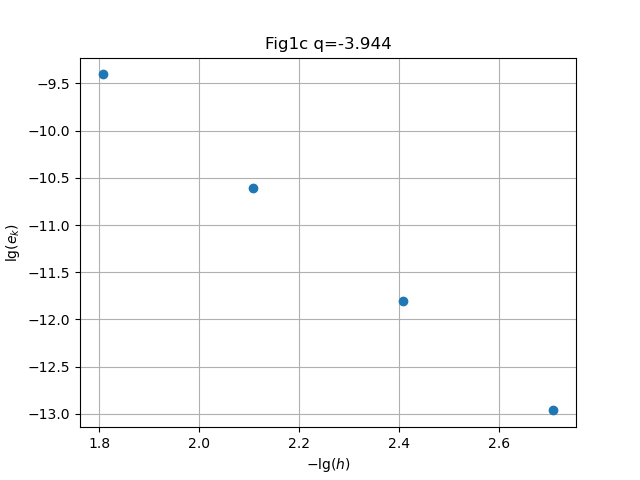
   ∴	clf(); h0=1/32; conv(h0,t0,f1,D1,4,figdir*"H08Fig1c.png","Fig1c");

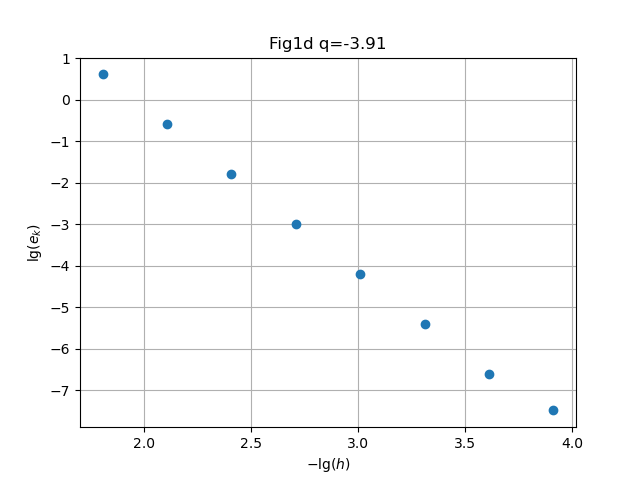
   ∴	clf(); h0=1/32; conv(h0,t0,f2,D1,8,figdir*"H08Fig1d.png","Fig1d");

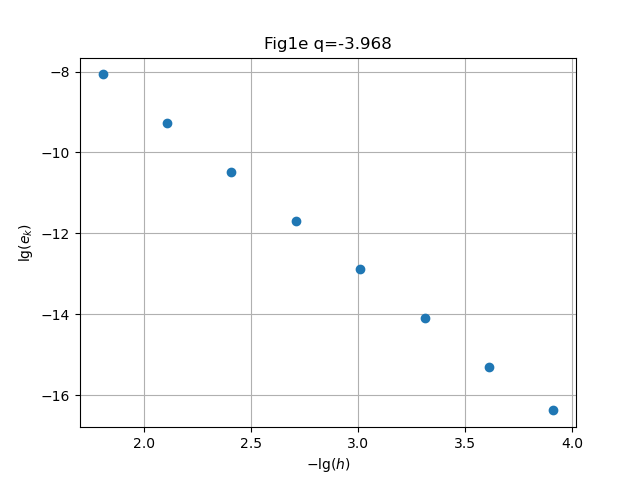
   ∴	clf(); h0=1/32; conv(h0,t0,f3,D1,8,figdir*"H08Fig1e.png","Fig1e");

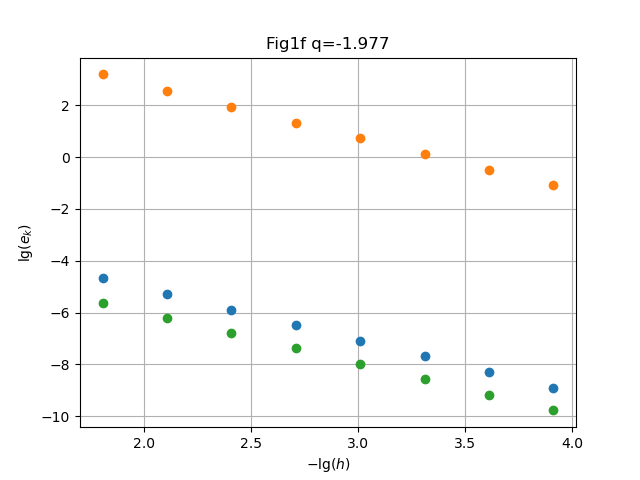
   ∴	clf(); h0=1/32; conv(h0,t0,f1,D2,8,figdir*"H08Fig1f.png","Fig1f");

   ∴	h0=1/32; conv(h0,t0,f2,D2,8,figdir*"H08Fig1f.png","Fig1f");

   ∴	h0=1/32; conv(h0,t0,f3,D2,8,figdir*"H08Fig1f.png","Fig1f");

   ∴

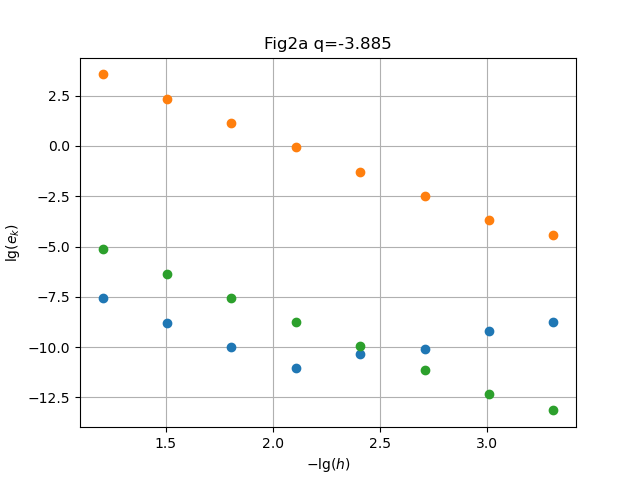
2. As above for

   ${\displaystyle f^{\text{'}\text{'}}\left(t\right)\cong \frac{1}{12h^2}[-f(t+2h)+16f(t+h)-30f\left(t\right)+16f(t-h)-f(t-2h)],}$ ${\displaystyle f^{\text{'}\text{'}\text{'}}\left(t\right)\cong \frac{1}{h^3}[f(t+3h)-3f(t+2h)+3f(t+h)-f\left(t\right)].}$

   Solution. Symbolic computation in Mathematica readily gives $𝒪\left(h^4\right)$, $𝒪\left(h^{}\right)$ behavior respectively.

   

   

   $\circ$Define the finite difference derivative approximations

   ∴	D3(t,f,h)=(-f(t+2*h)+16*f(t+h)-30*f(t)+16*f(t-h)-f(t-2*h))/(12*h^2);

   ∴	D4(t,f,h)=(f(t+3*h)-3*f(t+2h)+3*f(t+h)-f(t))/h^3;

   ∴

   $\circ$

   Figure 2. Convergence study results. Left: $f^{\text{'}\text{'}}$ formula results for $f_1\left(•\right),f_2\left(•\right),f_3\left(•\right)$, fourth order achieved for certain $h$ ranges. Right: $f^{\text{'}\text{'}\text{'}}$ formula results for $f_1\left(•\right),f_2\left(•\right),f_3\left(•\right)$, with $q\lesssim 1$

   ∴	figdir=homedir()*"/courses/MATH661/homework/H08/";

   ∴	clf(); h0=1/8; conv(h0,t0,f1,D3,8,figdir*"H08Fig2a.png","Fig2a");

   ∴	conv(h0,t0,f2,D3,8,figdir*"H08Fig2a.png","Fig2a");

   ∴	conv(h0,t0,f3,D3,8,figdir*"H08Fig2a.png","Fig2a");

   ∴	clf(); h0=1/8; conv(h0,t0,f1,D4,8,figdir*"H08Fig2b.png","Fig2b");

   ∴	conv(h0,t0,f2,D4,8,figdir*"H08Fig2b.png","Fig2b");

   ∴	conv(h0,t0,f3,D4,8,figdir*"H08Fig2b.png","Fig2b");

   ∴

3. Construct a recursive function RecInt(a,b,err,f,Q) that has arguments scalars $a,b,\mathrm{err}$ and functions $f,Q$ and approximates

   ${\displaystyle I\left(f\right)=\underset{a}{\overset{b}{\int }}f\left(t\right)dt}$

   through repeated application of quadrature rule $Q(f,a,b)$ according to the algorithm

   Algorithm

   Recursive quadrature

   RecInt(a,b,err,f,Q)

   $c=a+(b-a)/2$

   $Q_{\mathrm{ab}}=Q(f,a,b);Q_{\mathrm{ac}}=Q(f,a,c);Q_{\mathrm{cb}}=Q(f,c,b)$

   $e=|Q_{\mathrm{ac}}+Q_{\mathrm{cb}}-Q_{\mathrm{ab}}|/|Q_{\mathrm{ac}}+Q_{\mathrm{cb}}|$

   if $e<\mathrm{err}$

   return $Q_{\mathrm{ac}}+Q_{\mathrm{cb}}$

   else

   return RecInt(a,c,err,f,Q)+RecInt(c,b,err,f,Q)

   Test the recursive integration procedure with trapezoid, Simpson, and Gauss-Legendre rules of orders 2,3 on the integral

   ${\displaystyle \underset{-1}{\overset{1}{\int }}\cos \left(\frac{1}{t}\right).}$

   For each case, present plots of the integrand and the evaluation points used in the recursive quadrature algorithm. Construct convergence plots by executing the algorithm for various error thresholds ${\epsilon }_k$ and recording the number of evaluation points $n_k$. Plot $(\log n_k,\log {\epsilon }_k)$ and comment on whether the observed order of convergence is that predicted by theoretical quadrature error estimates.

   Solution. Define:

   $•$Recursive quadrature procedure

   ∴

   function RecInt(a,b,eps,f,Q,level) global nf,nmax,lmax c=a+(b-a)/2; Qab=Q(a,b,f); Qac=Q(a,c,f); Qcb=Q(c,b,f) new=Qac+Qcb; old=Qab; if nf > nmax/2 return new end if level > lmax return new end err=abs((new-old)/new) if err<eps return new else return RecInt(a,c,eps,f,Q,level+1)+RecInt(c,b,eps,f,Q,level+1) end end;

   ∴

   Quadrature rules:

   $•$Trapezoid

   ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(t\right)dt=\frac{b-a}{2}[f\left(a\right)+f\left(b\right)].}$

   ∴	function trapezoid(a,b,f) return 0.5*(b-a)*(f(a)+f(b)) end;

   ∴

   $•$Simpson

   ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(t\right)dt=\frac{b-a}{6}[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)].}$

   ∴	function simpson(a,b,f) return (b-a)/6 * (f(a)+4*f(0.5*(a+b))+f(b)) end;

   ∴

   $•$Gauss-Legendre 2

   ${\displaystyle \underset{-1}{\overset{1}{\int }}f\left(t\right)dt=f(-\sqrt{3})+f\left(\sqrt{3}\right).}$

   ∴	function gl2(a,b,f) s=(b-a)/2; z(t)=s*(t+1)+a; s3=sqrt(1/3); return s*(f(z(-s3))+f(z(s3))) end;

   ∴

   $•$Gauss-Legendre 3

   ${\displaystyle \underset{-1}{\overset{1}{\int }}f\left(t\right)dt=\frac{5}{9}f(-\sqrt{\frac{3}{5}})+\frac{8}{9}f\left(0\right)+\frac{5}{9}f\left(\sqrt{\frac{3}{5}}\right)}$

   ∴	function gl3(a,b,f) s=(b-a)/2; z(t)=s*(t+1)+a; s35=sqrt(3/5); w1=5/9; w0=8/9 return s*(w1*f(z(-s35)) + w0*f(z(0)) + w1*f(z(s35))) end;

   ∴

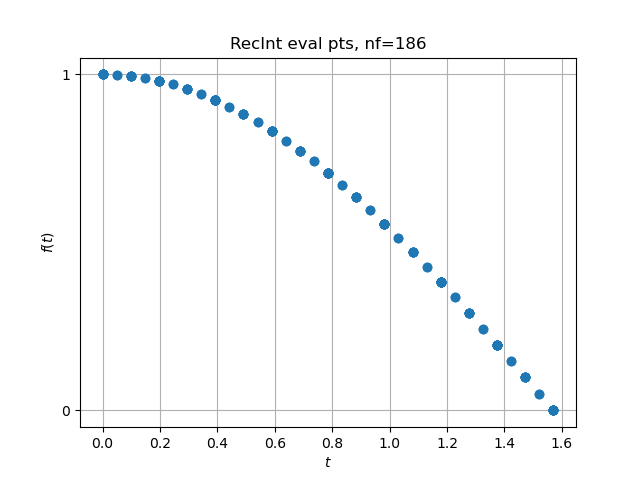
   $•$Define the integrand. Each time the integrand is called record the evaluation point and increment a counter of function evaluations. The integrand is singular at $t=0$, but over an interval of measure zero in the limit. Hence setting the integrand value to zero at $t=0$ does not affect the integral value. Also define a simpler integrand $g$ for overall testing.

   ∴	function f(t) global nf,tvals,fvals if abs(t)<1.0e-6 fval=0. else fval=cos(1/t) end nf = nf+1; tvals[nf]=t; fvals[nf]=fval return fval end;

   ∴	function g(t) global nf,tvals,fvals fval = cos(t) nf = nf+1; tvals[nf]=t; fvals[nf]=fval return fval end;

   ∴

   $\circ$Initialize function evaluation counter, values, call the routine for simple integrand

   ${\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \left(t\right)dt=1}$

   Figure 3. For integrand $g\left(t\right)=\cos \left(t\right)$ function evaluation points are close to an equidistant interval partition. Three accurate digits ($\epsilon <{10}^{-3}$) are attained with $n_f$=186,27,18,9 function evaluations, highlighting the effectiveness of high-order quadrature.

   ∴	global nf,nmax,lmax

   ∴	nf=0; nmax=100000; lmax=8; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(0,pi/2,10.0^(-3),g,trapezoid,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}186.0& 0.9997991943200188\end{array}\right]}$

   (3)

   ∴	clf(); plot(tvals[1:nf],fvals[1:nf],"o");

   ∴	xlabel(L"$t$"); ylabel(L"$f(t)$"); grid("on");

   ∴	title("RecInt eval pts, nf="*string(nf));

   ∴	figdir=homedir()*"/courses/MATH661/homework/H08/";

   ∴	savefig(figdir*"Fig3gT.png");

   ∴	nf=0; nmax=100000; lmax=8; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(0,pi/2,10.0^(-3),g,simpson,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}27.0& 1.0000082955239677\end{array}\right]}$

   (4)

   ∴	nf=0; nmax=100000; lmax=8; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(0,pi/2,10.0^(-3),g,gl2,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}18.0& 0.9999944679581385\end{array}\right]}$

   (5)

   ∴	nf=0; nmax=100000; lmax=8; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(0,pi/2,10.0^(-3),g,gl3,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}9.0& 1.000000118910998\end{array}\right]}$

   (6)

   ∴

   $186$

   ∴

   $•$Initialize function evaluation counter, values, call the routine for singular integrand

   ${\displaystyle \underset{1}{\overset{-1}{\int }}\cos (1/t)dt=2-\pi +\underset{0}{\overset{1}{\int }}\frac{\sin t}{t}dt\approx -0.1688}$

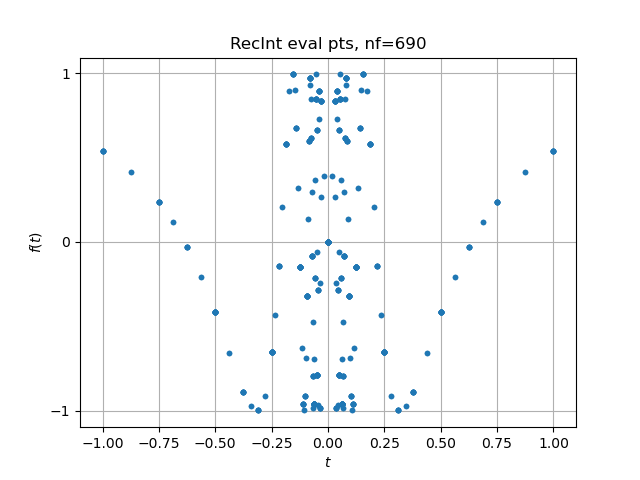   Figure 4. For integrand $f\left(t\right)=\cos (1/t)$ function evaluation points are clustered in regions of rapid variation of the function. Within a limit on the number of function evaluation $n_f\cong 5\times {10}^5$, only the GL3 quadrature gives a value of -0.16 with two accurate digits. This example highlights both recursive quadrature and the need for specialized numerical quadrature procedures for highly oscillatory or singular integrands.

   ∴	global nf,nmax,lmax

   ∴	nf=0; nmax=100000; lmax=8; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(-1,1,10.0^(-1),f,trapezoid,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}690.0& -0.14465818164911176\end{array}\right]}$

   (7)

   ∴	clf(); plot(tvals[1:nf],fvals[1:nf],".");

   ∴	xlabel(L"$t$"); ylabel(L"$f(t)$"); grid("on");

   ∴	title("RecInt eval pts, nf="*string(nf));

   ∴	figdir=homedir()*"/courses/MATH661/homework/H08/";

   ∴	savefig(figdir*"Fig3fT.png");

   ∴	nf=0; nmax=1000000; lmax=32; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(-1,1,10.0^(-2),f,trapezoid,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}500058.0& -0.1574321351531846\end{array}\right]}$

   (8)

   ∴	nf=0; nmax=1000000; lmax=32; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(-1,1,10.0^(-2),f,simpson,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}500067.0& -0.37476168010680994\end{array}\right]}$

   (9)

   ∴	nf=0; nmax=1000000; lmax=32; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(-1,1,10.0^(-2),f,gl2,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}500046.0& -0.4505206896512667\end{array}\right]}$

   (10)

   ∴	nf=0; nmax=1000000; lmax=32; tvals=zeros(nmax,1); fvals=zeros(nmax,1);

   ∴	Qg=RecInt(-1,1,10.0^(-2),f,gl3,0); [nf Qg]

   ${\displaystyle \left[\begin{array}{cc}500103.0& -0.16578576294469366\end{array}\right]}$

   (11)

   ∴

2Track 2

1. Use the finite difference expressions of the derivative

   ${\displaystyle \frac{d}{dt}=\frac{1}{h}(\Delta -\frac{1}{2}{\Delta }^2+\dots )=\frac{1}{h}(\nabla +\frac{1}{2}{\nabla }^2+\dots )=\frac{1}{h}(\delta -\frac{{\delta }^3}{24}+\cdots )}$

   to obtain the approximations.

   ${\displaystyle f^{\text{'}}\left(t\right)\cong \frac{1}{12h}[-f(t+2h)+8f(t+h)-8f(t-h)+f(t-2h)],}$ ${\displaystyle f^{\text{'}}\left(t\right)\cong \frac{1}{2h}[-3f\left(t\right)+4f(t+h)-f(t+2h)].}$

   Conduct a convergence study as $h\to 0$ for $f\left(t\right)\in \{\sin (\pi t/4),e^{10t},e^{-10t}\}$ at $t_0=1$, and compare the observed order of convergence with theoretical estimates. How do the three functions differ, and what effect does this have on derivative approximation?

   Solution. See Track 1 above for the standard convergence study. The Track 2 aspect of this exercise is to highlight how research problems arise.

   The results

   ${\displaystyle \frac{d}{dt}=\frac{1}{h}\ln (I+\Delta )=-\frac{1}{h}\ln (I-\nabla )=\frac{2}{h}\mathrm{arcsinh}\left(\frac{\delta }{2}\right),}$

   ${\displaystyle \Delta =E-I,\nabla =I-E^{-1},\delta =E^{1/2}-E^{-1/2}}$

   indicate multiple ways to express the differentiation operator $D=d/dt$ in terms of the translation operator $E$. One consideration in constructing finite difference approximations of a derivative is the number of function sample points, known as the stencil size. For example, a fourth order accurate formula is obtained with a stencil size of 5 from $hD=\ln (I+\Delta )$, using sample points $t+kh$, $k=0,1,\dots ,4.$ The formula

   ${\displaystyle \frac{d}{dt}f\left(t\right)\cong \frac{1}{12h}(-E^2+8E-8E^{-1}+E^2)f\left(t\right),}$

   is of fourth order accuracy, but has a stencil size of 4. This suggests exploring what additional expressions of $D$ in terms of functions of $E,\Delta ,\nabla ,\delta$ might be found. This is also the typical research scenario: when a result does not conform to known theory, seek extensions of the theory.

   Carry out calculations to obtain the requested approximation of the derivative in terms of finite differences

   ${\displaystyle D=\frac{d}{dt}=\frac{(E-E^{-1})}{12h}[8I-(E+E^{-1})]=\frac{1}{2}[\frac{1}{h}(\Delta -\frac{1}{6}{\Delta }^2)+\frac{1}{h}(\nabla +\frac{1}{6}{\nabla }^2)].}$

   This suggests an average of one-sided finite differences, truncated to first two terms,

   ${\displaystyle D=\frac{1}{2}(F+B),F=\frac{1}{h}(\Delta -\frac{1}{6}{\Delta }^2+\cdots ),B=\frac{1}{h}(\nabla +\frac{1}{6}{\nabla }^2+\cdots ).}$

   Take an additional research step and ask how the above may be extended. Can a function be found from the first few terms of its power series? Consider the following Mathematica result relevant for $hD=\ln (I-\nabla )$.

   The generating function has been found using only 4 terms. Extra credit (4 pts). Can you find generating functions for $F,B$?

2. As above for

   ${\displaystyle f^{\text{'}\text{'}}\left(t\right)\cong \frac{1}{12h^2}[-f(t+2h)+16f(t+h)-30f\left(t\right)+16f(t-h)-f(t-2h)],}$ ${\displaystyle f^{\text{'}\text{'}\text{'}}\left(t\right)\cong \frac{1}{h^3}[f(t+3h)-3f(t+2h)+3f(t+h)-f\left(t\right)].}$

   Use the series products

   ${\displaystyle \frac{d^2}{d{t}^2}=\frac{d}{dt}\frac{d}{dt}=\frac{1}{h^2}(\Delta -\frac{1}{2}{\Delta }^2+\dots )(\Delta -\frac{1}{2}{\Delta }^2+\dots ).}$

   Solution. As above.

3. Romberg integration is a combination of trapezoid quadrature over decreasing subintervals and Aitken extrapolation. Implement Romberg integration and test on

   ${\displaystyle \underset{0}{\overset{1}{\int }}{e}^t\cos (\pi t)dt.}$

   Present a convergence sutdy. What is the observed order of convergence?

   Solution.