MATH76109/21/2018

This is an example of using numerical methods to solve a realistic problem. The particular wave scattering problem considered here is linear and thus can be solved analytically using spherical harmonics. The solution is however quite complicated, and a numerical approach is often more effective.

Problem.

Wave scattering by an elastic sphere submerged in an incompressible fluid is described by the equation

${\displaystyle \rho {\partial }^2𝒖/\partial t^2=(\lambda +2\mu )\nabla (\nabla \cdot 𝒖)-\mu \nabla \times (\nabla \times 𝒖)}$

(1)

where:

• $𝒖(t,𝒙)$ is the displacement [m]

• $\rho$ is the density [kg/m${}^3$]

• $\lambda ,\mu$ are the bulk, shear elastic moduli [N/m${}^2$].

Elastic media sustain two types of waves:

• longitudinal or $P$-waves (pressure waves) with wave velocity $c_p=\sqrt{(\lambda +2\mu )/\rho }$

• transverse or $S$-waves (shear waves) with wave velocity $c_s=\sqrt{\mu /\rho }$

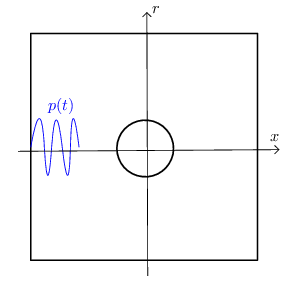
Consider a plane pressure wave $p\left(t\right)=P\sin \left(\omega t\right)$, $$entering a cube of side $a=8$m filled with water ($\rho =1000$ kg/m${}^3$, $c_p=1500$ m/s, $c_s=0$) containing a steel sphere of radius $r=1$m ($\rho =7700$ kg/m${}^3$, $c_p=6000$ m/s, $c_s=3200$ m/s) (Fig. 1)

Figure 1. Schematic of sphere scattering problem

${\displaystyle }$

1. Derive time evolution equations for the curl $𝛀=\nabla \times 𝒖$, and divergence $D=\nabla \cdot 𝒖$, first in vector form, and then in spherical coordinates assuming axisymmetry. What is the type of these equations? How many independent curl components arise in the axisymmetric case? (1pt)

2. Consider the Helmoholtz decomposition $𝒖=-\nabla \Psi +\nabla \times 𝑨$. Determine the time evolution equations for $\Psi ,𝑨$, again in vector and axisymmetric coordinate forms. As above, what is the type of the equations? How many independent components of the vector potential $𝑨$ arise in the axisymmetric case? (1pt)

3. Solve for $(D,𝛀)$ by:

   1. leap-frog

   2. Lax-Friedrichs

   3. upwind

   4. Lax-Wendroff

   Model the sphere by modification of the material properties ($\lambda ,\mu$). Carry out the time integration to allow both waves reflected by the sphere and those refracted by the sphere to leave the domain. Present convergence behavior for all schemes. (4 pts)

4. Solve for $(\Psi ,𝑨)$ by the same methods as above. Reconstruct $𝒖=-\nabla \Psi +\nabla \times 𝑨$, compute $(D,𝛀)$ and compare with solutions obtained from above at each considered grid resolution. (6 pts)

Remark.

1. Feel free to communicate with other students on approach to solve above problem, but draft the final report independently.

2. Draft your report by completing this file

3. The above tasks are impossible to solve within the allotted time without use of automation in generation of formulas, code, plots through utilities such as Mathematica, Gnuplot, make, Python. The appropriate techniques are shown in class. The homework requires you use these techniques on a different, but similar problem.

4. Start the homework immediately after it being posted. The homework requires assimilation of course theoretical and practical concepts and about 12-15 hours of effort during the two-week alloted time.

5. All results should be analyzed and commented. In particular, comment on whether numerical experiments conform to theoretical predictions.