MATH76108/24/2018

1TeXmacs

TeXmacs is an editor especially well suited for scientific work:

• Even more so than Emacs, TeXmacs can be extensively customized. Much of the editor is written in Scheme (a LISP descendent). Several customizations of TeXmacs have been carried out in SciComp@UNC.

• Mathematical text is easily written, in legible form, e.g. from the IBVP $q:[0,\infty )\times [0,1]\to ℝ$

  ${\displaystyle \{\begin{array}{l}{q}_t=q_{xx}\mathrm{in}(0,1)\\ q(t=0,x)=f\left(x\right)\mathrm{on}[0,1]\\ q(t,0)=g_0\left(t\right),q(t,1)=g_1\left(t\right)\end{array}.,}$

  (1)

  semidiscretization at nodes $x_i=ih$, $h=1$

• The text can be exported to LaTeX, HTML, PDF formats.

• Computations can be interspersed, such that one obtains a “living” document that contains the code used to produce results.

2Embedded sessions

The public-domain Linux environment encourages compatibility among conforming applications, such that they can work together to solve complex tasks. This approach is in marked contrast to closed-form commercial operating systems (Windows, macOS) and applications. Even commercial programs (e.g., Mathematica) that conform to standard Linux practices can work in concert with other applications.

Within SciComp@UNC, TeXmacs has been configured to embed sessions of other applications:

Asymptote

A general purpose vector graphics language

Asymptote]

size(5cm); for (int n = 3; n <= 7; ++n) { draw(shift(2.2*n, 0) * polygon(n));}

Asymptote]

Figure 1. Figure generated using folded Asymptote code

Eukleides

An environment for generation of geometrical figures

Eukleides]

box -1, -1, 7, 3 A B C isosceles H = projection(C, line(A, B)) draw (A.B.C) C.H dashed H end label A 180: B 0: C 90: B, H, C right B, A, C double C, B, A double A.H B.H A.C double C.B double end

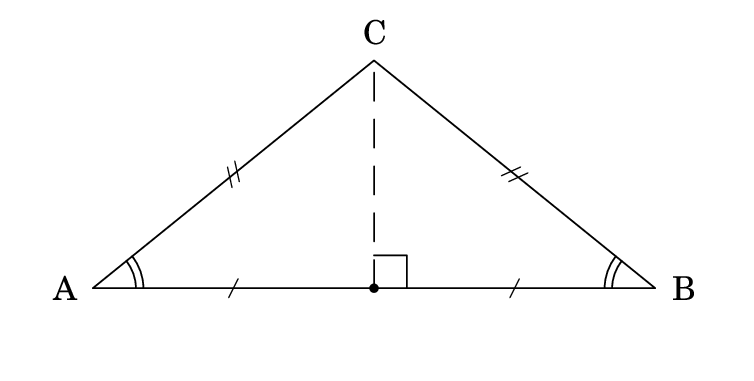
Eukleides]

Gnuplot

Gnuplot is graphics application

GNUplot]

plot sin(cos(x))+cos(sin(x))

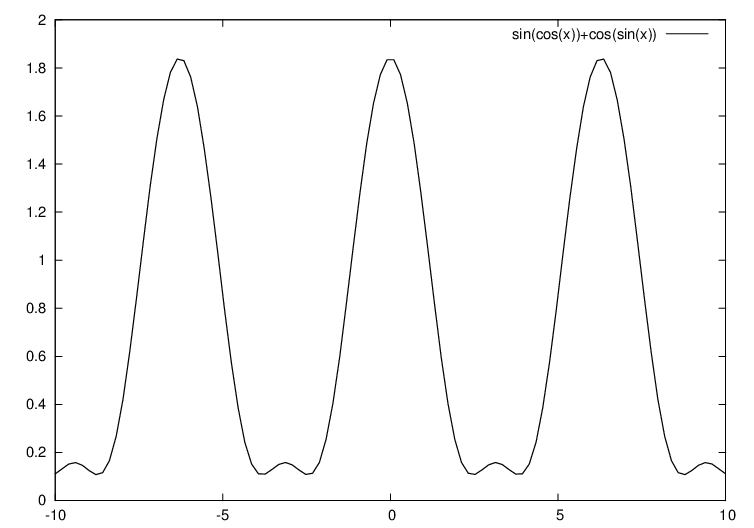
GNUplot]

Lisp

;; Loading file /opt/TeXmacs/plugins/lisp/clisp/clisp-init.lisp …
;;  Loading file lisp/tmlib.lisp …
;;  Loaded file lisp/tmlib.lisp

;; Loaded file /opt/TeXmacs/plugins/lisp/clisp/clisp-init.lisp

CLisp>

(car '(a b c))

A

CLisp>

(cdr '(a b c))

(B C)

CLisp>

Mathematica

Mathematica

In[1]:=

N[Pi,1000]

$3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420199$

In[2]:=

100!

${\displaystyle 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000}$

In[4]:=

D[Sin[Cos[x]]+Cos[Sin[x]],{x,10}]

${\displaystyle 945{\sin }^5\left(x\right)\sin (\sin \left(x\right))-2205{\sin }^3\left(x\right)\sin (\sin \left(x\right))+\sin \left(x\right)\sin (\sin \left(x\right))-945\cos (\cos \left(x\right)){\cos }^5\left(x\right)+2205\cos (\cos \left(x\right))\cos {}^3\left(x\right)-\cos (\cos \left(x\right))\cos \left(x\right)+{\cos }^{10}\left(x\right)(-\cos (\sin \left(x\right)))-120\cos {}^8\left(x\right)\cos (\sin \left(x\right))+45\sin \left(x\right)\sin (\sin \left(x\right)){\cos }^8\left(x\right)+630\sin {}^2\left(x\right){\cos }^6\left(x\right)\cos (\sin \left(x\right))-2352{\cos }^6\left(x\right)\cos (\sin \left(x\right))+2730\sin \left(x\right)\sin (\sin \left(x\right)){\cos }^6\left(x\right)-3150{\sin }^3\left(x\right)\sin (\sin \left(x\right))\cos {}^4\left(x\right)+15750{\sin }^2\left(x\right){\cos }^4\left(x\right)\cos (\sin \left(x\right))-4725{\sin }^2\left(x\right)\cos {}^4\left(x\right)\sin (\cos \left(x\right))-5440{\cos }^4\left(x\right)\cos (\sin \left(x\right))-3150{\cos }^4\left(x\right)\sin (\cos \left(x\right))+19530\sin \left(x\right)\sin (\sin \left(x\right)){\cos }^4\left(x\right)+3150{\sin }^4\left(x\right)\cos (\cos \left(x\right)){\cos }^3\left(x\right)+22050{\sin }^2\left(x\right)\cos (\cos \left(x\right))\cos {}^3\left(x\right)+630{\sin }^6\left(x\right){\cos }^2\left(x\right)\sin (\cos \left(x\right))-4725{\sin }^4\left(x\right)\cos {}^2\left(x\right)\cos (\sin \left(x\right))+15750{\sin }^4\left(x\right){\cos }^2\left(x\right)\sin (\cos \left(x\right))-22050{\sin }^3\left(x\right)\sin (\sin \left(x\right)){\cos }^2\left(x\right)+25515{\sin }^2\left(x\right){\cos }^2\left(x\right)\cos (\sin \left(x\right))+25515{\sin }^2\left(x\right){\cos }^2\left(x\right)\sin (\cos \left(x\right))-256{\cos }^2\left(x\right)\cos (\sin \left(x\right))+255{\cos }^2\left(x\right)\sin (\cos \left(x\right))+7125\sin \left(x\right)\sin (\sin \left(x\right)){\cos }^2\left(x\right)-{\sin }^{10}\left(x\right)\sin (\cos \left(x\right))-45{\sin }^8\left(x\right)\cos (\cos \left(x\right))\cos \left(x\right)-120{\sin }^8\left(x\right)\sin (\cos \left(x\right))-2730{\sin }^6\left(x\right)\cos (\cos \left(x\right))\cos \left(x\right)-2352{\sin }^6\left(x\right)\sin (\cos \left(x\right))-19530{\sin }^4\left(x\right)\cos (\cos \left(x\right))\cos \left(x\right)-3150{\sin }^4\left(x\right)\cos (\sin \left(x\right))-5440{\sin }^4\left(x\right)\sin (\cos \left(x\right))-7125{\sin }^2\left(x\right)\cos (\cos \left(x\right))\cos \left(x\right)+255{\sin }^2\left(x\right)\cos (\sin \left(x\right))-256{\sin }^2\left(x\right)\sin (\cos \left(x\right))}$

In[5]:=

1 == 2

${\displaystyle \text{False}}$

In[6]:=

1 == 1

${\displaystyle \text{True}}$

In[7]:=

Eq = x==1

${\displaystyle x=1}$

In[8]:=

Eq /. x->1

${\displaystyle \text{True}}$

In[9]:=

ODE = y'[x] + x y[x] == Sin[x]

${\displaystyle y^{\text{'}}\left(x\right)+xy\left(x\right)=\sin \left(x\right)}$

In[14]:=

sol = DSolve[ODE,y[x],x]

${\displaystyle \left\{\{y\left(x\right)\to c_1{e}^{-\frac{x^2}{2}}-\frac{1}{2}i\sqrt{\frac{\pi }{2}}{e}^{\frac{1}{2}-\frac{x^2}{2}}(\text{erfi}\left(\frac{x+i}{\sqrt{2}}\right)-\text{erfi}(\frac{}{x-i}\sqrt{2}))\}\right\}}$

In[17]:=

z[x_] = y[x] /. sol[[1,1]]

${\displaystyle c_1{e}^{-\frac{x^2}{2}}-\frac{1}{2}i\sqrt{\frac{\pi }{2}}{e}^{\frac{1}{2}-\frac{x^2}{2}}(\text{erfi}\left(\frac{x+i}{\sqrt{2}}\right)-\text{erfi}(\frac{}{x-i}\sqrt{2}))}$

In[15]:=

sol[[1,1]]

${\displaystyle y\left(x\right)\to c_1{e}^{-\frac{x^2}{2}}-\frac{1}{2}i\sqrt{\frac{\pi }{2}}{e}^{\frac{1}{2}-\frac{x^2}{2}}(\text{erfi}\left(\frac{x+i}{\sqrt{2}}\right)-\text{erfi}(\frac{}{x-i}\sqrt{2}))}$

In[18]:=

z[1.]

${\displaystyle 0.606531c_1+(1.21479+0.i)}$

In[19]:=

Maxima

(%i1)

diff(sin(x),x);

${\displaystyle \text{(\%o1)}\cos \left(x\right)}$

(%i2)

Octave

${\displaystyle A={\displaystyle \left(\begin{array}{ccc}0.45229& 0.22986& 0.70938\\ 0.65207& 0.84622& 0.8479\\ 0.28058& 0.5938& 0.36148\end{array}\right)},A^{-1}={\displaystyle \left(\begin{array}{ccc}-11.373& 19.462& -23.333\\ 0.12663& -2.0461& 4.5509\\ 8.6198& -11.746& 13.402\end{array}\right)}}$

octave>

A=rand(3)

${\displaystyle \left(\begin{array}{ccc}0.93125& 0.050603& 0.82831\\ 0.22199& 0.11851& 0.75259\\ 0.09635& 0.24193& 0.66373\end{array}\right)}$

octave>

inv(A)

${\displaystyle \left(\begin{array}{ccc}1.5894& -2.5636& 0.9233\\ 1.15& -8.273& 7.9454\\ -0.6499& 3.3876& -1.5235\end{array}\right)}$

octave>

Python

Python]

from pylab import *

Python]

x=arange(0.,3.15,0.01); y=sin(x); plot(x,y);

Python]

show()

None

Python]

Shell

Shell session inside TeXmacs pid = 26400

Shell]

pwd

/home/student

Shell]

ls

bearclaw documents ecss0.log mitran-web research Wolfram Mathematica

courses   Downloads  fontconfig  perl5       TeXmacs

Desktop ecbx0.log mitran projects tmp

Shell]